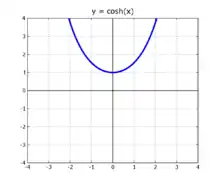
雙曲餘弦
在數學中,雙曲餘弦是一種雙曲函數,是雙曲幾何中,與歐幾里得幾何的餘弦函數相對應的函數。雙曲餘弦一般以cosh表示[1],在部分較舊的文獻中有時會以表示。[2]雙曲餘弦可以用來描述悬链线,即兩端固定自然下垂的繩索,因此可以用於進行悬索桥的工程計算。
 | |
| 性質 | |
| 奇偶性 | 偶 |
| 定義域 | (-∞,∞) |
| 到達域 | [1,∞) |
| 特定值 | |
| 當x=0 | 1 |
| 當x=+∞ | +∞ |
| 當x=-∞ | +∞ |
| 最大值 | +∞ |
| 最小值 | 1 |
| 其他性質 | |
| 渐近线 | 無 |
| 根 | 無實根 見雙曲餘弦#根一節 |
| 臨界點 | 0 |
| 拐點 | 無 |
| 不動點 | 無 |
定義
雙曲餘弦一般記為[3](有時會簡寫為[4]),其在複分析中定義為:
其中是複變指數函數。
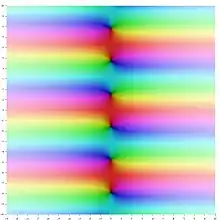 複數域雙曲餘弦的色相環複變函數圖形
複數域雙曲餘弦的色相環複變函數圖形
也就是說,雙曲餘弦可以視為指數函數與其倒數的算術平均數[5],即雙曲餘弦為自然指數函數的偶函數部分[6]。
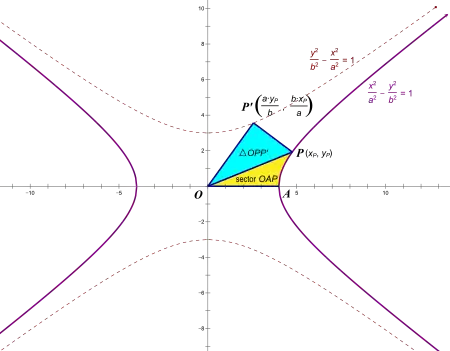
在雙曲幾何中,雙曲餘弦函數類似於歐幾里得幾何中的餘弦函數。一般的餘弦可以表示為單位圓上特定角的終邊正向與圓之交點的x座標;而雙曲餘弦則代表單位雙曲線上特定雙曲角的終邊正向與單位雙曲線之交點的x座標[7]。 對於非單位雙曲線的情形,如以下列形式定義的雙曲線:
令為雙曲角的終邊與雙曲線的交點,並令為點在共軛雙曲線上對應的點:
此時雙曲角可以透過交點 、共軛點與原點構成的三角形(三角形)與雙曲扇形的面積比來定義[7]:
在這個定義下,雙曲餘弦為雙曲角的終邊正向與單位雙曲線之交點的x座標除以雙曲線方程係數的結果[7]:
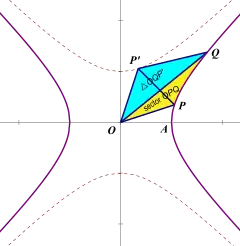
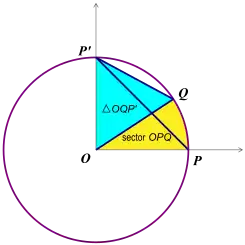
此外,亦可以透過三角形面積比來定義雙曲餘弦。若右圖(a)中雙曲角QOP 定義為[7]:
則其雙曲餘弦為[7]:
這個定義對應到單位圓上則可以定義一般的餘弦函數。若右圖(b)中角QOP 定義為[7]:
性質
雙曲餘弦在實數域中是連續函數,在複數域中是全純函數,因此在整個複數域中雙曲餘弦處處可微,其導函數為雙曲正弦函數。雙曲餘弦是偶函數,這意味著,雙曲餘弦滿足以下等式[8]:
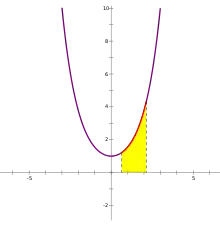
雙曲餘弦曲線下的面積(在有限區間內)總是等於該區間對應的弧長:[9]
由歐拉公式 和雙曲函數與指數函數的關聯能推出雙曲餘弦與餘弦的關係:
根
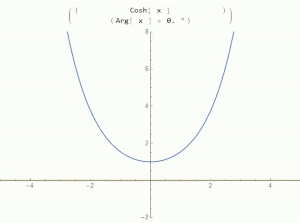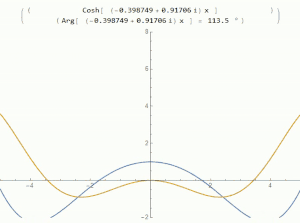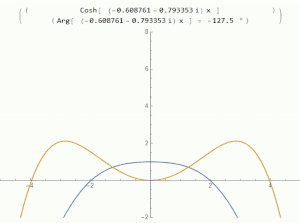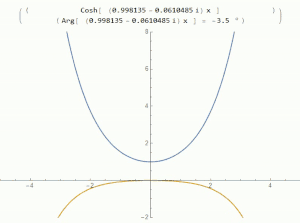
函數的根代表函數值為0的點[11]。雙曲餘弦函數的根可透過求解下列方程得到:
在實數域中,雙曲餘弦的最小值為1,不與x軸相交,因此上述方程無實根[8]。
而在複數域中可以找到雙曲餘弦的根。所有雙曲餘弦為零的點都是純虛數[12]:
原因是,若將表示成,其中皆為實數,則由有:
例如:[12]
用途
物理學
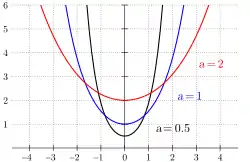
雙曲餘弦可以用來描述懸鏈線。懸鏈線在物理學中,可以用於描繪軟繩位於水平兩點間,在鉛直方向均勻受力下自然形變後的形狀。[13][14]其可以表示為:[15]
其中,為繩子的高度,繩子的最低點定為y軸()[16],是一個常數,由繩子本身性質(如密度)、與懸鏈線懸掛的方式決定,通常可以表示為,其中是重力加速度、是繩子的密度、為繩子上每一點處張力的水平分量。[17]
建築學
雙曲餘弦在建築學與工程學中一般用於計算懸索橋工程產生的懸鏈線。安东尼·高迪是最早將雙曲餘弦曲線融入建築設計的建築師之一[19],例如其作品聖家堂以及科洛尼亚桂尔教堂就有用到。
美國密蘇里州聖路易的聖路易斯拱門是一個倒過來的雙曲餘弦曲線外型的建築物。該拱門的最高點離地面約192公尺,其拱頂近似於以下方程:[20]
其中表示單位為公尺,且滿足公尺。而具體的幾何結構由結構工程師漢斯卡爾·班德爾提供給埃罗·萨里宁的數學方程確定。[21]
- ,
其中,常量為 68.7672英尺(21米)、常數為;625.0925英尺(191米)為質心的最高點、1,262.6651 sq ft(117 m2)為截面積的最大值(在拱底取到)、125.1406 sq ft(12 m2)為截面積的最小值(在拱頂取到)、299.2239英尺(91米)質心位於拱底之寬度的一半。[21]
參考文獻
- (1999) Collins Concise Dictionary, 4th edition, HarperCollins, Glasgow, ISBN 0 00 472257 4, p. 1386
- Dr. Franz Brzoska, Walter Bartsch, Mathematische Formelsammlung. 2. verbesserte, Fachbuchverlag Leipzig. 1956 (德文)
- . International Organization for Standardization. [1 July 2010]. (原始内容存档于2014-03-26).
- Gradshteyn, Izrail Solomonovich; Ryzhik, Iosif Moiseevich. 6. Academic Press, Inc.. 2000. ISBN 978-0-12-294757-5.
- . mathworks. [2021-07-11]. (原始内容存档于2021-07-12).
- Richard Hensh. (PDF). math.msu.edu. [2021-07-11]. (原始内容存档 (PDF)于2021-07-11).
- Mellen W. Haskell, "On the introduction of the notion of hyperbolic functions", 美國數學會快報 1:6:155–9, full text (页面存档备份,存于)
- (PDF). mathcentre.ac.uk. [2021-07-11]. (原始内容存档 (PDF)于2021-01-19).
- N.P., Bali. . Firewall Media. 2005: 472 [2021-07-11]. ISBN 81-7008-169-6. (原始内容存档于2021-07-11).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- . Math Vault. 2019-08-01 [2019-12-15]. (原始内容存档于2020-02-28) (美国英语).
- (PDF). wolfram.com. [2021-07-11]. (原始内容存档 (PDF)于2021-07-11).
- Kabai, Sándor; Tóth, János. . Wolfram Demonstrations Project. [December 14, 2010]. (原始内容存档于2021-02-24).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Lockwood, E.H. . . Cambridge. 1961: 122.
- Weisstein, Eric W. Catenary. MathWorld[14], 引文:「The parametric equations for the catenary are given by x(t) = t, y(t) = [...] a cosh(t/a), where t=0 corresponds to the vertex [...]」
- Routh, Edward John. . . University Press. 1891: 315 [2021-07-11]. (原始内容存档于2021-04-13).
- Osserman, Robert. (PDF). Notices of the American Mathematical Society. February 2010, 57 (2): 220–229 [2021-07-11]. ISSN 0002-9920. (原始内容 (PDF)存档于2012-10-23).
- Saudi, Antoni. . Casanova, Rossend (编). . Barcelona: Planeta. 2002: 168. ISBN 978-84-08-04332-4 (加泰罗尼亚语).
- (PDF). fac.ksu.edu.sa. [2021-07-11]. (原始内容存档 (PDF)于2021-07-11).
- . National Park Service. [December 14, 2010]. (原始内容存档于2011-04-13).