史特芬十四面體
史特芬十四面體是一種彈性多面體,由克勞斯·史特芬於1978年發現[1][2]:244-247[3]。這種多面體基於布里卡爾八面體但沒有自相交的面[4]。這個多面體一共有14個三角形面,是最簡單的由非相交面組成的彈性多面體。[5]其遵循強風箱猜想(strong bellows conjecture),這意味著其登不變量在形變過程皆保持不變。[6]
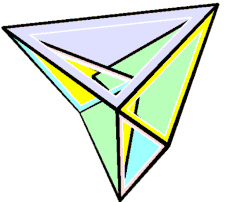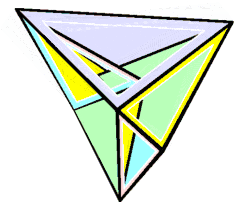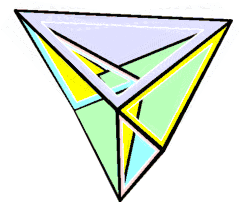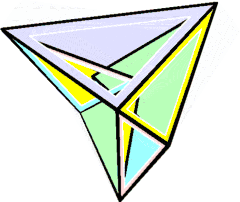 可局部活動的史特芬十四面體 | ||
| 類別 | 彈性多面體 | |
|---|---|---|
| 對偶多面體 | (未知) | |
| 性質 | ||
| 面 | 14 | |
| 邊 | 21 | |
| 頂點 | 9 | |
| 歐拉特徵數 | F=14, E=21, V=9 (χ=2) | |
| 組成與佈局 | ||
| 面的種類 | 14個三角形 | |
| 特性 | ||
| 彈性 | ||
| 圖像 | ||
| ||
性質
史特芬十四面體由14個面、21條邊和9個頂點組成。其6個面又可以分成2個子群:來自布里卡爾八面體的6個三角形組,以及將這些三角形組拼起來的另外兩個三角形。[7]
參見
參考文獻
- Lijingjiao; et al. (PDF). 2015 [2021-09-09]. (原始内容存档 (PDF)于2020-02-15).
- Cromwell, P. R. . New York: Cambridge University Press. 1997. ISBN 978-0521664059.
- Mackenzie, Dana. . Science (American Association for the Advancement of Science). 1998, 279 (5357): 1637–1637.
- Connelly, Robert, , Klarner, David A. (编), , Springer: 79–89, 1981, ISBN 978-1-4684-6688-1, doi:10.1007/978-1-4684-6686-7_10.
- Demaine, Erik D.; O'Rourke, Joseph, , , Cambridge University Press, Cambridge: 345–348, 2007, ISBN 978-0-521-85757-4, MR 2354878, doi:10.1017/CBO9780511735172
- Alexandrov, Victor, , Journal of Geometry, 2010, 99 (1-2): 1–13, MR 2823098, arXiv:0901.2989
 , doi:10.1007/s00022-011-0061-7.
, doi:10.1007/s00022-011-0061-7. - Fuchs, Dmitry; Tabachnikov, Serge, , Providence, RI: American Mathematical Society: 354, 2007 [2021-09-09], ISBN 978-0-8218-4316-1, MR 2350979, doi:10.1090/mbk/046, (原始内容存档于2017-03-03).
- Mark McClure. (PDF). marksmath.org. [2021-09-09]. (原始内容存档 (PDF)于2021-10-06).
- Gaĭfullin, A. A.; Ignashchenko, L. S., , Trudy Matematicheskogo Instituta Imeni V. A. Steklova, 2018, 302 (Topologiya i Fizika): 143–160, ISBN 5-7846-0147-4, MR 3894642, doi:10.1134/S0371968518030068
- Demaine, Erik D.; O'Rourke, Joseph, , , Cambridge University Press, Cambridge: 345–348, 2007, ISBN 978-0-521-85757-4, MR 2354878, doi:10.1017/CBO9780511735172
外部連結
- Steffen's Polyhedron (页面存档备份,存于), Greg Egan
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
