四角六片四角孔扭歪無限面體
在幾何學中,四角六片四角孔扭歪無限面體(日语:)[1]是一種正扭歪無限面體,由考克斯特和皮特里於1926年時發現[2][3],並命名為多立方體(英語:)[4]。其對偶多面體為六角四片四角孔扭歪無限面體[5]。
 () | ||||
| 類別 | 正扭歪無限面體 | |||
|---|---|---|---|---|
| 對偶多面體 | 六角四片四角孔扭歪無限面體 | |||
| 識別 | ||||
| 鮑爾斯縮寫 | muc | |||
| 數學表示法 | ||||
| 考克斯特符號 | ||||
| 施萊夫利符號 | {4,6|4} | |||
| 性質 | ||||
| 面 | 無限個正方形 | |||
| 邊 | 無限 | |||
| 頂點 | 無限 6個正方形的公共頂點 | |||
| 組成與佈局 | ||||
| 頂點圖 | 扭歪六邊形 {3}#{ } | |||
| 頂點佈局 | 同於立方體堆砌 | |||
| 特性 | ||||
| 扭歪、 點可遞 | ||||
| 圖像 | ||||
| ||||
四角六片四角孔扭歪無限面體是一種扭歪正多面體,可以看做是立方體的空間填充形式——立方體堆砌少去部分正方形面的結果[6]。
性質
四角六片四角孔扭歪無限面體由無限個正方形組成,每個頂點都是6個正方形的公共頂點,在頂點圖中為一個扭歪六邊形,此扭歪六邊形可以視為正八面體的皮特里多邊形,為下圖中的黑線部分。
四角六片四角孔扭歪無限面體由無限個正方形組成,並且在中間形成正方形的孔洞,在施萊夫利符號中計為{4,6|4},第一個4表示其由正方形構成,6表示每個頂點都是6個正方形的公共頂點,第二個4表示幾何體中間有正方形的孔洞。其對偶多面體為六角四片四角孔扭歪無限面體,施萊夫利符號中計為{6,4|4}。
相關多面體與鑲嵌
四角六片四角孔扭歪無限面體是三種正扭歪無限面體之一,另外兩種為:
| 图像 |  四角六片四角孔扭歪無限面體 |
 六角四片四角孔扭歪無限面體 |
 六角六片三角孔扭歪無限面體 |
|---|---|---|---|
| 施萊夫利符號 | {4,6|4} | {6,4|4} | {6,6|3} |
四角六片四角孔扭歪無限面體在拓樸中相當於六階正方形鑲嵌(施萊夫利符號:{4,6})的商空間,將四角六片四角孔扭歪無限面體中的結構進行拓樸變形可以構成一個六階正方形鑲嵌。
其他四角扭歪無限面體
有些扭歪無限面體也是由正方形組成的,例如四角六片五角孔扭歪無限面體。
四角六片五角孔扭歪無限面體
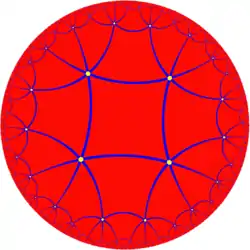
在幾何學中,四角六片五角孔扭歪無限面體(日语:)是一種位於雙曲緊湊空間的正扭歪無限面體。其在施萊夫利符號中計為{4,6|5},表示每個頂點都是6個正方形的公共頂點,並且具有正五邊形的孔洞。
四角六片五角孔扭歪無限面體於1967年時由C. W. L. Garner發現[7],可看作是由截半五階十二面體堆砌()移除所有正五邊形面來構造。
四角六片五角孔扭歪無限面體的對偶多面體為六角四片五角孔扭歪無限面體,與其相同頂點布局的堆砌體為過截角五階十二面體堆砌()。
四角五片扭歪無限面體
在幾何學中,四角五片扭歪無限面體(日语:)是指具有每個頂點都是五個正方形的公共頂點的扭歪多面體[3],有兩種形式,其具有的空間群在考克斯特記號中分別計為和[8][9]。
| 图像 | 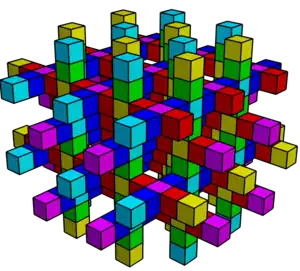 |
|
|---|---|---|
| 頂點附近的面 |  |
 |
有限的扭歪多面體
扭歪多面體是指面與頂點並不存在同一個三維空間而無法確定體積的多面體,除了扭歪無限面體是退化的情況外,有限面的扭歪多面體僅能存在於四維或以上的空間。
四維空間
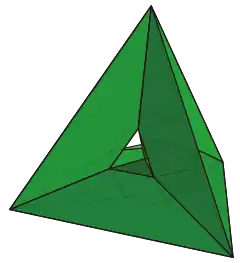
在四維空間中,有部分由正方形組成的扭歪多面體,例如:四角六片三角孔扭歪正三十面體{4,6|3}
四角六片三角孔扭歪正三十面體
 (施萊格爾投影) | ||
| 類別 | 扭歪正多面體 | |
|---|---|---|
| 數學表示法 | ||
| 施萊夫利符號 | {4,6|3} | |
| 性質 | ||
| 面 | 30 | |
| 邊 | 60 | |
| 頂點 | 20 | |
| 歐拉特徵數 | F=30, E=60, V=20 (χ=-10) | |
| 組成與佈局 | ||
| 頂點圖 | 扭歪六邊形 {3}#{ } | |
| 頂點佈局 | 同於截半五胞體 | |
| 特性 | ||
| 扭歪, 點可遞 | ||
| 圖像 | ||
| ||
在幾何學中,四角六片三角孔扭歪正三十面體(日语:)是一種位於四維空間的正扭歪多面體。其在施萊夫利符號中計為{4,6|3},表示每個頂點都是6個正方形的公共頂點,並且具有正三角形的孔洞。
四角六片三角孔扭歪正三十面體由30個面、60條邊和20個頂點組成,可以看做是截半五胞體去除所有正三角形面的結果,因此與截半五胞體共用相同的頂點布局。[10] 四角六片三角孔扭歪正三十面體的對偶多面體為六角四片三角孔扭歪正二十面體,由20個正六邊形組成。
性質
四角六片三角孔扭歪正三十面體由30個正方形組成,每個頂點都是6個正方形的公共頂點,在頂點圖中可以用46來表示,並且可以視為六階正方形鑲嵌的商空間。
- 體積與表面積
扭歪多面體不存在一個唯一的空間區域,就如同扭歪多邊形(不共面多邊形)無法找到一個唯一的多邊形內部區域一樣,因此四角六片三角孔扭歪正三十面體的體積不存在,但仍可以求表面積,其表面積為30個正方形面的面積,即32倍的邊長平方。
- 結構
| 四角六片三角孔扭歪正三十面體 | 截半五胞體 |
|---|---|
 |
 |
| 施萊格爾投影 | |
四角六片三角孔扭歪正三十面體的結構為S5群,其對稱群在考克斯特符號中可以用[[3,3,3]+]表示,且階數為60,並且與截半五胞體共用相同的頂點布局。
四角四片多角孔扭歪正多面體

由正方形組成且每個頂點都是4個正方形的公共頂點的扭歪多面體是一個無窮集合,其孔洞可以是任意多邊形,其可以從四維柱體柱構造。[11]
| 名稱 | 四角四片三角孔 扭歪正九面體 |
四角四片四角孔 扭歪正十六面體 |
四角四片五角孔 扭歪正二十五面體 |
四角四片六角孔 扭歪正三十六面體 |
四角四片n角孔 扭歪正n2面體 |
|---|---|---|---|---|---|
| 圖像 |  |
 |
|||
| 面 | 9 | 16 | 25 | 36 | n2 |
| 邊 | 18 | 32 | 50 | 72 | 2n2 |
| 頂點 | 9 | 16 | 25 | 36 | n2 |
| 歐拉特徵數 | 0(虧格=1) | 0(虧格=1) | 0(虧格=1) | 0(虧格=1) | 0(虧格=1) |
| 相同 頂點布局 的形狀 |
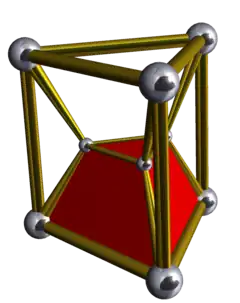 三角三角柱體柱 |
 超立方體 |
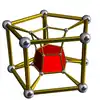 五角五角柱體柱 |
 六角六角柱體柱 |
 n角n角柱體柱 (n-n duoprism) |
參考文獻
- Petrie–Coxeter Maps Revisited(页面存档备份,存于) PDF, Isabel Hubard, Egon Schulte, Asia Ivic Weiss, 2005
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5,
- Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 (页面存档备份,存于)
- (Paper 2) H.S.M. Coxeter, "The Regular Sponges, or Skew Polyhedra", Scripta Mathematica 6 (1939) 240–244.
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.)
- . Tokai library. 東海大学出版会. 2002 [2018-09-02]. ISBN 9784486015871. (原始内容存档于2018-09-02).
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
- . . geocities.jp. [2018-09-02]. (原始内容存档于2018-10-08).
- The Symmetry of Things, 2008, Chapter 23 Objects with Primary Symmmetry, Infinite Platonic Polyhedra, pp. 333–335
- kotetu. . eonet.ne.jp. 2017-03-31 [2018-09-02]. (原始内容存档于2017-08-13).
- 正多面体を解く2002 [1] 第6章 ねじれ正多面体:ねじれ多面体の具体的構成法
- Garner, C. W. L. Regular Skew Polyhedra in Hyperbolic Three-Space. Canad. J. Math. 19, 1179–1186, 1967. (页面存档备份,存于) Note: His paper says there are 32, but one is self-dual, leaving 31.
- J. R. Gott, Pseudopolyhedrons, American Mathematical Monthly, Vol 74, p. 497-504, 1967.
- The Symmetries of things, Pseudo-platonic polyhedra, p.340-344
- Klitzing, Richard. . bendwavy.org.
- Klitzing, Richard. . bendwavy.org.