拿破崙問題
拿破崙問題(Napoleon's problem)是著名的圓規作圖問題,原題如下:
給定一圓和其圓心,只用圓規將此圓四等分。(此圓指的是圓周而不是圓面積)
此題目是由義大利數學家洛倫佐·馬斯凱羅尼向拿破崙·波拿巴提出的問題,但我們不知道他是否有解出這個問題。此題目後來又更加進化,變成只給定一圓,只用圓規將此圓四等分,在這種情況必須先用圓規作圖找到圓心。以上兩種都被稱為拿破崙問題。
找出圓心
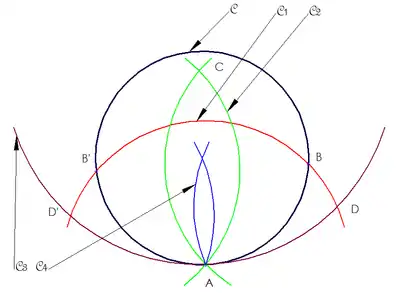
→深藍、→紅、→綠、→紫、→藍
作法
四等分圓

作法
由前面我們已經知道圓心的位置
- 在已知的圓上找任意一點 ,以為半徑畫弧 ,交圓於 、 兩點。
- 以 為圓心,為半徑畫弧 ,交圓於 点(和 點)。
- (继续分别以 、 為圓心,、 為半徑畫弧,即可將圓六等分,)、、、 為四个六等分點(如圖)。
- 以 為圓心,為半徑畫弧 ;以 為圓心,為半徑畫弧 ,兩弧交於 點。
- 以 為圓心,取的长度 為半徑畫弧 ,交圓於 、 兩點。
- 、、、 四點將圓四等分。
證明
設圓的半徑為,容易得出、、、、、、的長度都是,可以得出,根據畢氏定理可以得出,因此、、、四點將圓四等分。
參見
- 拿破崙定理
- 尺規作圖
- 圓規作圖
註解
- Georg Mohr, Euclides Danicus (Amsterdam: Jacob van Velsen, 1672).
- Schogt, J. H. (1938) "Om Georg Mohr's Euclides Danicus," Matematisk Tidsskrift A , pages 34-36.
參考資料
- Napoleon's Problem (页面存档备份,存于)MathWorld
- 拿破崙分圓
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.