大稀有三角六十面體

由於這個立體是完全星形二十面體的對偶多面體，根據對偶多面體的性質，其為面與頂點互換，也就是說，對偶多面體是將原始多面體的頂點變成對偶多面體的面、原始多面體的面變成對偶多面體的頂點，邊與新的頂點連接，因此原有多面體的面會成為對偶多面體的頂點圖，反之亦然，[6]也就是說大稀有三角六十面體的頂點圖會是九角星，對應完全星形二十面體的面。頂點圖為九角星意味著頂點周圍之面的排列方式會依循九角星邊的連接方式：[1]

組成大稀有三角六十面體 頂點周圍面的 排列方式（頂點圖，以藍色表示）

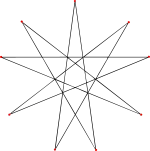大稀有三角六十面體 的頂點圖

大稀有三角六十面體由60個等腰三角形組成，也就是說大稀有三角六十面體的組成面為等腰三角形。這些等腰三角形有著面跟其他的面相交的性質，[4]因此會導致面有部分隱沒在圖形內部，並非所有部分皆可見，因此難以直接從外觀識別出其等腰三角形面。如下圖，露在外面的部份已藍色表示、隱沒於形狀內部的部分以白色表示，黑線為與其他面的交線。

大稀有三角六十面體的頂點座標為：[1]

${\displaystyle \left(\pm {\frac {1}{2}},\,\pm {\frac {1}{2}},\,\pm {\frac {1}{2}}\right)}$、

和${\displaystyle \left(\pm {\frac {\varphi }{2}},\,\pm {\frac {\varphi ^{-1}}{2}},\,0\right)}$的偶排列。

其中${\displaystyle \varphi }$為${\displaystyle {\frac {1+{\sqrt {5}}}{2}}}$，是黃金比例。

大稀有三角六十面體是正十二面體的刻面多面體，即把正十二面體的頂點用其他邊的排列方式重新連接，而不新增頂點或改變頂點的位置。大稀有三角六十面體將正十二面體的頂點改由三個頂點連成三角形。[1][4]

這意味著正十二面體與大稀有三角六十面體共用相同的頂點布局[1]。

小稀有三角六十面體

大稀有三角六十面體的3D模型

作為抽象多面體，大稀有三角六十面體與小稀有三角六十面體（）拓樸同構。[1]小稀有三角六十面體同樣是正十二面體的刻面多面體，但刻面的方式與大稀有三角六十面體不同：構成小稀有三角六十面體的等腰三角形來自於正十二面體頂面的一個頂點和底面的兩個頂點。[9]其對偶多面體是稀有九角星二十面體，即由星形二十面體的D胞所構成的星形多面體。[9]

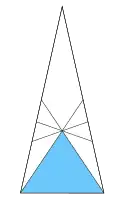小稀有三角六十面體 的面 （藍色為露在立體 外部的部分）	小稀有三角六十面體相對於 正十二面體的刻面[9] 刻面後的面以黃色表示

小稀有三角六十面體外觀與凹五角錐十二面體非常相似。小稀有三角六十面體在外觀上皆為每個面向內凹陷五角錐型的立體，差別僅在凹陷程度不同：小稀有三角六十面體的凹陷程度比凹五角錐十二面體來的淺。

• 
  小稀有三角六十面體
• 
  凹五角錐十二面體

五角柱七百二十胞體
外部圖片 五角柱七百二十胞體的各階級構造
類型	稀有均勻多胞體
維度	4
識別
名稱	五角柱七百二十胞體
鮑爾斯縮寫	paphacki[10]
性質
胞	720個五角柱
面	1800個正方形 720個正五邊形
邊	1200
頂點	120
組成與佈局
顶点图	大稀有三角六十面體
對稱性
對稱群	H4, order 14400
特性
等角、 等胞

大稀有三角六十面體是五角柱七百二十胞體（pentagon-prismatic heptacosicosachoron）的頂點圖。[7][10]五角柱七百二十胞體是邊的領導元素同於小星形一百二十胞体（small stellated 120-cell）的四維稀有均勻多胞體。[10]這種幾何結構非常複雜，堪稱是同類幾何結構中最複雜的例子之一。[7]

五角柱七百二十胞體由720個胞、2520個面、1200條邊和120個頂點所組成。其720個胞皆為五角柱。在其2520個面中，有1800個正方形和720個正五邊形。每個頂點都是60個五角柱的公共頂點，對應的頂點圖為大稀有三角六十面體。[7][10]

五角柱七百二十胞體的頂點座標為：

${\displaystyle \left(\pm 1,\,0,\,0,\,0\right)}$、

${\displaystyle \left(\pm {\frac {1}{2}},\,\pm {\frac {1}{2}},\,\pm {\frac {1}{2}},\,\pm {\frac {1}{2}}\right)}$、

以及${\displaystyle \left(\pm {\frac {1+{\sqrt {5}}}{4}},\,\pm {\frac {{\sqrt {5}}-1}{4}},\,\pm {\frac {1}{2}},\,0\right)}$的全排列。[10]