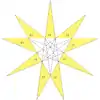
完全星形二十面體

將正二十面體的原有的面延伸成無窮平面，並由其向外延伸的相交點構成的立體稱為正二十面體的星形化體，或簡稱為星形二十面體。書籍《五十九種二十面體》為正二十面體的星形化體提供了一個系統性的規則，並根據其規則給予了一套表示系統，稱為杜瓦表示法。其列舉了正二十面體向外延伸後有可能相交出的面，稱為星形二十面體的胞。杜瓦表示法主要以星形二十面體所佔據的胞來命名。完全星形二十面體正好佔據了最外層「h」層的所有胞，因此完全星形二十面體在杜瓦表示法中可以用H來表示。[9]

完全星形二十面體的多面體模型可以由12個上圖中的面組來構成，每組面折成五個錐體

簡單多面體是指這個多面體中的面不會與同一個多面體的另一個面相交的多面體。若完全星形二十面體要成為一個簡單多面體，則需要在這多面體中相交的面上放置新的頂點和邊，並將原本的九角星面分割成9個三角形面。這樣的多面體共有180個面、[15]270條邊和92個頂點，且歐拉示性數為2。[16]

其92個頂點分別位於3個同心的球面上。最內層有20個頂點，來自一個正十二面體；中間那層有12頂點，來自一個正二十面體；最外層的60個頂點來自一個不均勻的截角二十面體。這三層的半徑比為：[3]

${\displaystyle {\sqrt {{\frac {3}{2}}\left(3+{\sqrt {5}}\right)}}\,:\,{\sqrt {{\frac {1}{2}}\left(25+11{\sqrt {5}}\right)}}\,:\,{\sqrt {{\frac {1}{2}}\left(97+43{\sqrt {5}}\right)}}\,}$

凸包和其他層的頂點

內層	中層	外層	全部
20個頂點	12個頂點	60個頂點	92個頂點
正十二面體	正二十面體	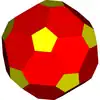不均勻截角二十面體	完全星形二十面體

在上述條件下將完全星形二十面體重建成面不會自我相交的三維立體結構後，其邊長將變為${\displaystyle a}$、${\displaystyle a\varphi }$、${\displaystyle a\varphi ^{2}}$與${\displaystyle a\varphi ^{2}{\sqrt {2}}}$（其中${\displaystyle \varphi }$為黃金比例）。而上述3個分層（內層正十二面體、中層正二十面體、外層不均勻截角二十面體）分別的外接球半徑（內層${\displaystyle R_{12}}$、中層${\displaystyle R_{20}}$、外層${\displaystyle R_{60}}$）為：[3]

${\displaystyle R_{12}={\sqrt {\frac {3\left(3+{\sqrt {5}}\right)}{2}}}\,a}$

${\displaystyle R_{20}={\sqrt {\frac {25+11{\sqrt {5}}}{2}}}\,a}$

${\displaystyle R_{60}={\sqrt {\frac {97+43{\sqrt {5}}}{2}}}\,a}$

其表面積${\displaystyle S}$和體積${\displaystyle V}$為：[3]

${\displaystyle S={\frac {1}{20}}(13211+{\sqrt {174306161}})a^{2}\,}$

${\displaystyle V=(210+90{\sqrt {5}})a^{3}\,}$

當完全星形二十面體作為一個星形多面體時，其是一個面自我相交的非凸多面體，共有20面、90個邊和60個頂點。其每個面都是與施萊夫利符號為 {9/4} 的九角星相近的形狀。[1]

20個與施萊夫利符號為 {9/4} 的九角星形狀相近的面 將其中一個以黃色表示

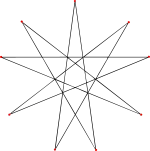完全星形二十面體中九角星面的形狀

完全星形二十面體由20個九角星面組成，[17]由於完全星形二十面體的面有跟其他的面相交的性質，[1]因此，會導致面有部分隱沒在圖形內部，如下圖，露在外面的部份以藍色表示、隱沒於形狀內部的部分以白色表示，黑線為與其他面的交線。

完全星形二十面體可由其九角星面構造，構造方式為以其對應星狀圖的中心胞之正三角形建構一個正二十面體，並透過該正二十面體邊旋轉九角星面構造完全星形二十面體中的一半面數，剩餘部分可透過將前面完成的部分以中心點對稱方式來完成整個完全星形二十面體的構造。[17]