投影 (线性代数)
在线性代数和泛函分析中,投影是从向量空间映射到自身的一种线性变换,满足,也就是说,当两次作用于某个值,与作用一次得到的结果相同(幂等)。是日常生活中“平行投影”概念的形式化和一般化。同现实中阳光将事物投影到地面上一样,投影变换将整个向量空间映射到它的其中一个子空间,并且在这个子空间中是恒等变换[1]。
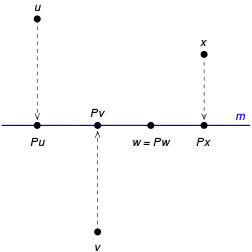
定义
投影的严格定义是:一个从向量空间V射到它自身的线性变换 P 是投影,当且仅当。另外一个定义则较为直观:P 是投影,当且仅当存在V的一个子空间W,使得 P 将所有V中的元素都映射到W中,而且 P 在W上是恒等变换。用数学的语言描述,就是:
- ,使得,并且
简单例子
在现实生活中,阳光在地面上留下各种影子。这就是投影变换最直白的例子。可以理想化地假设阳光都是沿着同一个方向(比如说垂直于地面的角度)照射而来,大地是严格的平面,那么,对于任意一个物体(比如说一只正在飞行的鸟),它的位置可以用向量 (x, y, z) 来表示,而这只鸟在阳光下对应着一个影子,也就是 (x, y, 0)。这样的一个变换就是一个投影变换。它将三维空间中的向量 (x, y, z) 到映射到向量 (x, y, 0) 。这是在 x-y 平面上的投影。这个变换可以用矩阵表示为
因为对任意一个向量 (x, y, z) ,这个矩阵的作用是:
注意到如果一个向量原来就是表示地面上的一点的话(也就是说它的z分量等于0),那么经过变换 P 后不会有改变。也就是说这个变换在子空间 x-y 平面上是恒等变换,这证明了 P 的确是一个投影。
另外,
所以 P = P2,这也证明 P 的确是投影。
基本性质
这里假定投影所在的向量空间W是有限维的(因此不需要考虑如投影的连续性之类的问题)。假设子空间U与V分别为 P 的像空间与零空间(也叫做核)。那么按照定义,有如下的基本性质:
- 按照定义,P是等幂的(即)
- P 在像空间U上是恒等变换:
- 整个向量空间可以分解成子空间U与V的直和:。也就是说,空间里的每一个向量,都可以以唯一的方式写成两个向量与的和:,并且满足, , 其中、。
用抽象代数的术语来说,投影 P 是幂等的线性变换(P2 = P)。因此它的极小多项式是。因式分解后可以看到,这个多项式只有相异的单根(没有多重根),因此 P 是可对角化矩阵。极小多项式也显示出了投影的特性: 像空间与零空间分别是是对应于特征值1和0的特征空间,并给出了整个空间的一个直和分解。
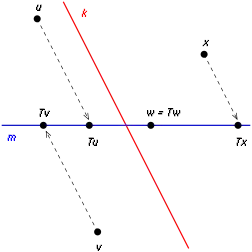
正如日常生活中阳光沿着一定的方向将影子投射到地面上,一般的投影变换也可以称为是沿着W到U上的投影。由于向量空间分解成直和的方式一般不是唯一的(阳光可以顺着不同的方向照射),给定一个子空间 V(地面),一般的说有很多到V 的投影(沿不同的W)。
正交投影
如果向量空间被赋予了内积且是完備的,那么就可以定义正交和其它相关的概念(比如线性算子的自伴随性)了。正交投影是指值域和零空间相互正交的投影,也就是说,對於任意,,它们的内积都等于0。一个投影是正交投影,当且仅当它是自伴算子,以下為證明:如果投影 是自伴算子,那么
- 其中 表示 的伴随算子。
所以 是正交投影。相反的,如果 是正交投影,由於
- 因此我們有
鉴于 是任意選取的,必然有 或 由於一定是自伴算子,因此可知 與 也是自伴算子。
这意味着正交投影的矩阵有特殊的性质。如果投影是在实向量空间中,那么它对应的矩阵是对称矩阵: 。如果投影是在虚向量空间中,那么它的矩阵则是埃尔米特矩阵:
例子
正交投影的最简单的情况是到(过原点)直线上的正交投影。如果 u 是这条直线的单位方向向量,则投影给出为
这个算子保留 u 不变(),并且它作用在所有正交于 u 的向量上都是0(如果,那么 ),证明它的确是到包含 u 的直线上的正交投影[2]。
这个公式可以推广至到在任意维的子空间上的正交投影。设 u1, …, uk 是子空间 U 的一组正交基,并设 A 为一个n×k 的矩阵,它的列向量是 u1, …, uk。那么投影:
也是正交的。矩阵 AT 是在 U 的正交补变为零的偏等距同构,而 A 是把 U 嵌入底层向量空间的等距同构。PA 的值域因此是 A 的“终空间”(final space)。ATA 是在 U 上的恒等算子也是明显的。
正交条件也可以去除。如果 u1, …, uk 是(不必须正交)基,而 A 是有这些向量作为列的矩阵,则投影是
- 。[4]
矩阵 AT 仍把 U 嵌入到低层向量空间中但一般不再是等距的。矩阵 (ATA)−1 是恢复规范的“规范化因子”。例如,秩-1 算子 uuT 不是投影,如果 ||u|| ≠ 1。在除以 uTu = \|u\|2 之后,我们得获得了到 u 所生成的子空间的投影 u(uTu)−1uT。
所有这些公式对于复数内积空间也成立,假如用共轭转置替代转置。
在赋范向量空间上的投影
当底层向量空间 X 是(不必需有限维)赋范向量空间,需要考虑无关于有限维情况的分析问题,假定现在 X 是巴拿赫空间。
上面讨论的多数代数概念转移到这个上下文后幸存下来了。给定的 X 的直和分解成补子空间仍指定一个投影,反之亦然。如果 X 是直和 X = U ⊕ V,则定义自 P(u + v) = u 的算子仍是有值域 U 和核 V 的投影。明显的也 P2 = P。反过来说,如果 P 是在 X 上的投影,就是说 P2 = P,则很容易验证 (I − P)2 = (I − P)。换句话说,(I − P) 也是投影。关系 I = P + (I − P) 蕴涵了 X 是直和 Ran(P) ⊕ Ran(I − P)。
但是相对于有限维情况,投影一般不必须是连续的。如果 X 的子空间 U 在规范拓扑下不闭合,则到 U 上的投影是不连续的。换句话说,连续投影 P 的值域一定是闭合子空间。进一步的,连续投影(事实上,一般的连续线性算子)的核是闭合的。所以连续投影 P 把 X 分解成两个互补的闭合子空间: X = Ran(P) ⊕ Ker(P) = Ran(P) ⊕ Ran(I − P)。
反命题在有额外假定条件下也成立。假设 U 是 X 的闭合子空间。如果存在一个闭合子空间 V 使得 X = U ⊕ V,则有值域 U 和核 V 的投影 P 是连续的。这是从闭合图定理推出的。假定 xn → x 而 Pxn → y。需要证明 Px = y。因为 U 是闭合的且 {Pxn} ⊂ U, y 位于 U 中,就是说 Py = y。还有 xn − Pxn = (I − P)xn → x − y。因为 V 是闭合的且 {(I − P)xn} ⊂ V,我们有了 x − y ∈ V,就是说 P(x − y) = Px − Py = Px − y = 0,这证明了这个断言。
上述论证利用 U 和 V 都是闭合的假定。一般的说,给定一个闭合子空间 U, 不需要存在一个互补的闭合子空间 V,尽管对于希尔伯特空间总是可以采取正交补得到。对于巴拿赫空间,一维子空间总是有闭合的补子空间。这是 哈恩-巴拿赫定理的直接推论。设 U 是 u 的线性扩张。通过哈恩-巴拿赫定理,存在一个有界线性泛函 φ,使得 φ(u) = 1。算子 P(x) = φ(x)u 满足 P2 = P,就是说它是个投影。φ 的有界性蕴涵了 P 的连续性,因此 Ker(P) = Ran(I − P) 是 U 的闭合补子空间。
注解
- Meyer, pp 386+387
- Meyer, p. 431
- Meyer, equation (5.13.4)
- Meyer, equation (5.13.3)
- Meyer, equation (7.10.39)
引用
- N. Dunford and J.T. Schwartz, Linear Operators, Part I: General Theory, Interscience, 1958.
- Carl D. Meyer, Matrix Analysis and Applied Linear Algebra (页面存档备份,存于), Society for Industrial and Applied Mathematics, 2000. ISBN 978-0-89871-454-8.