拋物柱面坐標系
拋物柱面坐標系(英語:)是一種三維正交坐標系。往 z-軸方向延伸二維的拋物線坐標系 ,則可得到拋物柱面坐標系。其坐標曲面是共焦的拋物柱面。拋物柱面坐標可以應用於許多物理問題。例如,物體邊緣的位勢論。
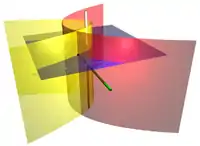
拋物柱面坐標系的幾個坐標曲面。紅色拋物柱面的 。黃色拋物柱面的 。藍色薄面的 。z-軸是垂直的,以白色表示。 x-軸以綠色表示。三個曲面相交於點 P (顯示為黑色的圓球),直角坐標大約為 。

拋物線坐標系的 和 的等值曲線。横軸與縱軸分別為 x-軸與 y-軸。拋物線坐標系可以往 z-軸延伸。對於任意 z-坐標,這曲線圖都正確無誤。
基本定義
直角坐標 可以用拋物柱面坐標 表示為
- 、
- 、
- ;
其中, , 。
- ,
而坐標 為常數的曲線形成共焦的,凹性往 -y-軸的拋物柱面:
- 。
這些拋物柱面的焦線的位置都在 z-軸。
徑向距 的公式為
- 。
當解析經典力學的反平方連心力問題時,假若採用拋物柱面坐標的哈密頓-亞可比方程式,則會用到這很有用的公式。參閱 拉普拉斯-龍格-冷次向量。
標度因子
拋物柱面坐標 與 的標度因子相等;而 的標度因子是 1 :
- 、
- 。
無窮小體積元素是
- 。
- 。
其它微分算子,像 、 ,都可以用 坐標表示,只要將標度因子代入在正交坐標系條目內對應的一般公式。
應用
拋物柱面坐標有一個經典的應用,這是在解析像拉普拉斯方程或亥姆霍茲方程這類的偏微分方程式。在這些方程式裏,拋物柱面坐標允許分離變數法的使用。個典型的例題是,有一塊半無限的平板導體,請問其周圍的電場為什麼?應用拋物柱面坐標,我們可以精緻地分析這例題。
參閱
參考文獻
- Korn GA, Korn TM. . New York: McGraw-Hill. 1961: p. 181. ASIN B0000CKZX7.
- Sauer R, Szabó I. . New York: Springer Verlag. 1967: p. 96.
- Zwillinger D. . Boston, MA: Jones and Bartlett. 1992: p. 114. ISBN 0-86720-293-9. Same as Morse & Feshbach (1953), substituting uk for ξk。
- Moon P, Spencer DE. . corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: pp. 21–24 (Table 1.04). ISBN 978-0387184302.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.