莫爾圓

莫爾圓（Mohr's circle）得名自德國土木工程師克里斯汀·奧圖·莫爾，是一種用二維方式表示柯西应力张量轉換關係的圖。

圖1：三維應力下的莫爾圓

先針對假設為連續的物體進行應力分析，之後特定一點的柯西应力张量分量會和坐標系有關。莫爾圓是用圖形的方法去確認一個旋轉坐標系上的應力分量，也就是在同一點上，但是作用在不同方向平面上的分量。

圓上每一個點的橫坐標 $\sigma _{\mathrm {n} }$ 及縱坐標 $\tau _{\mathrm {n} }$ 都是在這個旋轉坐標系統上某一個方向的正應力及剪應力。換句話說，莫爾圓表示了在所有方向平面上應力狀態的軌跡，而X軸和Y軸為應力元素的主軸。

卡爾·卡爾曼是第一個想到用圖形來表示應力的人，他是在分析水平樑承受彎曲時的縱向應力及垂直應力時所想到的。莫爾的貢獻不止是用莫爾圓表示二維及三維的應力，他也根據莫爾圓發展了結構失效判定的準則[1]。

其他表示應力狀態的方式有拉梅應力橢球及柯西應力二次曲線（Cauchy's stress quadric）。

莫爾圓可以擴展到對稱的 2x2 張量，包括應變及轉動慣量張量。

應力及莫爾圓

圖2：在有受力可變形物體（假設為連續體）中的應力F

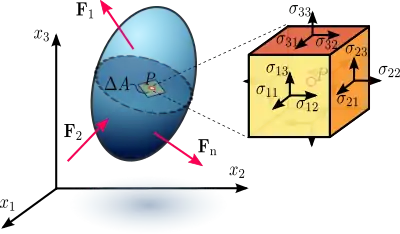
考慮一個會變形的物體（假設為連續體），若受到外力（可能是表面力或是物體力），物體的內部就會有力的分布。物體內部的力會依循歐拉運動定律，正如物體受力依循牛頓運動定律一様。物體內部力的強度可以用應力來表示。因為物體假設為連續體，其內部的力也是會均勻分佈在其體積中。

在工程中（例如結構工程、機械工程或土力工程）會透過應力分析來分析一物體中應力的的分佈，例如隧道中岩石的應力，飛機機翼的應力，或是建築物中樑柱的應力等。計算應力分布也就表示要知道物體中每一點的應力。據奧古斯丁·路易·柯西的理論，（假設為連續體的）物體中任何一點的應力（圖2），可以完全由二階(2,0)型的張量中的九個應力元素 $\sigma _{ij}$ 完全決定，此二階張量稱為柯西应力张量, ${\boldsymbol {\sigma }}$ :

{\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{y}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{z}\\\end{matrix}}\right]

圖3：連續體中的一點在平面應力條件下的應力轉換

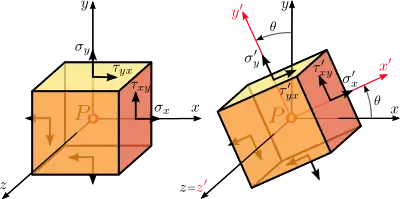
若確定了一物體在特定坐標系統 $(x,y)$ 下的應力分佈，有可能需要知道特定一點 $P$ 相對另一個有旋轉的坐標系統 $(x',y')$ 下的應力張量，也就是在需要關注的點，在特定角度下的的應力張量。而此坐標系統 $(x',y')$ 和原有的坐標系統 $(x,y)$ 之間有一個角度差（圖3）。例如，一般會需要知道最大的正向應力以及最大的剪應力，也需要知道其對應的方向。因此，需要發展一種張量轉換的方式，可以配合坐標系統的旋轉得到新坐標系統的張量。依照張量的定義，柯西应力张量遵守張量轉換定律。應力的莫爾圓是用圖解方式來說明柯西应力张量轉換定律的方式。

二維張量下的莫爾圓

圖4：連續體中的一點在平面應力條件下的應力分量

在二維下，一點 $P$ 相對于垂直方向的應力張量可以用三個應力向量完全表示。在垂直坐標系統 $(x,y)$ 下，其應力分量為：法向應力 $\sigma _{x}$ 及 $\sigma _{y}$ ，以及剪應力 $\tau _{xy}$ 。由於角動量守恆，柯西應力張量會有對稱性，也就是 $\tau _{xy}=\tau _{yx}$ ，因此柯西應力張量可以寫成：

{\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{x}&\tau _{xy}&0\\\tau _{xy}&\sigma _{y}&0\\0&0&0\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{xy}&\sigma _{y}\\\end{matrix}}\right]

其目的是在另一個通過 $P$ 點，但存在角度差的坐標系統 $(x',y')$ 下，找到應力分量 $\sigma _{\mathrm {n} }$ 及 $\tau _{\mathrm {n} }$ （圖4）。坐標系統 $(x',y')$ 和原坐標系統 $(x,y)$ 的角度差即為 $\theta$ 。

莫爾圓的方程

要推導二維平面應力及平面應變的莫爾圓方程，先考慮一個位在位置 $P$ 的二維的無限小方形元素（圖4），和 $y$ - $z$ 平面平行。

利用無限小元素上的力平衡，正向應力 $\sigma _{\mathrm {n} }$ 及剪應力 $\tau _{\mathrm {n} }$ 的大小為：

\sigma _{\mathrm {n} }={\frac {1}{2}}(\sigma _{x}+\sigma _{y})+{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\cos 2\theta +\tau _{xy}\sin 2\theta

\tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta

莫爾圓參數式的推導－利用力平衡

利用

\sigma _{\mathrm {n} }

方向（

x'

軸）的力平衡（圖4），而且假設

\sigma _{\mathrm {n} }

作用的面積為

dA

，可得：

\ {\begin{aligned}\sum F_{x'}&=\sigma _{\mathrm {n} }dA-\sigma _{x}dA\cos ^{2}\theta -\sigma _{y}dA\sin ^{2}\theta -\tau _{xy}dA\cos \theta \sin \theta -\tau _{xy}dA\sin \theta \cos \theta =0\\\sigma _{\mathrm {n} }&=\sigma _{x}\cos ^{2}\theta +\sigma _{y}\sin ^{2}\theta +2\tau _{xy}\sin \theta \cos \theta \\\end{aligned}}

再考慮以下的關係

\cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}},\qquad \sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}\qquad

及

\qquad \sin 2\theta =2\sin \theta \cos \theta

可以得到

\sigma _{\mathrm {n} }={\frac {1}{2}}(\sigma _{x}+\sigma _{y})+{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\cos 2\theta +\tau _{xy}\sin 2\theta

再考慮 $\tau _{\mathrm {n} }$ 方向（ $y'$ 軸）的力平衡（圖4），再假設 $\tau _{\mathrm {n} }$ 作用的面積是 $dA$ ，可得：

\ {\begin{aligned}\sum F_{y'}&=\tau _{\mathrm {n} }dA+\sigma _{x}dA\cos \theta \sin \theta -\sigma _{y}dA\sin \theta \cos \theta -\tau _{xy}dA\cos ^{2}\theta +\tau _{xy}dA\sin ^{2}\theta =0\\\tau _{\mathrm {n} }&=-(\sigma _{x}-\sigma _{y})\sin \theta \cos \theta +\tau _{xy}\left(\cos ^{2}\theta -\sin ^{2}\theta \right)\\\end{aligned}}

再考慮以下的關係

\cos ^{2}\theta -\sin ^{2}\theta =\cos 2\theta \qquad

及

\qquad \sin 2\theta =2\sin \theta \cos \theta

可以得到

\tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta

上述二個方程也可以用柯西應力張量的張量變換定律來求得，這和在 $\sigma _{\mathrm {n} }$ 及 $\tau _{\mathrm {n} }$ 方向用力平衡計算是等效的。

莫爾圓參數式的推導－利用張量變換

應力張量變換定律可以表示為

{\begin{aligned}{\boldsymbol {\sigma }}'&=\mathbf {A} {\boldsymbol {\sigma }}\mathbf {A} ^{T}\\\left[{\begin{matrix}\sigma _{x'}&\tau _{x'y'}\\\tau _{y'x'}&\sigma _{y'}\\\end{matrix}}\right]&=\left[{\begin{matrix}a_{x}&a_{xy}\\a_{yx}&a_{y}\\\end{matrix}}\right]\left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{yx}&\sigma _{y}\\\end{matrix}}\right]\left[{\begin{matrix}a_{x}&a_{yx}\\a_{xy}&a_{y}\\\end{matrix}}\right]\\&=\left[{\begin{matrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \\\end{matrix}}\right]\left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{yx}&\sigma _{y}\\\end{matrix}}\right]\left[{\begin{matrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{matrix}}\right]\end{aligned}}

將等號右側展開，再配合 $\sigma _{x'}=\sigma _{\mathrm {n} }$ 及 $\tau _{x'y'}=\tau _{\mathrm {n} }$ ，可得：

\sigma _{\mathrm {n} }=\sigma _{x}\cos ^{2}\theta +\sigma _{y}\sin ^{2}\theta +2\tau _{xy}\sin \theta \cos \theta

再加上以下的條件

\cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}},\qquad \sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}\qquad

及

\qquad \sin 2\theta =2\sin \theta \cos \theta

可得

\sigma _{\mathrm {n} }={\frac {1}{2}}(\sigma _{x}+\sigma _{y})+{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\cos 2\theta +\tau _{xy}\sin 2\theta

$\tau _{\mathrm {n} }=-(\sigma _{x}-\sigma _{y})\sin \theta \cos \theta +\tau _{xy}\left(\cos ^{2}\theta -\sin ^{2}\theta \right)$

再加上以下的條件

\cos ^{2}\theta -\sin ^{2}\theta =\cos 2\theta \qquad

及

\qquad \sin 2\theta =2\sin \theta \cos \theta

可得

\tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta

此時不需要計算 $\sigma _{x'}$ 垂直的應力成份 $\sigma _{y'}$ ，因為在推導莫爾圓時還不需要此成份

這二個方程是莫爾圓的參數式。在方程中， $2\theta$ 為參數，而 $\sigma _{\mathrm {n} }$ 和 $\tau _{\mathrm {n} }$ 為坐標，因此表示若選擇適當的坐標系統，使 $\sigma _{\mathrm {n} }$ 為橫軸， $\tau _{\mathrm {n} }$ 縱軸，給定參數 $\theta$ ，會給定在莫爾圓上的一點。

若從參數式中消去參數 $2\theta$ ，可以得到非參數式的莫爾圓方程。可以用重組 $\sigma _{\mathrm {n} }$ 及 $\tau _{\mathrm {n} }$ 的方程來達到。先將第一式等號右側的第一項移到等號左邊，二式平方後相加，可得

{\begin{aligned}\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\right]^{2}+\tau _{\mathrm {n} }^{2}&=\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}\\(\sigma _{\mathrm {n} }-\sigma _{\mathrm {avg} })^{2}+\tau _{\mathrm {n} }^{2}&=R^{2}\end{aligned}}

其中

R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}\quad {\text{and}}\quad \sigma _{\mathrm {avg} }={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})

這就是圓（莫爾圓）的方程

(x-a)^{2}+(y-b)^{2}=r^{2}

在 $(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$ 坐標系統中，其半徑 $r=R$ ，圓心在坐標 $(a,b)=(\sigma _{\mathrm {avg} },0)$ 處。

符號體系

在使用莫爾圓時，需考慮兩組分別的符號體系，一個是針對實體空間下應力分量的符號體系，另一個是針對「莫爾圓空間」下應力分量的符號體系。此外，工程力學（結構工程及機械工程）文獻用的體系和地質力學用的符號體系不同。沒有所有系統都適用的標準符號體系，是否要使用特定的符號體系取決於計算及詮釋特定問題的方便程度。

上述圖4的莫爾圓推導都是使用工程力學的符號體系，以下也會繼續使用工程力學的符號體系。

實體空間符號體系

為了描述柯西應力張量的方便（圖3及圖4），應力分量的第一個下標表示應力分量作用的面，第二個下標表示應力分量的方向。因此 $\tau _{xy}$ 是作用在以 $x$ 軸正向為其法向量的平面上，而方向是往 $y$ 軸的正方向。

在實體空間符號體系，正的正向應力是由作用平面往外（張力），負的正向應力是由作用平面往內（壓縮力）（圖5）。

在實體空間符號體系中，正剪應力在法向量為正的材料元素平面上，其作用方向會往軸的正方向，同樣的，正剪力在法向量為負的材料元素平面上，其作用方向會往軸的負方向。例如作用在正向平面的剪應力 $\tau _{xy}$ 和 $\tau _{yx}$ 為正，因為這二個剪應力的作用方向往 $y$ 軸及 $x$ 軸的正方向（圖3）。而相對應的作用在負向平面的剪應力 $\tau _{xy}$ 和 $\tau _{yx}$ ，其作用方向往 $y$ 軸及 $x$ 軸的負方向，因此這二個剪應力也為正。

莫爾圓空間符號體系

圖5 繪制莫爾圓時，工程力學符號體系下的應力。此條目會依照圖中的符號體系 # 3

在莫爾圓空間符號體系中，應力的符號體系和實體空間符號體系中的相同：正的正向應力是由作用平面往外（張力），負的正向應力是由作用平面往內（壓縮力）

不過剪應力的符號體系和實體空間符號體系中的不同。在莫爾圓空間符號體系中，正的剪應力會使材料往逆時針方向旋轉，而負的剪應力會使材料往順時針方向旋轉。因此在莫爾圓空間中，剪應力分量 $\tau _{xy}$ 為正，而 $\tau _{yx}$ 為負。這和實體空間符號體系中 $\tau _{xy}$ 和 $\tau _{yx}$ 符號相同的情形不同。

在繪製莫爾圓時，有二個作法可以繪製在數學上正確的莫爾圓：

將正的剪應力畫在上方（圖5，符號體系#1）
將正的剪應力畫在下方，也就是 $\tau _{\mathrm {n} }$ 軸倒置（圖5，符號體系#2）

將正的剪應力畫在上方會讓莫爾圓上的 $2\theta$ 角為正值時，旋轉方向是順時針旋轉，這和實體空間符號體系中的相反。因此有些作者[2]會選擇讓正的剪應力畫在下方，這會讓莫爾圓上的 $2\theta$ 角為正值時，旋轉方向是逆時針旋轉，類似實體空間符號體系的情形。

為了克服剪應力軸往下才是正向的問題，有另外一種「替代的」符號體系，其中正的剪應力假設為將材料將順時針方向旋轉，而負的剪應力假設為將材料將逆時針方向旋轉（圖5，符號體系#3）。在「替代」體系下，正的剪應力軸往上，而且在莫爾圓上 $2\theta$ 為正值時，旋轉方向為逆時針。此符號體系產生的莫爾圓和圖5，符號體系#2中的相同，因為正的剪應力 $\tau _{\mathrm {n} }$ 也是會逆時針旋轉的剪應力，也畫在下方。而負的剪應力 $\tau _{\mathrm {n} }$ 也是會順時針旋轉的剪應力，也畫在上方。

此條目在實體空間符號體系中，會依照工程力學的符號體系，而在莫爾圓空間中，會使用「替代的」符號體系（圖5，符號體系#3）。

繪製莫爾圓

圖6：在平面應力及平面應變的條件下繪製莫爾圓（二倍角的作法）
在應力分析後，可以找到材料中一點

P

上的應力分量

\sigma _{x}

、

\sigma _{y}

及

\tau _{xy}

。應力分量作用在二個互相垂直的

A

平面及

B

平面，兩者都通過

P

點。莫爾圓上

A

點和

B

點的坐標是在

A

平面及

B

平面上的應力分量。因此可以用莫爾圓找到應力分量

\sigma _{\mathrm {n} }

及

\tau _{\mathrm {n} }

，也就是在同一點上，但作用在其他平面

D

上的應力分量。

{\overline {OB}}

線和

{\overline {OD}}

線之間的夾角是通過

P

點的平面

B

和平面

D

的法向量的夾角

假設已知待研究物體上的點 $P$ 的應力分量 $\sigma _{x}$ 、 $\sigma _{y}$ 及 $\tau _{xy}$ ，如圖4所示。以下方法可以繪製點 $P$ 的莫爾圓，以表示其應力狀態。

繪制笛卡爾坐標系統 $(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$ ，橫軸為 $\sigma _{\mathrm {n} }$ ，縱軸為 $\tau _{\mathrm {n} }$ 。
在 $(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$ 空間中，畫出二點 $A(\sigma _{y},\tau _{xy})$ 及 $B(\sigma _{x},-\tau _{xy})$ ，分別是作用在二垂直平面 $A$ 平面和 $B$ 平面上的應力分量（圖4及圖6），需依照選擇的符號體系。
用線段 ${\overline {AB}}$ 連接 $A$ 點和 $B$ 點，此即為圓的直徑。
繪製莫爾圓，其圓心 $O$ 是線段 ${\overline {AB}}$ 的中點，也就是此線和 $\sigma _{\mathrm {n} }$ 軸的交點。

找主要正向應力

主要應力的大小是點 $C$ 和點 $E$ （圖6中圓和 $\sigma _{\mathrm {n} }$ 軸的交點）中的橫坐標。最大正向應力 $\sigma _{1}$ 的大小恆為這二個橫坐標中最大的那一個，而 $\sigma _{2}$ 最小正向應力的大小恆為這二個橫坐標中最小的那一個。這二個點的縱坐標為0，對應在主要平面上的剪應力為零，主要應力的大小也可以表示為

\sigma _{1}=\sigma _{\max }=\sigma _{\text{avg}}+R

\sigma _{2}=\sigma _{\min }=\sigma _{\text{avg}}-R

其中平均正向應力 $\sigma _{\text{avg}}$ 的大小是圓心 $O$ 的橫坐標，為

\sigma _{\text{avg}}={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})

其半徑的長度 $R$ 為

R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}

找最大和最小剪應力

最大剪應力和最小剪應力對應圓上最大及最小的縱坐標。這二個點是圓和通過圓心 $O$ 的垂直線的交點。因此，最大和最小剪應力的大小為圓的半徑 $R$

\tau _{\max ,\min }=\pm R

找任意平面的應力分量

如前面所述，在二維應力分析後，可以知道在材料某一點 $P$ 上的應力分量 $\sigma _{x}$ 、 $\sigma _{y}$ 及 $\tau _{xy}$ 。這些應力分量作用在通過 $P$ 點的二垂直平面 $A$ 及 $B$ ，如圖5及圖6所述。莫爾圓也可以計算在莫爾圓上 $D$ 的應力分量 $\sigma _{\mathrm {n} }$ 及 $\tau _{\mathrm {n} }$ ，事實是作用在 $D$ 平面上，此平面也通過 $P$ 點，和 $B$ 平面有夾角 $\theta$ ，計算應力分量有二種方式：倍角法以及平面原點法（origin of planes）

倍角法

如圖6所示，若平面 $D$ 是平面 $B$ 再逆時針旋轉角度 $\theta$ 後的平面，要找到在平面 $D$ 上的應力分量 $(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$ ，可以在莫爾圓上從已知應力點 $B(\sigma _{x},-\tau _{xy})$ 同樣以逆時針旋轉，但旋轉角度 $2\theta$ ，旋轉到點 $D(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$ ，也就是讓 ${\overline {OB}}$ 線和 ${\overline {OD}}$ 線之間的夾角是 $2\theta$ 。

倍角法的作法源自於通過 $P$ 點的二實際平面之間的夾角 $\theta$ （圖4），是其對應應力點 $(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$ 在莫爾圓上和圓心連線形成夾角的一半。

倍角關係是因為莫爾圓的參數式是 $2\theta$ 的函數。也可以從在材料點 $P$ 上的平面 $A$ 和 $B$ 夾角是90度，而在莫爾圓上其應力點夾角為180度看出（90度的兩倍）。

極點法（或平面原點法）

圖7：平面應力及應變的莫爾圓（極點法）。從極點畫的任何直線都會和莫爾圓相交，交點表示在和直線相同角度平面上的應力狀態

第二種方式和要找到莫爾圓上的一個點，稱為極點（pole）或是平面原點（origin of planes）。從極點畫的任何直線都會和莫爾圓相交，交點表示在和直線相同角度的平面上的應力狀態。因此若知道任何特定平面上的應力分量 $\sigma$ 及 $\tau$ ，可以畫一條線通過莫爾圓上的 $\sigma _{\mathrm {n} }$ 和 $\tau _{\mathrm {n} }$ ，且和平面平行，找到莫爾圓上這些線的交點，即為極點。例如，假設有應力狀態如圓7所示，其分量是 $\sigma _{x},\!$ , $\sigma _{y},\!$ 及 $\tau _{xy},\!$ 。首先先從 $B$ 點畫一條線，平行 $\sigma _{x}$ 的作用平面，或是從 $A$ 點畫一條線，平行 $\sigma _{y}$ 的作用平面，任一條線都會和莫爾圓交會，交會的點即為極點。在找到極點後，若要找到和垂直有 $\theta$ 夾角的平面上的應力，可以從極點畫一條平行該平面的線（見圖7）。可以根據直線和莫爾圓的交點找到平面上的正向應力以及剪應力。

找主要平面的方向

最大主要應力及最小主要應力所在的平面方向也稱為主要平面（principal planes），可以用莫爾圓中的∠BOC及∠BOE判斷，然後將二個角度都取一半。因此 ${\overline {OB}}$ 和 ${\overline {OC}}$ 之間的夾角是角∠BOC，是 $\theta _{p}$ （主要平面和平面 $B$ 夾角）角度的二倍。

而 $\theta _{p1}$ 和 $\theta _{p2}$ 也可以用以下的方程取得

\tan 2\theta _{\mathrm {p} }={\frac {2\tau _{xy}}{\sigma _{x}-\sigma _{y}}}

此方程的解會是二個角度，彼此相差 $90^{\circ }$ 。可以直接用圓的幾何求解此方程，或是用圓的參數式，並且讓 $\tau _{\mathrm {n} }$ 等於零（主要平面上的剪應力為0）。

一般三維應力下的莫爾圓

圖10 三維應力下的莫爾圖

若要繪製三維應力下的莫爾圖，需要先量測其主應力的大小 $\left(\sigma _{1},\sigma _{2},\sigma _{3}\right)$ 以及方向 $\left(n_{1},n_{2},n_{3}\right)$ 。

考慮以主應力軸為坐標系統，而不是用 $x_{1}$ , $x_{2}$ , $x_{3}$ 坐標系統，並且假設 $\sigma _{1}>\sigma _{2}>\sigma _{3}$ ，則在一法向量為 $\mathbf {n}$ 的平面，其應力向量 $\mathbf {T} ^{(\mathbf {n} )}$ 的應力分量及剪力分量會滿足下式

{\begin{aligned}\left(T^{(n)}\right)^{2}&=\sigma _{ij}\sigma _{ik}n_{j}n_{k}\\\sigma _{\mathrm {n} }^{2}+\tau _{\mathrm {n} }^{2}&=\sigma _{1}^{2}n_{1}^{2}+\sigma _{2}^{2}n_{2}^{2}+\sigma _{3}^{2}n_{3}^{2}\end{aligned}}

\sigma _{\mathrm {n} }=\sigma _{1}n_{1}^{2}+\sigma _{2}n_{2}^{2}+\sigma _{3}n_{3}^{2}.

由於 $n_{i}n_{i}=n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1$ ，可以用高斯消去法求解 $n_{1}^{2}$ , $n_{2}^{2}$ , $n_{3}^{2}$ ：

{\begin{aligned}n_{1}^{2}&={\frac {\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{2})(\sigma _{\mathrm {n} }-\sigma _{3})}{(\sigma _{1}-\sigma _{2})(\sigma _{1}-\sigma _{3})}}\geq 0\\n_{2}^{2}&={\frac {\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{3})(\sigma _{\mathrm {n} }-\sigma _{1})}{(\sigma _{2}-\sigma _{3})(\sigma _{2}-\sigma _{1})}}\geq 0\\n_{3}^{2}&={\frac {\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{1})(\sigma _{\mathrm {n} }-\sigma _{2})}{(\sigma _{3}-\sigma _{1})(\sigma _{3}-\sigma _{2})}}\geq 0.\end{aligned}}

因為 $\sigma _{1}>\sigma _{2}>\sigma _{3}$ 及 $(n_{i})^{2}$ 都不是負值，因此其分子滿足

\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{2})(\sigma _{\mathrm {n} }-\sigma _{3})\geq 0

因為其分母

\sigma _{1}-\sigma _{2}>0

而且

\sigma _{1}-\sigma _{3}>0

\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{3})(\sigma _{\mathrm {n} }-\sigma _{1})\leq 0

因為其分母

\sigma _{2}-\sigma _{3}>0

而且

\sigma _{2}-\sigma _{1}<0

\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{1})(\sigma _{\mathrm {n} }-\sigma _{2})\geq 0

因為其分母

\sigma _{3}-\sigma _{1}<0

而且

\sigma _{3}-\sigma _{2}<0.

方程式可以寫成

{\begin{aligned}\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})\right)^{2}\\\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3})\right]^{2}\leq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})\right)^{2}\\\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})\right)^{2}\\\end{aligned}}

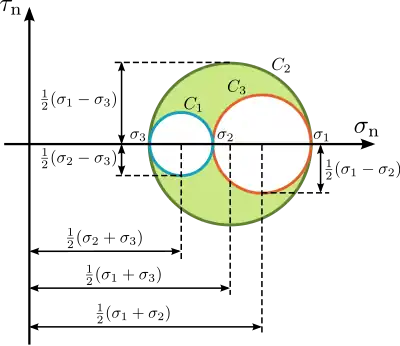
是三個應力莫爾圓 $C_{1}$ , $C_{2}$ 和 $C_{3}$ 的方程，其半徑分別是 $R_{1}={\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})$ , $R_{2}={\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})$ 及 $R_{3}={\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})$ ，而其圓心分別在 $\left[{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3}),0\right]$ , $\left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3}),0\right]$ , $\left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2}),0\right]$ 。

有了上述三個應力莫爾圓的方程，所有可能的應力點 $(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$ 都會在三個應力莫爾圓之間的陰影區域（見圖10）。應力點 $(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$ 可能滿足圓 $C_{1}$ 的方程，或是在圓 $C_{1}$ 的外面，可能滿足圓 $C_{2}$ 的方程，或是在圓 $C_{2}$ 的裡面，可能滿足圓 $C_{3}$ 的方程，或是在圓 $C_{3}$ 的外面。

腳註

Parry, Richard Hawley Grey. 2. Taylor & Francis. 2004: 1–30 [2018-02-05]. ISBN 0-415-27297-1. （原始内容存档于2020-08-07）.
Russell C. Hibbeler. . 2010: 461–462. ISBN 978-0136022305 （英语）.

參考資料

Beer, Ferdinand Pierre; Elwood Russell Johnston; John T. DeWolf. . McGraw-Hill Professional. 1992. ISBN 0-07-112939-1.
Brady, B.H.G.; E.T. Brown. Third. Kluwer Academic Publisher. 1993: 17–29 [2018-02-05]. ISBN 0-412-47550-2. （原始内容存档于2020-08-07）.
Davis, R. O.; Selvadurai. A. P. S. . Cambridge University Press. 1996: 16–26 [2018-02-05]. ISBN 0-521-49827-9. （原始内容存档于2020-08-07）.
Holtz, Robert D.; Kovacs, William D. . Prentice-Hall civil engineering and engineering mechanics series. Prentice-Hall. 1981 [2018-02-05]. ISBN 0-13-484394-0. （原始内容存档于2019-06-08）.
Jaeger, John Conrad; Cook, N.G.W; Zimmerman, R.W. Fourth. Wiley-Blackwell. 2007: 9–41 [2018-02-05]. ISBN 0-632-05759-9. （原始内容存档于2019-06-02）.
Jumikis, Alfreds R. . Van Nostrand Reinhold Co. 1969 [2018-02-05]. ISBN 0-442-04199-3. （原始内容存档于2019-06-08）.
Parry, Richard Hawley Grey. 2. Taylor & Francis. 2004: 1–30 [2018-02-05]. ISBN 0-415-27297-1. （原始内容存档于2020-08-07）.
Timoshenko, Stephen P.; James Norman Goodier. Third. McGraw-Hill International Editions. 1970. ISBN 0-07-085805-5.
Timoshenko, Stephen P. . Dover Books on Physics. Dover Publications. 1983. ISBN 0-486-61187-6.

外部連結

Mohr's Circle and more circles by Rebecca Brannon （页面存档备份，存于）
DoITPoMS Teaching and Learning Package- "Stress Analysis and Mohr's Circle" （页面存档备份，存于）

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Parry-1] Parry, Richard Hawley Grey. 2. Taylor & Francis. 2004: 1–30 [2018-02-05]. ISBN 0-415-27297-1. （原始内容存档于2020-08-07）.

[2] Russell C. Hibbeler. . 2010: 461–462. ISBN 978-0136022305 （英语）.

莫爾圓

應力及莫爾圓

二維張量下的莫爾圓

莫爾圓的方程

符號體系

實體空間符號體系

莫爾圓空間符號體系

繪製莫爾圓

找主要正向應力

找最大和最小剪應力

找任意平面的應力分量

倍角法

極點法（或平面原點法）

找主要平面的方向

一般三維應力下的莫爾圓

相關條目

腳註

參考資料

外部連結