核磁共振波谱法

核磁共振波谱法（英語：，简称 NMR spectroscopy 或 NMR ），又称核磁共振波谱，是将核磁共振现象应用于测定分子结构的一种谱学技术。目前，核磁共振波谱的研究主要集中在1H（氢谱）和13C（碳谱）两类原子核的波谱。

伯明翰 HWB-NMR 中心的 900MHz 核磁谱仪

人们可以从核磁共振波谱上获取很多信息，正如同红外光谱一样，核磁共振波谱也可以提供分子中化学官能团的数目和种类，但除此之外，它还可以提供许多红外光谱无法提供的信息。核磁共振波谱对自然科学研究有着深远的影响，人们不仅可以借助它来研究反应机理，还可以用来研究蛋白质和核酸的结构与功能。供研究的核磁样品可为液体或固体。

波谱这一译名是科学家丁渝提出的[1]。

历史

哈佛大学的珀塞尔小组和斯坦福大学的布洛赫小组在1940年代末和50年代初独立开发了核磁共振波谱法。因为他们的发现，爱德华·珀塞尔（Edward Mills Purcell）和费利克斯·布洛赫（Felix Bloch）分享了1952年度的诺贝尔物理学奖[2]。

基本的NMR技术
NMR样品在薄壁玻璃管中制备 - 一个NMR管。

共振频率

当放置在磁场中时，核磁共振活性的原子核（比如1H和13C），以同位素的频率特性吸收电磁辐射[3]。共振频率，原子核吸收的能量以及信号强度与磁场强度成正比。比方说，在场强为21特斯拉的磁场中，质子的共振频率为900MHz。尽管其他磁性核在此场强下拥有不同的共振频率，但人们通常把21特斯拉和900MHz频率进行直接对应。

样品处理

核磁共振波谱仪通常由一个旋转的样品架，一个非常强的磁铁，一个射频发射器和一个接收器组成，探头（天线组件）在磁铁内部环绕样品，可选择用于扩散测量的梯度线圈和电子设备来控制系统。旋转样品是平均扩散运动所必需的。而扩散常数（扩散有序光谱法或DOSY）[4][5]的测量是在样品静止和离心的情况下进行的，流动池可用于在线分析工艺流程。

氘代NMR溶剂

NMR溶液中的绝大多数原子核属于溶剂，大多数常规溶剂是烃，并含有NMR响应的质子。 因此，氘（氢-2）被取代（99+％）。虽然氘氧化物 (D2O)和氘代DMSO(DMSO-d6)用于亲水分析物，氘代苯也是常见的，但氘代溶剂最常用的是氘代氯仿(CDCl3)。 取决于电子溶剂化效应，不同溶剂中的化学位移稍有不同。NMR波谱通常相对于已知的溶剂残余质子峰值，而不是添加的四甲基硅烷进行校准。

化学位移
化学位移的实例：六硼烷B6H10的NMR谱图显示出频率偏移的峰，这提供了分子结构的线索。（点击阅读解读细节）
条目：化学位移

在一个分子中，各个质子的化学环境有所不同，或多或少的受到周边原子或原子团的屏蔽效应的影响，因此它们的共振频率也不同，从而导致在核磁共振波谱上，各个质子的吸收峰出现在不同的位置上。但这种差异并不大，难以精确测量其绝对值，因此人们将化学位移设成一个无量纲的相对值，即：某一物质吸收峰的频率与标准质子吸收峰频率之间的差异称为该物质的化学位移，常用符号 "δ" 表示，单位为 ppm[6]。而在实际应用中，四甲基硅烷常被作为参照物，计算方法如下：

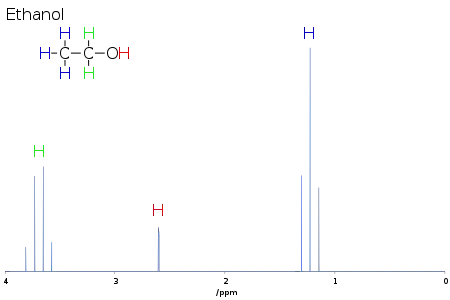
透过不同质子的化学位移，人们可以得出这些质子所处的化学环境，从而得出该分子的结构信息，这种过程称之为“解谱”。比如对于乙醇分子，具有三种不同化学环境的质子，即：甲基、亚甲基和羟基。在其1H谱图上，可以看到3个特有的峰信号各自处于特定的化学位移，其中位于1 ppm的峰信号对应甲基，位于4 ppm的信号对应亚甲基，位于2~3 ppm之间的信号对应羟基，其具体化学位移值和采用的NMR溶剂有关。另外，从峰信号的强度可以得出相对应的质子数量，比如乙醇分子中的甲基拥有3个质子，亚甲基拥有2个质子，在谱图上，对应的甲基和亚甲基峰强度比为3：2。

现代的分析软件可以协助人们通过分析峰信号，从而得出究竟有几个质子形成了此信号。这种方法称作“积分”，即通过计算面积（不单单是高度，还有峰宽度）来得出相关质子数目。但必须指出的是，这种计算方法仅适用于最简单的一维谱，对于更复杂的谱图，比如13C谱，其积分还与原子核的弛豫速率和偶极耦合常数相关，而这些常常被人误解。因此，用积分法来解析复杂核磁谱图是相当困难的。

J-耦合
峰的裂分强度比
单重1
双重1:1
三重1:2:1
四重1:3:3:1
五重1:4:6:4:1
六重1:5:10:10:5:1
七重1:6:15:20:15:6:1
作为信号强度相对于化学位移绘制的乙醇的1H NMR波谱（1维）的例子。 NMR中有三种不同类型的乙醇中的H原子。 -OH基团上的氢（H）不与其他H原子偶合并表现为单峰，但CH3-和-CH2-氢彼此被偶合，分别形成三重态和四重态。

在一维谱图上，除峰信号数量，峰信号强度之外，还有一个有助于解析分子结构的信息，即磁性原子核之间的J-耦合。这种耦合来源于临近磁性原子核的不同自旋状态数的相互作用，这种相互作用会改变原子核自旋在外磁场中进动的能级分布状况，造成能级的裂分，进而造成NMR谱图中的信号峰形状发生劈裂，信号峰的劈裂状态可以得出分子内各原子和官能团之间的连接方式，以及临近的磁性核数目。

两个相邻的氢核之间的耦合遵循一定的规则，n个氢核将把相邻磁性核信号峰劈裂成n+1个多重峰，并且这n+1个多重峰之间的强度关系依照巴斯卡三角形规则。例如，乙醇分子中的甲基峰与相邻的亚甲基耦合，呈三重峰状，三重峰之间的强度比为1：2：1。不过如果一个氢核同时与两个不同性质的氢核进行耦合，则不会得到三重峰，而是得到双双重峰（dd）。要注意的是，如果两个磁性核之间相隔3个化学键以上，耦合就变得十分微弱，以至于不会出现峰的劈裂，但在芳烃和脂环类化合物中三键距离以上的长程耦合通常可以得到较复杂的劈裂峰。

19F与31P通常由于其拥有更大的自旋量子数而显得不同，其余类似，比如氢核与氘核（2D）之间的耦合将把信号峰劈裂为1：1：1。

二级耦合

上文提到的内容是在耦合常数和化学位移间隔相比很小的情况下描述的，如果耦合常数较高，或化学位移间隔小，那么多重峰的情况将变得复杂，特别是两个以上的磁性核进行耦合时，这可以通过增强多重峰当中的特定几个峰，并以牺牲其他峰的代价进行解决，不过在高场谱（比如高频谱）当中，这种现象并不明显，因此提高核磁仪器的频率可以避免此问题。

其中一些模式可以用約翰·波普(John Pople)发表的方法进行分析[7] ，尽管它的范围有限。

随着多重谱之间的频率差增加，二阶效应减小，使得高场谱（即高频谱）NMR频谱比较低频谱显示更小的失真。在早期的60 MHz频谱比通常在200 MHz或更高频率下工作的后期机器的频谱更容易失真。

磁不等价

在芳烃化合物和非弹性分子（比如烯烃）中，常会遇到由于各质子的磁不等价性而带来谱图复杂性增加，这需要计算化模型来辅助分析。

相关谱
条目：关联性磁振频谱

相关谱（Correlation Spectroscopy）是二维核磁波谱的一种，常常简写为COSY。其它二维谱还包括J频谱（J-spectroscopy），交换频谱（EXSY，Exchange spectroscopy），核欧佛豪瑟效应频谱（NOESY，Nuclear Overhauser effect spectroscopy），全相关谱（TOCSY，total correlation spectroscopy），近程碳氢相关（HSQC，Heteronuclear single quantum coherence），远程碳氢相关（HMBC，Heteronuclear multiple bond coherence）等。二维谱在解析分子结构方面可比一维谱提供更多的信息，特别是用一维谱解析复杂分子结构遇到困难的时候，二维谱可以提供帮助。历史上首次二维谱实验方法由比利时布鲁塞尔自由大学（Université Libre de Bruxelles）教授让·吉纳（Jean Jeener）于1971年提出，之后其实验操作由沃尔特·欧（Walter P. Aue），恩里克·巴尔托尔蒂（Enrico Bartholdi）和理查德·恩斯特（Richard R. Ernst）完成，并于1976年发表[8]。

固態核磁共振光譜

液体核磁样品如果放在某些特定的物理环境下，是无法进行研究的，而其它原子级别的光谱技术对此也无能为力。但在固体中，像晶体，微晶粉末，胶质这样的，偶极耦合和化学位移的磁各向异性将在核自旋系统占据主导，在这种情况下如果使用传统的液态核磁技术，谱图上的峰将大大增宽，不利于研究。

目前已经有一系列的高分辨率固体核磁技术被研发出来。高解析固体核磁技术包含两个重要概念，即通过高速旋转来限制分子自取向和消除磁各向异性，对于后者，最常用的旋转方式是魔角旋转（Magic angle spinning），即旋转轴和主磁场的夹角为54.7°。

固体核磁技术常被用于膜蛋白，蛋白纤维和聚合物的结构探究，以及无机化学中的化学分析。但同样可被应用于研究于树叶和燃油。

生物分子核磁共振光谱

蛋白质

利用核磁谱研究蛋白质，已经成为结构生物学领域的一项重要技术手段。X射线单晶衍射和核磁都可获得高分辨率的蛋白质三维结构，不过核磁常局限于35kDa以下的小分子蛋白，尽管随着技术的进步，稍大的蛋白质结构也可以被核磁解析出来。另外，获得本质上非结构化（Intrinsically Unstructured）的蛋白质的高分辨率信息，通常只有核磁能够做到。

蛋白质分子量大，结构复杂，一维核磁谱常显得重叠拥挤而无法进行解析，使用二维，三维甚至四维核磁谱，并采用13C和15N标记可以简化解析过程。另外，NOESY是最重要的蛋白质结构解析方法之一，人们通过NOESY获得蛋白质分子内官能团间距，之后通过电脑模拟得到分子的三维结构。

核酸

“核酸核磁共振”是利用核磁共振光谱学获得关于多核酸如DNA或RNA的结构和动力学的信息。截至2003年，所有已知RNA结构中近一半已通过核磁共振波谱法确定[9] 。

核酸和蛋白质核磁共振波谱相似但存在差异。核酸具有较小的氢原子百分比，这是在NMR光谱学中通常观察到的原子，并且因为核酸双股螺旋是刚性的且大致线性的，所以它们不会自行折叠以产生“长程”相关性[10]。通常用核酸完成的NMR的类型是1H或质子NMR，13C NMR，15N NMR和31P NMR。 几乎总是使用二维核磁共振波谱方法，例如相关光谱学（COSY）和总相干转移光谱学（TOCSY）来检测穿透式核耦合，核欧佛豪瑟效应(Nuclear Overhauser effect)光谱法（NOESY）来检测彼此在空间上靠近的核之间的耦合[11]。

糖类

糖类核磁共振光谱解决糖类结构和构象的问题。

另见

参考来源
  1. 王义遒. . 物理. 2015-03-16, 44 (4): 247 [2015-05-26]. doi:10.7693/wl20150406. （原始内容存档于2015-05-26）.
  2. . Mark Wainwright Analytical Centre - University of Southern Wales Sydney. 9 December 2011 [9 February 2014]. （原始内容存档于27 January 2014）.
  3. Shah, N; Sattar, A; Benanti, M; Hollander, S; Cheuck, L. . The Journal of the American Osteopathic Association. January 2006, 106 (1): 23–27. PMID 16428685. （原始内容存档于2013-04-07）.
  4. Johnson Jr., C. S. . Progress in Nuclear Magnetic Resonance Spectroscopy. 1999, 34: 203–256. doi:10.1016/S0079-6565(99)00003-5.
  5. Neufeld, R.; Stalke, D. . Chem. Sci. 2015, 6: 3354–3364. doi:10.1039/C5SC00670H. 开放获取
  6. 詹姆斯·奇勒. (剑桥大学重印). 理解核磁共振波谱. 尔湾加州大学. [2007-05-11]. （原始内容存档 (PDF)于2020-01-09）.
  7. Pople, J.A.; Bernstein, H. J.; Schneider, W. G. . Can J. Chem. 1957, 35: 65–81.
  8. Martin，G.E; Zekter，A.S.， Two-Dimensional NMR Methods for Establishing Molecular Connectivity; VCH Publishers，Inc: New York，1988 (p.59)
  9. Fürtig, Boris; Richter, Christian; Wöhnert, Jens; Schwalbe, Harald. . ChemBioChem. 2003, 4 (10): 936–62. PMID 14523911. doi:10.1002/cbic.200300700.
  10. Addess, Kenneth J.; Feigon, Juli. . Hecht, Sidney M. (编). . New York: Oxford University Press. 1996. ISBN 0-19-508467-5.
  11. Wemmer, David. . Bloomfield, Victor A.; Crothers, Donald M.; Tinoco, Ignacio (编). . Sausalito, California: University Science Books. 2000. ISBN 0-935702-49-0.

外部链接
维基共享资源上的相关多媒体资源：核磁共振波谱法

核磁技术资讯网站

核磁处理、分析和模拟资源
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.