根系 (数学)

在同構的意義下，秩一的根系僅有一種，由兩個非零向量 ${\displaystyle \{\alpha ,-\alpha \}}$ 組成。此根系記作 ${\displaystyle A_{1}}$。

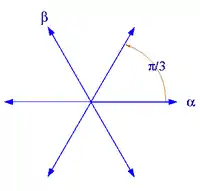
秩二的根系有四種可能，对应于${\displaystyle \sigma _{\alpha }(\beta )=\beta +n\alpha }$，其中${\displaystyle n=0,1,2,3}$的情况[1]。注意根系并不由它生成的格所决定：${\displaystyle A_{1}\times A_{1}}$ 和${\displaystyle B_{2}}$均生成正方形格，而 ${\displaystyle A_{2}}$和${\displaystyle G_{2}}$ 生成六边形格。这仅仅是五种可能的二维格中的两种。 圖解如下：

秩二之根系

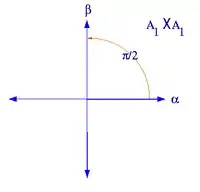根系 A1×A1	根系 A2
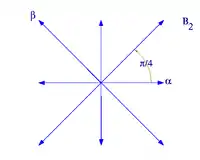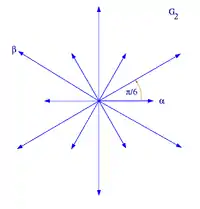根系 B2	根系 G2

當 ${\displaystyle \Phi }$ 是 ${\displaystyle V}$ 中的根系，而 ${\displaystyle W}$ 是 ${\displaystyle \Psi =\Phi \cap W}$ 在 ${\displaystyle W}$ 中生成的子空間，則 ${\displaystyle \Psi }$ 是 ${\displaystyle W}$ 中的根系。因此上述列表限制了任意秩根系中兩根的幾何關係，例如：任意兩根的交角僅可能是 ${\displaystyle 0,30,45,60,90,120,135,150}$ 或 ${\displaystyle 180}$ 度。

取 ${\displaystyle V}$ 為 ${\displaystyle \mathbb {R} ^{n+1}}$ 中滿足 ${\displaystyle \sum _{i=1}^{n+1}x_{i}=0}$ 的點 ${\displaystyle (x_{1},\ldots ,x_{n+1})}$ 所成之子空間。令 ${\displaystyle \Phi }$ 為 ${\displaystyle V}$ 中長度為 ${\displaystyle {\sqrt {2}}}$ 的格子點。取 ${\displaystyle \mathbb {R} ^{n+1}}$ 的標準基 ${\displaystyle e_{1},\ldots ,e_{n+1}}$，則根具有 ${\displaystyle e_{i}-e_{j}\;(i\neq j)}$ 的形式，共有 ${\displaystyle n(n+1)}$ 個根。通常取單根為 ${\displaystyle \alpha _{i}:=e_{i}-e_{i+1}}$。

對垂直於 ${\displaystyle \alpha _{i}}$ 的超平面的鏡射在 ${\displaystyle \Phi }$ 上的作用是交換第 ${\displaystyle i,i+1}$ 個座標。因此 ${\displaystyle A_{n}}$ 的外爾群不外就是對稱群 ${\displaystyle S_{n+1}}$。

${\displaystyle A_{n}}$ 是李代數 ${\displaystyle {\mathfrak {sl}}(n+1,\mathbb {C} )}$ 的根系。

取 ${\displaystyle V=\mathbb {R} ^{n}}$，並令 ${\displaystyle \Phi }$ 為 ${\displaystyle V}$ 中長度為 ${\displaystyle 1,{\sqrt {2}}}$ 的格子點。共有 ${\displaystyle 2n^{2}}$ 個根。通常取單根為 ${\displaystyle \alpha _{i}=e_{i}-e_{i+1}\;(1\leq i<n)}$ 及 ${\displaystyle \alpha _{n}:=e_{n}}$（短根）。

對短根 ${\displaystyle \alpha _{n}}$ 的反射即 ${\displaystyle (x_{1},\ldots ,x_{n})\mapsto (x_{1},\ldots ,-x_{n})}$。

${\displaystyle B_{1}}$ 跟 ${\displaystyle A_{1}}$ 僅差一個縮放，因此通常僅考慮 ${\displaystyle n\geq 2}$ 的情形。${\displaystyle B_{n}}$ 是李代數 ${\displaystyle {\mathfrak {so}}(2n+1,\mathbb {C} )}$ 的根系。

取 ${\displaystyle V=\mathbb {R} ^{n}}$，${\displaystyle \Phi }$ 為 ${\displaystyle V}$ 中所有長度 ${\displaystyle {\sqrt {2}}}$ 的格子點與形如 ${\displaystyle 2\lambda }$的點，其中 ${\displaystyle \lambda }$ 是長度為一的格子點。共有 ${\displaystyle 2n^{2}}$ 個根。通常取單根為 ${\displaystyle \alpha _{i}:=e_{i}-e_{i+1}\;(1\leq i<n)}$及 ${\displaystyle \alpha _{n}:=2e_{n}}$（長根）。

${\displaystyle C_{2}}$ 與 ${\displaystyle B_{2}}$ 僅差一個縮放加上旋轉 45 度，因此通常僅考慮 ${\displaystyle n\geq 3}$ 的情形。${\displaystyle C_{n}}$ 是李代數 ${\displaystyle {\mathfrak {sp}}(2n,\mathbb {C} )}$ 的根系。

取 ${\displaystyle V:=\mathbb {R} ^{n}}$，${\displaystyle \Phi }$ 為 ${\displaystyle V}$ 中長度 ${\displaystyle {\sqrt {2}}}$ 的格子點。共有 ${\displaystyle 2n(n-1)}$ 個根。通常取單根為 ${\displaystyle \alpha _{i}=e_{i}-e_{i+1},\;(1\leq i<n)}$ 及 ${\displaystyle \alpha _{n}=e_{n}+e_{n-1}}$。

${\displaystyle D_{3}}$ 同構於 ${\displaystyle A_{3}}$，故通常僅考慮 ${\displaystyle n\geq 4}$ 的情形。${\displaystyle D_{n}}$ 是李代數 ${\displaystyle {\mathfrak {so}}(2n,\mathbb {C} )}$ 的根系。

${\displaystyle E_{8}}$ 是較為特殊的根系。首先定義 ${\displaystyle \mathbb {R} ^{8}}$ 中滿足下述條件的點集 ${\displaystyle \Gamma _{8}}$：

• 各座標均為整數，或均為半整數（不容相混）。
• 八個座標的和為偶數。

定義 ${\displaystyle E_{8}}$ 為 ${\displaystyle \Gamma _{8}}$ 中長度為 ${\displaystyle {\sqrt {2}}}$ 的向量，即：

${\displaystyle \left\{\alpha \in \mathbb {Z} ^{8}\sqcup \left(\mathbb {Z} +{\frac {1}{2}}\right)^{8}:|\alpha |^{2}=2,\;\sum \alpha _{i}\in 2\mathbb {Z} \right\}}$

定義 ${\displaystyle E_{7}}$ 為 ${\displaystyle E_{8}}$ 與超平面 ${\displaystyle \{x:(x,\alpha )=0\}}$ 之交， 其中 ${\displaystyle \alpha \in E_{8}}$ 是任取的根。同樣步驟施於 ${\displaystyle E_{7}}$，得到更小的根系 ${\displaystyle E_{6}}$。根系 ${\displaystyle E_{6},E_{7},E_{8}}$ 分別有 72, 126 與 240 個根。若續行此化約步驟，則會得到典型根系 ${\displaystyle D_{5},A_{4}}$。

另一種等價的描述是取 ${\displaystyle \Gamma '_{8}}$ 為：

• 各坐標均為整數，而且其和為偶數；或
• 各坐標均為半整數，而且其和為奇數。

${\displaystyle \Gamma _{8}}$ 與 ${\displaystyle \Gamma '_{8}}$ 同構。將任意偶數個座標乘以負一，便可在兩者間轉換。${\displaystyle \Gamma _{8}}$ 稱為 ${\displaystyle E_{8}}$ 的偶坐標系，${\displaystyle \Gamma '_{8}}$ 稱為奇坐標系。

在偶坐標下，通常取單根為

${\displaystyle \alpha _{i}:=e_{i}-e_{i+1}\quad (1\leq i\leq 6)}$

${\displaystyle \alpha _{7}:=e_{7}+e_{6}}$

${\displaystyle \alpha _{8}=\beta _{0}={\frac {\sum _{i=1}^{8}e_{i}}{2}}}$

在奇坐標下，通常取單根為

${\displaystyle \alpha _{i}:=e_{i}-e_{i+1}\quad (1\leq i\leq 7)}$

${\displaystyle \alpha _{8}:=\beta _{5}}$，其中

${\displaystyle \beta _{j}:={\frac {-\sum _{i=1}^{j}e_{i}+\sum _{i=j+1}^{8}e_{i}}{2}}}$

（在上述定義中，若改取 ${\displaystyle \beta _{3}}$，將得到同構的結果。若改取 ${\displaystyle \beta _{1},\beta _{7},\beta _{2},\beta _{6}}$，將得到 ${\displaystyle A_{8}}$ 或 ${\displaystyle D_{8}}$。至於 ${\displaystyle \beta _{4}}$，其坐標和為零，而 ${\displaystyle \alpha _{1},\ldots ,\alpha _{7}}$ 亦然，所以張出的向量空間維度不合所求。

刪去 ${\displaystyle \alpha _{1}}$ 可得到 ${\displaystyle E_{7}}$ 的一組單根；再刪去 ${\displaystyle \alpha _{2}}$，可得 ${\displaystyle E_{6}}$ 的單根。

由於對 ${\displaystyle \alpha _{1}}$ 垂直等價於前兩個坐標相等，而對 ${\displaystyle \alpha _{1},\alpha _{2}}$ 垂直等價於前三個座標相等，不難導出 ${\displaystyle E_{7},E_{6}}$ 的明確定義：

E₇ = (α ∈ Z⁷ ∪ (Z+½)⁷: ∑α_i² + α₁² = 2，∑α_i + α₁ ∈ 2Z),

E₆ = (α ∈ Z⁶ ∪ (Z+½)⁶: ∑α_i² + 2α₁² = 2，∑α_i + 2α₁ ∈ 2Z)

對於 ${\displaystyle F_{4}}$，取 ${\displaystyle V=\mathbb {R} ^{4}}$，並令 ${\displaystyle \Phi }$ 為滿足下述條件的向量：

• ${\displaystyle |\alpha |=1,{\sqrt {2}}}$
• ${\displaystyle 2\alpha }$ 各坐標皆為奇數或皆為偶數。

此根系有 ${\displaystyle 48}$ 個根。通常取單根為 ${\displaystyle B_{3}}$ 的單根再加上 ${\displaystyle \alpha _{4}=-\left(\sum _{i=1}^{4}e_{i}\right)/2}$。

${\displaystyle G_{2}}$ 有 12 個根，構成一個六邊形的頂點，詳如秩二的例子一節所示。通常取單根為

• ${\displaystyle \alpha _{1}}$
• ${\displaystyle \beta$ :=\alpha _{2}-\alpha _{1}}

在此沿用了之前的符號： ${\displaystyle \alpha _{i}:=e_{i}-e_{i+1},\;(i=1,2)}$。