桥 (图论)
在圖論中,一條邊被稱為「橋」代表這條邊一旦被刪除,這張圖的連通塊數量會增加。[1] 等價地說,一條邊是一座橋若且唯若這條邊不在任何環上。一張圖可以有零或多座橋。
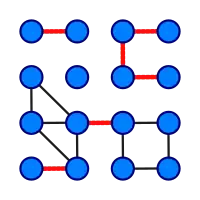
這是有16個頂點和6個橋的圖(橋以紅色線段標示)

沒有橋的無向連通圖
Tarjan的找橋演算法
注释
- Bollobás, Béla, , Graduate Texts in Mathematics 184, New York: Springer-Verlag: 6, 1998 [2015-09-17], ISBN 0-387-98488-7, MR 1633290, doi:10.1007/978-1-4612-0619-4, (原始内容存档于2018-05-05).
- Robbins, H. E., , 美国数学月刊, 1939, 46: 281–283, doi:10.2307/2303897, hdl:10338.dmlcz/101517
 .
. - Tarjan, R. Endre, , Information Processing Letters: 160–161, MR 0349483, doi:10.1016/0020-0190(74)90003-9.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.