瑞利衰落信道

瑞利衰落信道（英語：）是一种无线电信号传播环境的“统计模型（statistical model）”。这种模型假设信号通过无线信道之后，其信号幅度（amplitude）是随机的，即“衰落(fading)”，并且其包络（envelope）服从瑞利分布（Rayleigh distribution）。

这一信道模型能够描述由电离层和对流层反射的短波信道，以及建筑物密集的城市环境。[1][2]瑞利衰落只适用于从发射机到接收机不存在直射信号（LoS，Line of Sight）的情况，否则应使用莱斯衰落信道（Rician fading channel）作为信道模型。

模型

瑞利衰落能有效描述存在能够大量散射无线电信号的障碍物的无线传播环境。若传播环境中存在足够多的散射，则冲激信号到达接收机后表现为大量统计独立的随机变量的叠加，根据中心极限定理，则这一无线信道的冲激响应将是一个高斯过程。如果这一散射信道中不存在主要的信号分量，通常这一条件是指不存在直射信号（LoS），则这一过程的均值为0，且相位服从0 到2π 的均匀分布。即，信道响应的包络服从瑞利分布。设随机变量R，于是其概率密度函数为：

p_{R}(r)={\frac {2r}{\sigma }}e^{-r^{2}/\sigma },\ r\geq {}0

其中

\sigma =E(R^{2})

。

若信道中存在一主要分量，例如直射信号（LoS），则信道响应的包络服从莱斯分布，对应的信道模型为莱斯衰落信道。

通常将信道增益以等效基带信号表示，即用一复数表示信道的幅度和相位特性。由此瑞利衰落即可由这一复数表示，它的实部和虚部服从于零均值的独立同分布高斯过程。

模型的适用

最大多普勒频移为10Hz的瑞利衰落信道。

最大多普勒频移为100Hz的瑞利衰落信道。

瑞利衰落模型适用于描述建筑物密集的城镇中心地带的无线信道。密集的建筑和其他物体使得无线设备的发射机和接收机之间没有直射路径，而且使得无线信号被衰减、反射、折射、衍射。在曼哈顿的实验证明，当地的无线信道环境确实接近于瑞利衰落。[3] 通过电离层和对流层反射的无线电信道也可以用瑞利衰落来描述，因为大气中存在的各种粒子能够将无线信号大量散射。

瑞利衰落属于小尺度的衰落效应，它总是叠加于如阴影、衰减等大尺度衰落效应上。

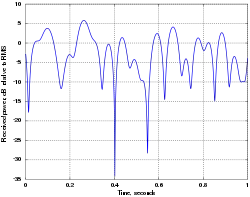
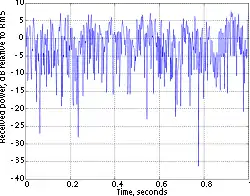
信道衰落的快慢与发射端和接收端的相对运动速度的大小有关。相对运动导致接收信号的多普勒频移。图中所示即为一固定信号通过单径的瑞利衰落信道后，在1秒内的能量波动，这一瑞利衰落信道的多普勒频移最大分别为10Hz和100Hz，在GSM1800MHz的载波频率上，其相应的移动速度分别为约6千米每小时和60千米每小时。特别需要注意的是信号的“深衰落”现象，此时信号能量的衰减达到数千倍，即30～40分贝。

幅度穿越率

幅度穿越率（LCR，level crossing rate）是对衰落快慢的一种度量。LCR 给出衰落信号的幅度以怎样的频率穿越某一门限，通常按照正向穿越方向进行计算。瑞利衰落的LCR为：[5]

LCR={\sqrt {2\pi }}f_{d}\rho e^{-\rho ^{2}}

其中 $f_{d}$ 是最大多普勒频偏， $\,\!\rho$ 为对信号的均方根进行归一化的信号门限值：

\rho ={\frac {R_{thresh}}{R_{rms}}}

.

平均衰落时间

平均衰落时间（AFD，average fade duration）这一参数是指信号在门限 $\,\!\rho$ 以下持续的时间。瑞利衰落的平均衰落时间为：[5]

AFD={\frac {e^{\rho ^{2}}-1}{\rho f_{d}{\sqrt {2\pi }}}}

.

幅度穿越速率和平均衰落时间这两个参数给出了衰落在时间上严重程度的描述。对于一定的门限值 $\rho$ ，平均衰落时间和幅度穿越速率的积为常数，并且可以表示为：

AFD\times LCR=1-e^{-\rho ^{2}}

.