破碎對角線
破碎對角線是娛樂數學以及線性代數中的名詞,是指三階或三階以上方陣中和對角線平行的二條線,若越過方陣的邊界,可以將二段對角線連接成一條和對角線平行的線。 如以下的方陣中,星號組成的就是破碎對角線。
| * | ||
| * | ||
| * |
泛對角幻方
若幻方中的每一條破碎對角線的和,和各行、各列及主對角線的和相同,即稱為泛對角幻方[1][2]
以下即為一個泛對角幻方的例子。
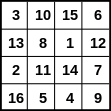
可以檢查所有的破碎對角線,其和都相同,即可知道是泛對角幻方:
- 3+12+14+5 = 34
- 10+1+7+16 = 34
- 10+13+7+4 = 34
有一種視覺化破碎對角線的方式,是在幻方旁邊放一個輔助的幻方。


像破碎對角線{3, 12, 14, 5},環繞原始的幻方,可以視為從右邊幻方的左上角,往左下延伸。
線性代數
在3階行列式的公式中,也有用到破碎對角線。
對於3 × 3矩陣A,其行列式為
此處, and 都是破碎對角線元素的乘積。
在3階行列式的計算中,會用到破碎對角線,這可以用在計算行列式中,用到矩陣的子式來證明。
參考資料
- Pickover, Clifford A., , Princeton University Press: 7, 2011, ISBN 9781400841516.
- Licks, H. E., , D. Van Nostrand Company: 42, 1921.
- title=Determinant|url=https://mathworld.wolfram.com/Determinant.html (页面存档备份,存于)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.