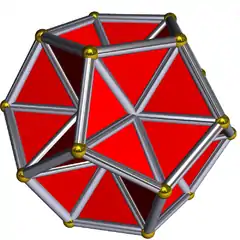
第六星形二十面體
第六星形二十面體是正二十面體的一種星形化體，為正二十面體的面向外延伸並相交所形成的第六種立體，外觀看起來像是部分面凹陷的正十二面體，並且每個凹陷處都有一個五角錐狀尖刺向外突出[1]。
 | |||||||||||||
| 類別 | 星形二十面體 收錄於《五十九種二十面體》中 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 識別 | |||||||||||||
| 名稱 | 第六星形二十面體 | ||||||||||||
| 參考索引 | W31, 23/59 | ||||||||||||
| 數學表示法 | |||||||||||||
| 杜瓦表示法 | Fg1 | ||||||||||||
| 對稱性 | |||||||||||||
| 對稱群 | Ih | ||||||||||||
| 圖像 | |||||||||||||
| |||||||||||||
性質
第六星形二十面體由十對平行的面組成[1]，每個面皆會互相遮蔽，而每個面露在外面的部份有3個鳶形和3個凹五邊形[2]。若將每個可見部分視為一個獨立的面，則這個立體共有120個面，可分為60個為內凹的部分和60個構成向外尖角的面[3]。這樣的結構在杜瓦記號中可以用Fg1來表示，[4]這代表其包含了星形二十面體中的F胞和g1胞（G層子胞），即從中間數來的第8、第9和第12個胞。[5]
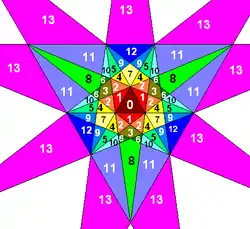 星形二十面體中的胞 |
 構成第六星形二十面體的面 |
相關多面體
部分最外層為f2g1的星形二十面體也具有相似的形狀：[4]
| 名稱 | 杜瓦記號 | 星狀圖 | 立體圖 |
|---|---|---|---|
| 第六星形二十面體 23 （《五十九種二十面體》） 17（惠勒） |
Fg1 | |
|
| 50 （《五十九種二十面體》） | Ef1g1 |  |  |
| 54 （《五十九種二十面體》） | e2f1f2g1 |  |  |
| 55 （《五十九種二十面體》） | De2f1f2g1 |  |  |
| 56 （《五十九種二十面體》） | Ef1f2g1 |  |  |
e1f1g1星形二十面體
 | ||
| 類別 | 星形二十面體 收錄於《五十九種二十面體》中 | |
|---|---|---|
| 識別 | ||
| 名稱 | e1f1g1星形二十面體 | |
| 參考索引 | 13/59 | |
| 數學表示法 | ||
| 杜瓦表示法 | e1f1g1 | |
| 組成與佈局 | ||
| 面的種類 |  | |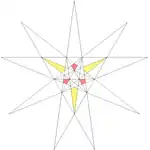
| 對稱性 | ||
| 對稱群 | Ih | |
| 圖像 | ||
| ||
第六星形二十面體可以視為將f2星形二十面體嵌入到e1f1g1星形二十面體中構成。[4]:18
e1f1g1星形二十面體
f2星形二十面體
第六星形二十面體
e1f1g1星形二十面體外觀類似一個中心挖空並破洞的凹五角錐十二面體[4]:21。組成這個立體的星形二十面體胞為第3、第6、第9和第12個胞。[7]
星形二十面體中的胞 |
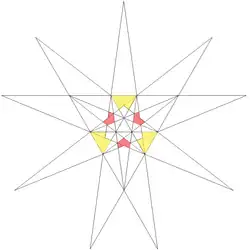 構成e1f1g1星形二十面體的面 |
有另一種杜瓦記號也記為e1f1g1的星形二十面體，其組成胞為第3胞、左側的第5胞、右側的第6胞、左側的第9胞、右側的第10胞和第12胞組成。[8]為了區別，通常會透過粗體來表示其所代表的胞層的差異。另外這種立體有收錄於溫尼爾的多面體模型中，為其描述的第十四種星形二十面體。
- e1f1g1星形二十面體
參見
- 《五十九種二十面體》
參考文獻
- Jenkins, G. and Bear, M. . Advanced Polyhedra. Tarquin Publications. 2004. ISBN 9781899618620.
- . How-to-Build-Polyhedra. [2021-09-01]. （原始内容存档于2022-05-31）.
- Jenkins, G. and Bear, M. . Tarquin polyhedra. Tarquin Publications. 1985. ISBN 978-0906212462.
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F., 3rd, Tarquin, 1999, ISBN 978-1-899618-32-3, MR 0676126 p. 259 (1st Edn University of Toronto (1938))
- . mathconsult.ch. [2021-09-01]. （原始内容存档于2022-05-31）.
- Wenninger, M.J. . Cambridge University Press. 1974 [2021-09-01]. ISBN 9780521098595. LCCN 69010200. （原始内容存档于2021-08-31）.
- . mathconsult.ch. [2021-09-01]. （原始内容存档于2022-05-30）.
- . mathconsult.ch. [2021-09-01]. （原始内容存档于2022-05-31）.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.