經典力學方程列表

經典力學是物理學描述宏觀物體運動的分支。[1]是最熟悉的物理學理論。涵蓋如常用和已知的加速度和力。[2]本列表基於具固定軸的三維歐幾里得空間參考系。三軸的交點稱為此空間的原點。[3]

經典力學概念包括微分方程、流形、李群和遍歷理論。各種物理量相互關聯[4]。本列表總結了其中最重要的內容。

本文列出了牛頓力學的方程，有關經典力學（包括拉格朗日力學和哈密頓力學）的更一般公式，請參閱分析力學。

經典力學

質量與慣量

通用名	通用符號	定義	國際單位制	量綱
線/表面/體積質量密度	λ或μ用於線密度（μ主要用在声学），σ用於表面，ρ用於體積。	$m=\int \lambda \,\mathrm {d} \ell$ $m=\iint \sigma \,\mathrm {d} S$ $m=\iiint \rho \,\mathrm {d} V$	kg m⁻ⁿ, n = 1, 2, 3	M L⁻ⁿ
質量矩[5]	m （沒有通用符號）	點質量： $\mathbf {m} =\mathbf {r} m$ 相對固定軸 $x_{i}$ 的離散質量： $\mathbf {m} =\sum _{i=1}^{N}\mathbf {r} _{i}m_{i}$ 相對固定軸 $x_{i}$ 的連續質量： $\mathbf {m} =\int \rho \left(\mathbf {r} \right)x_{i}\mathrm {d} \mathbf {r}$	kg m	M L
質心	r_com （符號不一定）	第i個質量 $\mathbf {m} _{i}=\mathbf {r} _{i}m_{i}$ 離散質量： $\mathbf {r} _{\mathrm {com} }={\frac {1}{M}}\sum _{i}\mathbf {r} _{i}m_{i}={\frac {1}{M}}\sum _{i}\mathbf {m} _{i}$ 連續質量： $\mathbf {r} _{\mathrm {com} }={\frac {1}{M}}\int \mathrm {d} \mathbf {m} ={\frac {1}{M}}\int \mathbf {r} \,\mathrm {d} m={\frac {1}{M}}\int \mathbf {r} \rho \,\mathrm {d} V$	m	L
二體約化質量	m₁₂, μ= m₁ and m₂	$\mu ={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}$	kg	M
轉動慣量（MOI）	I	離散質量： $I=\sum _{i}\mathbf {m} _{i}\cdot \mathbf {r} _{i}=\sum _{i}\left\|\mathbf {r} _{i}\right\|^{2}m$ 連續質量： $I=\int \left\|\mathbf {r} \right\|^{2}\mathrm {d} m=\int \mathbf {r} \cdot \mathrm {d} \mathbf {m} =\int \left\|\mathbf {r} \right\|^{2}\rho \,\mathrm {d} V$	kg m²	M L²

導出的運動學物理量

經典粒子的運動學物理量：質量m、位置r、速度v、加速度a

通用名	通用符號	定義	國際單位制	量綱
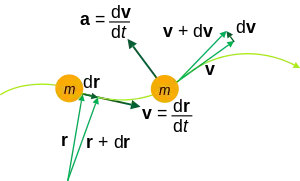
速度	v	$\mathbf {v} ={\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}$	m s⁻¹	L T⁻¹
加速度	a	$\mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}$	m s⁻²	L T⁻²
加加速度	j	$\mathbf {j} ={\frac {\mathrm {d} \mathbf {a} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{3}\mathbf {r} }{\mathrm {d} t^{3}}}$	m s⁻³	L T⁻³
Jounce	s	$\mathbf {s} ={\frac {\mathrm {d} \mathbf {j} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{4}\mathbf {r} }{\mathrm {d} t^{4}}}$	m s⁻⁴	L T⁻⁴
角速度	ω	${\boldsymbol {\omega }}=\mathbf {\hat {n}} {\frac {\mathrm {d} \theta }{\mathrm {d} t}}$	rad s⁻¹	T⁻¹
角加速度	α	${\boldsymbol {\alpha }}={\frac {\mathrm {d} {\boldsymbol {\omega }}}{\mathrm {d} t}}=\mathbf {\hat {n}} {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}$	rad s⁻²	T⁻²
角加加速度	ζ	${\boldsymbol {\zeta }}={\frac {\mathrm {d} {\boldsymbol {\alpha }}}{\mathrm {d} t}}=\mathbf {\hat {n}} {\frac {\mathrm {d} ^{3}\theta }{\mathrm {d} t^{3}}}$	rad s⁻³	T⁻³

導出的動力學物理量

經典力學下物質的角動量。

左：固有的自旋角動量S是物體每一點的軌道角動量

右：對應一個軸的外在軌道角動量L

上：轉動慣量 I以及角速度ω（L不一定會和ω平行）[6]

下：動量p以及其相對於軸的位置r

。總角動量（spin + orbital）為J

通用名	通用符號	定義	國際單位制	量綱
动量	p	$\mathbf {p} =m\mathbf {v}$	kg m s⁻¹	M L T⁻¹
力	F	$\mathbf {F} =\mathrm {d} \mathbf {p} /\mathrm {d} t$	N = kg m s⁻²	M L T⁻²
冲量	J, Δp, I	$\mathbf {J} =\Delta \mathbf {p} =\int _{t_{1}}^{t_{2}}\mathbf {F} \,\mathrm {d} t$	kg m s⁻¹	M L T⁻¹
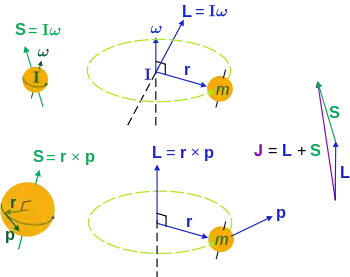
相對一點r₀的角动量	L, J, S	$\mathbf {L} =\left(\mathbf {r} -\mathbf {r} _{0}\right)\times \mathbf {p}$ 若各質點的旋轉軸均相交在同一點，可以設定r₀ = 0。	kg m² s⁻¹	M L² T⁻¹
力相對一點r₀的力矩	τ, M	${\boldsymbol {\tau }}=\left(\mathbf {r} -\mathbf {r} _{0}\right)\times \mathbf {F} ={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}$	N m = kg m² s⁻²	M L² T⁻²
角衝量	ΔL （沒有通用符號）	$\Delta \mathbf {L} =\int _{t_{1}}^{t_{2}}{\boldsymbol {\tau }}\,\mathrm {d} t$	kg m² s⁻¹	M L² T⁻¹

一般能量定義

通用名	通用符號	定義	國際單位制	量綱
合力産生的功	W	$W=\int _{C}\mathbf {F} \cdot \mathrm {d} \mathbf {r}$	J = N m = kg m² s⁻²	M L² T⁻²
力學系統所作的功	W_ON, W_BY	$\Delta W_{\mathrm {ON} }=-\Delta W_{\mathrm {BY} }$	J = N m = kg m² s⁻²	M L² T⁻²
勢能	φ, Φ, U, V, E_p	$\Delta W=-\Delta V$	J = N m = kg m² s⁻²	M L² T⁻²
機械功率	P	$P={\frac {\mathrm {d} E}{\mathrm {d} t}}$	W = J s⁻¹	M L² T⁻³

每一個保守力都有對應的势能。根據以下二個原理，可以設定勢能U的值：

保守力為零的時候，勢能也定義為零。
保守力作功時，勢能減少。

廣義力學

通用名	通用符號	定義	國際單位制	量綱
廣義座標	q, Q		不一定	不一定
廣義速度	${\dot {q}},{\dot {Q}}$	${\dot {q}}\equiv \mathrm {d} q/\mathrm {d} t$	不一定	不一定
廣義動量	p, P	$p=\partial L/\partial {\dot {q}}$	不一定	不一定
拉格朗日量	L	$L(\mathbf {q} ,\mathbf {\dot {q}} ,t)=T(\mathbf {\dot {q}} )-V(\mathbf {q} ,\mathbf {\dot {q}} ,t)$ 其中 $\mathbf {q} =\mathbf {q} (t)$ 以及 p = p(t) 分別是廣義座標以及動量的向量，是時間的函數。	J	M L² T⁻²
哈密顿量	H	$H(\mathbf {p} ,\mathbf {q} ,t)=\mathbf {p} \cdot \mathbf {\dot {q}} -L(\mathbf {q} ,\mathbf {\dot {q}} ,t)$	J	M L² T⁻²
作用量，哈密頓主函數	S, $\scriptstyle {\mathcal {S}}$	${\mathcal {S}}=\int _{t_{1}}^{t_{2}}L(\mathbf {q} ,\mathbf {\dot {q}} ,t)\mathrm {d} t$	J s	M L² T⁻¹

運動學

在以下轉動的定義中，角度是對應轉動軸的位意角度。一般常用θ，不過不一定要是極座標下的極角。單位軸向量

\mathbf {\hat {n}} =\mathbf {\hat {e}} _{r}\times \mathbf {\hat {e}} _{\theta }

定義轉動軸 $\scriptstyle \mathbf {\hat {e}} _{r}$ 為 $r$ 方向上的單位向量， $\scriptstyle \mathbf {\hat {e}} _{\theta }$ 是和角呈切線的單位向量。

	平移	轉動
速度	平均： $\mathbf {v} _{\mathrm {average} }={\Delta \mathbf {r} \over \Delta t}$ 瞬時： $\mathbf {v} ={d\mathbf {r} \over dt}$	角速度 ${\boldsymbol {\omega }}=\mathbf {\hat {n}} {\frac {{\rm {d}}\theta }{{\rm {d}}t}}$ 轉動刚体： $\mathbf {v} ={\boldsymbol {\omega }}\times \mathbf {r}$
加速度	平均： $\mathbf {a} _{\mathrm {average} }={\frac {\Delta \mathbf {v} }{\Delta t}}$ 瞬時： $\mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{2}\mathbf {r} }{dt^{2}}}$	角加速度 ${\boldsymbol {\alpha }}={\frac {{\rm {d}}{\boldsymbol {\omega }}}{{\rm {d}}t}}=\mathbf {\hat {n}} {\frac {{\rm {d}}^{2}\theta }{{\rm {d}}t^{2}}}$ 轉動刚体： $\mathbf {a} ={\boldsymbol {\alpha }}\times \mathbf {r} +{\boldsymbol {\omega }}\times \mathbf {v}$
加加速度	平均： $\mathbf {j} _{\mathrm {average} }={\frac {\Delta \mathbf {a} }{\Delta t}}$ 瞬時： $\mathbf {j} ={\frac {d\mathbf {a} }{dt}}={\frac {d^{2}\mathbf {v} }{dt^{2}}}={\frac {d^{3}\mathbf {r} }{dt^{3}}}$	角加加速度 ${\boldsymbol {\zeta }}={\frac {{\rm {d}}{\boldsymbol {\alpha }}}{{\rm {d}}t}}=\mathbf {\hat {n}} {\frac {{\rm {d}}^{2}\omega }{{\rm {d}}t^{2}}}=\mathbf {\hat {n}} {\frac {{\rm {d}}^{3}\theta }{{\rm {d}}t^{3}}}$ 轉動刚体： $\mathbf {j} ={\boldsymbol {\zeta }}\times \mathbf {r} +{\boldsymbol {\alpha }}\times \mathbf {a}$

動力學

	平移	轉動
动量	$\mathbf {p} =m\mathbf {v}$ 針對轉動剛體： $\mathbf {p} ={\boldsymbol {\omega }}\times \mathbf {m}$	角动量 $\mathbf {L} =\mathbf {r} \times \mathbf {p} =\mathbf {I} \cdot {\boldsymbol {\omega }}$ 此外積為赝矢量，若r和p都反向（變號），L不會變號。一般來說，I是二維張量，·表示張量縮並。
力和牛顿第二运动定律	作用在系統質心上的合力，等於動量的變化率： ${\begin{aligned}\mathbf {F} &={\frac {d\mathbf {p} }{dt}}={\frac {d(m\mathbf {v} )}{dt}}\\&=m\mathbf {a} +\mathbf {v} {\frac {{\rm {d}}m}{{\rm {d}}t}}\\\end{aligned}}$ 針對許多質點的系統，質點i的運動方程式為：[7] ${\frac {\mathrm {d} \mathbf {p} _{i}}{\mathrm {d} t}}=\mathbf {F} _{E}+\sum _{i\neq j}\mathbf {F} _{ij}$ 其中p_i是第i個質點的動量，F_ij，是粒子j作用在粒子i上的力，F_E是合外力（來自系統以外的物體）。粒子i不會產生給自身的力。	力矩力矩（torque）τ也稱為moment of a force，是轉動系統中對應力的物理量：[8] ${\boldsymbol {\tau }}={\frac {{\rm {d}}\mathbf {L} }{{\rm {d}}t}}=\mathbf {r} \times \mathbf {F} ={\frac {{\rm {d}}(\mathbf {I} \cdot {\boldsymbol {\omega }})}{{\rm {d}}t}}$ 若是剛體，牛頓第二轉動定律的形式類似平移運動下的形式： ${\begin{aligned}{\boldsymbol {\tau }}&={\frac {{\rm {d}}\mathbf {L} }{{\rm {d}}t}}={\frac {{\rm {d}}(\mathbf {I} \cdot {\boldsymbol {\omega }})}{{\rm {d}}t}}\\&={\frac {{\rm {d}}\mathbf {I} }{{\rm {d}}t}}\cdot {\boldsymbol {\omega }}+\mathbf {I} \cdot {\boldsymbol {\alpha }}\\\end{aligned}}$ 若針對許多質點，質點i的運動方程為：[9] ${\frac {\mathrm {d} \mathbf {L} _{i}}{\mathrm {d} t}}={\boldsymbol {\tau }}_{E}+\sum _{i\neq j}{\boldsymbol {\tau }}_{ij}$
Yank	Yank是力的變化率： ${\begin{aligned}\mathbf {Y} &={\frac {d\mathbf {F} }{dt}}={\frac {d^{2}\mathbf {p} }{dt^{2}}}={\frac {d^{2}(m\mathbf {v} )}{dt^{2}}}\\[1ex]&=m\mathbf {j} +\mathbf {2a} {\frac {{\rm {d}}m}{{\rm {d}}t}}+\mathbf {v} {\frac {{\rm {d^{2}}}m}{{\rm {d}}t^{2}}}\end{aligned}}$ 若是固定質量，會變成下式： $\mathbf {Y} =m\mathbf {j}$	Rotatum Rotatum Ρ也稱為moment of a Yank，因為是是轉動系統中對應Yank的物理量： ${\boldsymbol {\mathrm {P} }}={\frac {{\rm {d}}{\boldsymbol {\tau }}}{{\rm {d}}t}}=\mathbf {r} \times \mathbf {Y} ={\frac {{\rm {d}}(\mathbf {I} \cdot {\boldsymbol {\alpha }})}{{\rm {d}}t}}$
衝量	衝量是動量的變化： $\Delta \mathbf {p} =\int \mathbf {F} \,dt$ 針對固定力F： $\Delta \mathbf {p} =\mathbf {F} \Delta t$	Twirl或是角衝量是角動量的變化： $\Delta \mathbf {L} =\int {\boldsymbol {\tau }}\,dt$ 針對固定力矩τ： $\Delta \mathbf {L} ={\boldsymbol {\tau }}\Delta t$

進動

陀螺的進動角速度為：

{\boldsymbol {\Omega }}={\frac {wr}{I{\boldsymbol {\omega }}}}

其中w是自旋物體的重量。

能量

系統以外事物對系統所作的機械功等於系統的動能變化：

通用功—能定理（平移及轉動）

系統以外事物，對曲線路徑C上的質點產生力F（在 r的位置）以及力矩τ，所做成的功W為：

W=\Delta T=\int _{C}\left(\mathbf {F} \cdot \mathrm {d} \mathbf {r} +{\boldsymbol {\tau }}\cdot \mathbf {n} \,{\mathrm {d} \theta }\right)

其中θ是相對单位向量n所定義軸的轉動角度。

動能

物體一開始的速度為 $v_{0}$ ，後來的速度為 $v$ ，其动能變化為：

\Delta E_{k}=W={\frac {1}{2}}m(v^{2}-{v_{0}}^{2})

彈性勢能

遵守胡克定律的彈簧，若一端固定，拉長後，其彈性勢能為

\Delta E_{p}={\frac {1}{2}}k(r_{2}-r_{1})^{2}

其中r₂和r₁是彈簧未固定端，在拉長後以及拉長前的共線座標，方向是往拉長／壓縮的方向，k是彈簧常數。

剛體運動的欧拉方程

萊昂哈德·歐拉也像牛頓一様，發表了運動定律，可以參見歐拉運動定律。這些定律將牛頓運動定律擴展到剛體的運動上，不過本質是相同的。以下是歐拉提出新的運動方程式[10]：

\mathbf {I} \cdot {\boldsymbol {\alpha }}+{\boldsymbol {\omega }}\times \left(\mathbf {I} \cdot {\boldsymbol {\omega }}\right)={\boldsymbol {\tau }}

其中I是轉動慣量張量.

通用平面運動

前面平面運動的方程可以用在此處，應用上述的定義即可推出動量、角動量等。針對在平面上路徑移動的物體。

\mathbf {r} =\mathbf {r} (t)=r\mathbf {\hat {e}} _{r}

以下的結果可應用在質點上。

運動學	動力學
位置 $\mathbf {r} =\mathbf {r} \left(r,\theta ,t\right)=r\mathbf {\hat {e}} _{r}$
速度 $\mathbf {v} =\mathbf {\hat {e}} _{r}{\frac {\mathrm {d} r}{\mathrm {d} t}}+r\omega \mathbf {\hat {e}} _{\theta }$	動量 $\mathbf {p} =m\left(\mathbf {\hat {e}} _{r}{\frac {\mathrm {d} r}{\mathrm {d} t}}+r\omega \mathbf {\hat {e}} _{\theta }\right)$ 角動量 $\mathbf {L} =m\mathbf {r} \times \left(\mathbf {\hat {e}} _{r}{\frac {\mathrm {d} r}{\mathrm {d} t}}+r\omega \mathbf {\hat {e}} _{\theta }\right)$
加速度 $\mathbf {a} =\left({\frac {\mathrm {d} ^{2}r}{\mathrm {d} t^{2}}}-r\omega ^{2}\right)\mathbf {\hat {e}} _{r}+\left(r\alpha +2\omega {\frac {\mathrm {d} r}{{\rm {d}}t}}\right)\mathbf {\hat {e}} _{\theta }$	向心力為 $\mathbf {F} _{\bot }=-m\omega ^{2}R\mathbf {\hat {e}} _{r}=-\omega ^{2}\mathbf {m}$ 其中的m是質量矩（mass moment），科里奥利力為 $\mathbf {F} _{c}=2\omega m{\frac {{\rm {d}}r}{{\rm {d}}t}}\mathbf {\hat {e}} _{\theta }=2\omega mv\mathbf {\hat {e}} _{\theta }$ 科里奥利加速度以及科里奥利也可以寫成： $\mathbf {F} _{c}=m\mathbf {a} _{c}=-2m{\boldsymbol {\omega \times v}}$

連心力運動

針對質量較大的物體，而且因為其他物體所施加的連心力而運動，連心力只和二物體質心的距離有關，其運動方程為：

{\frac {d^{2}}{d\theta ^{2}}}\left({\frac {1}{\mathbf {r} }}\right)+{\frac {1}{\mathbf {r} }}=-{\frac {\mu \mathbf {r} ^{2}}{\mathbf {l} ^{2}}}\mathbf {F} (\mathbf {r} )

定加速度運動方程

僅當加速度恆定時才能使用這些方程式。如果加速度會變化，則必須使用上面的一般微積分學方程，透過積分位置、速度和加速度的定義來找到（見上文）。

線性運動	旋轉運動
$\mathbf {v-v_{0}} =\mathbf {a} t$	$\omega -\omega _{0}=\alpha t$
$\mathbf {x-x_{0}} ={\tfrac {1}{2}}(\mathbf {v_{0}+v} )t$	$\theta -\theta _{0}={\tfrac {1}{2}}(\omega _{0}+\omega )t$
$\mathbf {x-x_{0}} =\mathbf {v} _{0}t+{\tfrac {1}{2}}\mathbf {a} t^{2}$	$\theta -\theta _{0}=\omega _{0}t+{\tfrac {1}{2}}\alpha t^{2}$
$\mathbf {x} _{n^{th}}=\mathbf {v} _{0}+\mathbf {a} (n-{\tfrac {1}{2}})$	$\theta _{n^{th}}=\omega _{0}+\alpha (n-{\tfrac {1}{2}})$
$v^{2}-v_{0}^{2}=2\mathbf {a(x-x_{0})}$	$\omega ^{2}-\omega _{0}^{2}=2\alpha (\theta -\theta _{0})$

伽利略座標系變換

在古典（伽利略-牛頓）力學裡，將物理定律從一個慣性或加速（包括旋轉）坐標系（參考坐標系是以定速移動，其中包括零速）變換到另一個坐標系的變換即為伽利略變換。

以下標示r, v, a 的物理量是在坐標系F的位置、速度、加速度物理量，而標示r’, v’, a’ 的物理量是在以相對坐標系F移動速度V或是角速度Ω的坐標系F’的的位置、速度、加速度物理量。相對的，F是以相反的速度(—V or —Ω) 相對於F'移動。此情形類似相對加速度。

運動方式	慣性坐標系	加速坐標系
移動 V = 兩個慣性坐標系F和F'之間的相對定速度 A = 兩個加速坐標系F和F'之間的相對（變）加速度	相對位置 $\mathbf {r} '=\mathbf {r} +\mathbf {V} t$ 相對速度 $\mathbf {v} '=\mathbf {v} +\mathbf {V}$ 等效加速度 $\mathbf {a} '=\mathbf {a}$	相對加速度 $\mathbf {a} '=\mathbf {a} +\mathbf {A}$ 假想力 $\mathbf {F} '=\mathbf {F} -\mathbf {F} _{\mathrm {app} }$
轉動 Ω = 兩個慣性坐標系F和F'之間的相對定角速度 Λ = 兩個加速坐標系F和F'之間的相對（變）角加速度	相對角位置 $\theta '=\theta +\Omega t$ 相對速度 ${\boldsymbol {\omega }}'={\boldsymbol {\omega }}+{\boldsymbol {\Omega }}$ 等效加速度 ${\boldsymbol {\alpha }}'={\boldsymbol {\alpha }}$	相對加速度 ${\boldsymbol {\alpha }}'={\boldsymbol {\alpha }}+{\boldsymbol {\Lambda }}$ 假想力矩 ${\boldsymbol {\tau }}'={\boldsymbol {\tau }}-{\boldsymbol {\tau }}_{\mathrm {app} }$
轉動 Ω = 兩個慣性坐標系F和F'之間的相對定角速度 Λ = 兩個加速坐標系F和F'之間的相對（變）角加速度	將向量T轉換到旋轉座標系 ${\frac {{\rm {d}}\mathbf {T} '}{{\rm {d}}t}}={\frac {{\rm {d}}\mathbf {T} }{{\rm {d}}t}}-{\boldsymbol {\Omega }}\times \mathbf {T}$

機械諧振子

運動方程
物理情況	術語	平移方程	角方程
簡諧運動（SHM）	x = 橫向位移 θ = 角位移 A =橫向振幅 Θ = 角振幅	${\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-\omega ^{2}x$ 解： $x=A\sin \left(\omega t+\phi \right)$	${\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}=-\omega ^{2}\theta$ 解： $\theta =\Theta \sin \left(\omega t+\phi \right)$
非受迫阻尼振动	b = 阻尼常數 κ = 扭轉常數	${\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+b{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega ^{2}x=0$ 解（見下文ω）： $x=Ae^{-bt/2m}\cos \left(\omega '\right)$ 諧振頻率： $\omega _{\mathrm {res} }={\sqrt {\omega ^{2}-\left({\frac {b}{4m}}\right)^{2}}}$ 阻尼率： $\gamma =b/m$ 激發的預期壽命（Expected lifetime of excitation）： $\tau =1/\gamma$	${\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}+b{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\omega ^{2}\theta =0$ 解： $\theta =\Theta e^{-\kappa t/2m}\cos \left(\omega \right)$ 諧振頻率： $\omega _{\mathrm {res} }={\sqrt {\omega ^{2}-\left({\frac {\kappa }{4m}}\right)^{2}}}$ 阻尼率： $\gamma =\kappa /m$ 激發的預期壽命（Expected lifetime of excitation）： $\tau =1/\gamma$

角頻率
物理情況	術語	方程
線性無阻尼非受迫簡諧振子	k = 彈簧常數 m = 鐘擺質量	$\omega ={\sqrt {\frac {k}{m}}}$
線性非受迫阻尼諧振子	k = 彈簧常數 b = 阻尼係數	$\omega '={\sqrt {{\frac {k}{m}}-\left({\frac {b}{2m}}\right)^{2}}}$
低振幅角簡諧振子	I = 相對擺動軸轉動慣量 κ = 扭轉常數	$\omega ={\sqrt {\frac {\kappa }{I}}}$
低振幅單擺	L = 擺錘長度 g = 重力加速度 Θ = 角振幅	近似值 $\omega ={\sqrt {\frac {g}{L}}}$ 精確值可以表示成： $\omega ={\sqrt {\frac {g}{L}}}\left[1+\sum _{k=1}^{\infty }{\frac {\prod _{n=1}^{k}\left(2n-1\right)}{\prod _{n=1}^{m}\left(2n\right)}}\sin ^{2n}\Theta \right]$

機械振盪的能量
物理情況	術語	方程
簡諧運動能量	T = 動能 U = 勢能 E = 總能量	勢能： $U={\frac {m}{2}}\left(x\right)^{2}={\frac {m\left(\omega A\right)^{2}}{2}}\cos ^{2}(\omega t+\phi )$ 在x = A處的最大值： $U_{\mathrm {max} }{\frac {m}{2}}\left(\omega A\right)^{2}$ 動能： $T={\frac {\omega ^{2}m}{2}}\left({\frac {\mathrm {d} x}{\mathrm {d} t}}\right)^{2}={\frac {m\left(\omega A\right)^{2}}{2}}\sin ^{2}\left(\omega t+\phi \right)$ 總能量： $E=T+U$
阻尼諧振子能源		$E={\frac {m\left(\omega A\right)^{2}}{2}}e^{-bt/m}$

參考資料

Mayer, Sussman & Wisdom 2001，第xiii頁
Berkshire & Kibble 2004，第1頁
Berkshire & Kibble 2004，第2頁
Arnold 1989，第v頁
.
R.P. Feynman; R.B. Leighton; M. Sands. . Addison-Wesley. 1964: 31–7. ISBN 978-0-201-02117-2.
"Relativity, J.R. Forshaw 2009"
"Mechanics, D. Kleppner 2010"
"Relativity, J.R. Forshaw 2009"
"Relativity, J.R. Forshaw 2009"

Arnold, Vladimir I., 2nd, Springer, 1989, ISBN 978-0-387-96890-2
Berkshire, Frank H.; Kibble, T. W. B., 5th, Imperial College Press, 2004, ISBN 978-1-86094-435-2
Mayer, Meinhard E.; Sussman, Gerard J.; Wisdom, Jack, , MIT Press, 2001, ISBN 978-0-262-19455-6

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Mayer, Sussman & Wisdom 2001，第xiii頁

[2] Berkshire & Kibble 2004，第1頁

[3] Berkshire & Kibble 2004，第2頁

[4] Arnold 1989，第v頁

[5] .

[6] R.P. Feynman; R.B. Leighton; M. Sands. . Addison-Wesley. 1964: 31–7. ISBN 978-0-201-02117-2.

[7] "Relativity, J.R. Forshaw 2009"

[8] "Mechanics, D. Kleppner 2010"

[9] "Relativity, J.R. Forshaw 2009"

[10] "Relativity, J.R. Forshaw 2009"