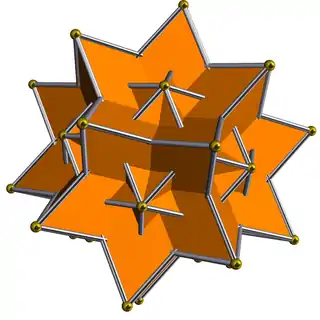
菱形六十面體
在幾何學中,菱形六十面體是一種星形菱形三十面體,由赫爾穆特·溫克爾巴赫(Helmut Unkelbach)於1940年發現[1],因此又稱為溫克爾巴赫六十面體(Unkelbach's hexecontahedron)[2]。這個星形多面體由60個黃金菱形以非凸的方式依照二十面體對稱性構成,共有60個面、120條稜和62個頂點。[3]此外,Al6Li3Cu之準晶體聚集體的核在緩慢結晶的情況下會形成菱形六十面體的形狀[4]。
 | ||
| 類別 | 星形菱形三十面體 | |
|---|---|---|
| 性質 | ||
| 面 | 60 | |
| 邊 | 120 | |
| 頂點 | 62 | |
| 歐拉特徵數 | F=60, E=120, V=62 (χ=2) | |
| 組成與佈局 | ||
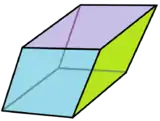
| 面的種類 |  黃金菱形 | |
| 對稱性 | ||
| 對稱群 | Ih, [5,3], (*532) | |
| 旋轉對稱群 | Ih, [5,3], (*532) | |
| 特性 | ||
| 環帶 | ||
| 圖像 | ||
| ||
歷史
菱形六十面體這種幾何結構最早由赫爾穆特·溫克爾巴赫(Helmut Unkelbach)於1940年發現,並做出了觀察及描繪。然而關於與這種形狀相似的分析與討論可能早在1619年就已經出現了[5]。1619年克普勒在其撰寫的書Harmonies of the World中對菱形三十面體進行了分析與討論[6][7],其中探討到了部分變體與菱形六十面體類似[5]。1984年D. Shechtman等人發現了一種五重對稱性的準晶體結構 [8],被認為與菱形六十面體十分接近[9][10],1986年這項發現被Guyot發表在《自然》上[4]。
性質
在不考慮面自相交的情況下,這種立體是一種六十面體[11],共有60個面、120條稜和62個頂點。[3]。然而若作為菱形三十面體的星形化體,則其是由30個自相交的多邊形構成。這種結構可以透過直接將菱形三十面體的面延伸來構成,如動畫所示。[3]
 菱形六十面體的面 |
 作為菱形三十面體的星形化體時的面。其中虛線以及淺色的部分為隱沒於立體的部分。 |
流行文化
| 外部圖片 | |
|---|---|
菱形六十面體是Wolfram Alpha的标志上所呈現的形狀[lower-roman 1],在沃尔夫勒姆研究公司中被稱為「spikey」[lower-roman 2]。
在巴西的文化中,有一種有色織物和紙板製成的菱形六十面體狀手工藝品,稱為幸福之心(happiness stars,或稱giramundos,葡萄牙語world turners)。這種手工藝品一般由母親縫製並作為送給女兒的結婚禮物。直到20世紀上半葉,巴西農村學校仍在教授手工藝的技術。然而由於近年來都市化的關係,這種習俗與工藝逐漸失傳[12]。
參考文獻
- Unkelbach, Helmut. . Deutsche Math. 1940, 5: 306–316.
- Branko Grünbaum. (PDF). lib.washington.edu. [2020-08-20]. (原始内容存档 (PDF)于2016-03-04).
- Kabai, Sándor. . Püspökladány, Hungary: Uniconstant. 2002: pp. 171, 179, 181.
- Guyot, P. . Nature (Nature Publishing Group). 1987, 326 (6114): pp.640–641.
- Kabai, Sándor,. (PDF). Proceedings of Bridges 2011. 2011: 387––394 [2020-08-20]. (原始内容存档 (PDF)于2020-08-24).
- Johannes Kepler. . Linz. 1619.
- George W. Hart. . Virtual Polyhedra. 1996 [2020-08-20]. (原始内容存档于2019-12-30).
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J. . Physical Review Letters. 1984, 53 (20): 1951–1953. Bibcode:1984PhRvL..53.1951S. doi:10.1103/PhysRevLett.53.1951.
- Á. Csanády, V. Stefániay, A. Griger, L. Tomcsányi, B. Albert,. . Proceedings of the 8th ILMC. 1987, 22/23 (6): 486.
- H.-U. Nissen, R. Wessicken, C. Beeli, Á. Csanády. . Philosophical Magazine B (Taylor & Francis). 1988, 57 (5): 587. doi:10.1080/13642818808211230.
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- [Handicraft-anticipated discovery of polyhedra], IMPA, [2019-01-08], (原始内容存档于2019-01-09) (葡萄牙语)
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- 一手資料