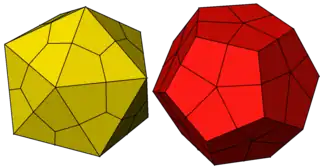
鳶形六十面體
在幾何學中,鳶形六十面體是一種卡塔蘭立體,由60個全等的箏形組成,是小斜方截半二十面体的對偶多面體,其拓樸結構與菱形六十面體相同[1],是6個不存在哈密頓路徑的卡塔蘭立體之一。[2]在圖論中,鳶形六十面體與菱形六十面體皆對應到鳶形六十面體圖,也就是說鳶形六十面體與菱形六十面體與拓樸同構[3]。
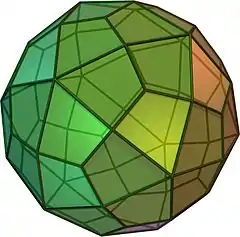 (按這裡觀看旋轉模型) | ||||
| 類別 | 卡塔蘭立體 六十面體 | |||
|---|---|---|---|---|
| 對偶多面體 | 小斜方截半二十面体 | |||
| 識別 | ||||
| 鮑爾斯縮寫 | sladit | |||
| 數學表示法 | ||||
| 考克斯特符號 | ||||
| 康威表示法 | oD 或 deD | |||
| 性質 | ||||
| 面 | 60 | |||
| 邊 | 120 | |||
| 頂點 | 62 | |||
| 歐拉特徵數 | F=60, E=120, V=62 (χ=2) | |||
| 二面角 | 154° 7′ 17′′ arccos(-19-8√5/41) | |||
| 組成與佈局 | ||||
| 面的種類 |  鳶形 | |||
| 面的佈局 | V3.4.5.4 | |||
| 頂點的種類 | 20個3階頂點 30個4階頂點 12個5階頂點 | |||
| 對稱性 | ||||
| 對稱群 | Ih, H3, [5,3], (*532) | |||
| 旋轉對稱群 | I, [5,3]+, (532) | |||
| 圖像 | ||||
| ||||
性質
鳶形六十面體由60個面、120條邊和62個頂點組成。[4]其中,60個面都是全等的鳶形。在其62個頂點中,有20個頂點是3個鳶形的公共頂點、30個頂點是4個鳶形的公共頂點和12個頂點是5個鳶形的公共頂點[5],這三種頂點分別可以對應到其對偶多面體小斜方截半二十面體的三種面上[6] 。鳶形六十面體不存在哈密頓路徑[2],換句話說,即在鳶形六十面體中找不到一條沿著鳶形六十面體的邊,恰好通過每個頂點、且不重覆拜訪頂點的路徑[7]。
正交投影
鳶形六十面體有3種具對稱性的投影位置,分別位於其三種頂點上。其中最後兩種的對偶圖之對稱性對應於A2和H2的考克斯特平面[13]。
| 投影對稱性 | [2] | [2] | [2] | [2] | [6] | [10] |
|---|---|---|---|---|---|---|
| 圖像 |  |
 |
 |
 |
 |
 |
| 對偶圖像 |  |
 |
 |
 |
 |
 |
變體
鳶形六十面體可以透過在正二十面體或正十二面體的面中心加入頂點,並加入從新頂點到原始邊的新邊來構造,[14]因此鳶形六十面體在康威多面體表示法中可以用oI或oD來表示[15]。這種幾何變換存在一個能連續變化的自由度,因此可以產生許多變體。以從正二十面體構建的版本為例,三角形中心加入頂點連接到邊緣可以是垂直於邊緣或著不垂直於邊緣,這將產生兩種不同的鳶形六十面體變體。[14]
用途
由於鳶形六十面體每個面都是相同的鳶形[16],因此有時會被用於製作六十面的骰子[17][18]。此外,在化學中,分子Au42N20模型呈鳶形六十面體,並具有一定程度的穩定性。[19]
 鳶形六十面體的骰子
鳶形六十面體的骰子
參考文獻
- Dave Barber. . 2009-12-01 [2021-08-25]. (原始内容存档于2022-03-18).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Livio Zefiro. . Universita' di Genova. [2021-08-25]. (原始内容存档于2021-08-25).
- . dmccooey.com. [2021-08-25]. (原始内容存档于2022-02-14).
- Koca, Mehmet and Ozdes Koca, Nazife and Koç, Ramazan. . Journal of Mathematical Physics (American Institute of Physics). 2010, 51 (4): 043501.
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- . fillygons.ch. [2021-08-29]. (原始内容存档于2022-03-31).
- Wolfram, Stephen. . from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- Wolfram, Stephen. . from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- Wolfram, Stephen. . from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- Wolfram, Stephen. . from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- Koca, Mehmet and Al-Ajmi, Mudhahir and Koç, Ramazan. . Journal of Mathematical Physics (American Institute of Physics). 2007, 48 (11): 113514.
- Piedade, Claudio Alexandre, (PDF), 2016 [2021-09-10], (原始内容存档 (PDF)于2021-09-10)
- Pieter Goetschalckx, (PDF), [2021-09-10], (原始内容存档 (PDF)于2021-09-10)
- Gábor Gévay. . WORLD SCIENTIFIC. 1992-03: 177–203 [2021-10-13]. ISBN 9789810206000. doi:10.1142/9789814439497_0012. (原始内容存档于2021-10-26) (英语).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- . chilloutkitchen.com. (原始内容存档于2021-07-28).
- Hong-Man Ma, Hui-Yan Zhao, Jing Wang, Ying Liu. . The Journal of Physical Chemistry C. 2020-01-09, 124 (1): 425–429 [2021-10-13]. ISSN 1932-7447. doi:10.1021/acs.jpcc.9b08443. (原始内容存档于2021-10-29) (英语).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.