表面能
表面能(英語:)是创造物质表面时,破坏分子间作用力所需消耗的能量。在固体物理理论中,表面原子比物质内部的原子具有更多的能量,因此,根据能量最低原理,原子会自发的趋于物质内部而不是表面。表面能的另一种定义是,材料表面相对于材料内部所多出的能量。把一个固体材料分解成小块需要破坏它内部的分子间作用力,所以需要消耗能量。如果这个分解的过程是可逆的,那么把材料分解成小块所需要的能量就和小块材料表面所增加的能量相等。但事实上,只有在真空中刚刚形成的表面才符合上述能量守恒。因为新形成的表面是非常不稳定的,它们通过表面原子重组和相互间的反应,或者对周围其他分子或原子的吸附,从而使表面能量降低。

表面能的测定
通过接触角测量来测量表面能
测量表面能的最常见方法是通过接触角实验。[1]在这种方法中,用几种液体(通常是水和二碘甲烷)测量表面的接触角。基于接触角的结果和已知道液体的表面张力,可以计算表面能。 实际上,这种分析是通过接触角仪自动完成的。[2]
有几种不同的模型可根据接触角读数计算表面能。[3]最常用的方法是OWRK,它需要使用两种探测液,并给出总的表面能并将其分为极性和分散成分。
接触角法是一种简单的表面能测量方法,因为它具有简便性,适用于各种表面以及快速的特性。测量可以完全自动化并且是标准化的。[4]
测量固体的表面能–其他方法
液体的表面能可以通过拉伸液体膜来测量(这增加了表面积并因此增加了表面能)。在那种情况下,为了使一定量的液体的表面积增加δA,需要功的量γ δA(其中,γ是液体的表面能密度)。但是,这样的方法不能用于测量固体的表面能,因为固体膜的拉伸除了增加表面能之外,还会在主体中诱发弹性能。
固体的表面能通常在高温下测量。在这样的温度下,固体潜变,即使表面积改变,体积也保持大致恒定。如果γ是半径为r和长度为l的圆柱棒在高温和恒定单轴张力P下的表面能密度,则在平衡时,总亥姆霍兹自由能的变分法消失,可以得到
其中F是亥姆霍兹自由能,A是棒的表面积:
而且,由于杆的体积(V)保持恒定,所以体积的变化(δV)为零,即:
因此,表面能密度可以表示为:
可以通过在平衡状态下测量P,r和l来计算固体的表面能密度。
该方法仅在固体是各向同性的情况下才有效,这意味着所有晶体学取向的表面能都相同。尽管这仅对非晶态固体(玻璃)和液体严格适用,但各向同性是许多其他材料的良好近似值。特别是,如果样品是多颗粒的(大多数金属)或通过粉末烧结制成的(大多数陶瓷),则这是一个很好的近似值。
在单晶材料(例如天然宝石)的情况下,表面能的各向异性会导致切面。晶体的形状(假设热力学平衡生长条件)与伍尔夫构型(Wulff construction)的表面能有关。因此,通过测量刻面的相对尺寸,可以发现刻面的表面能在比例常数内。
计算变形固体的表面能
在固体变形中,表面能可被视为“产生一个单位表面积所需的能量”,并且是变形前后系统总能量之差的函数:
- .
计算结晶固体的表面形成能
在密度泛函理论中,可以根据以下表达式计算表面能:
其中
- Eslab是使用密度泛函理论获得的表面平板的总能量。
- N是表面平板中的原子数。
- Ebulk是每个原子的总能量。
- A是表面积。
对于一个平板,有两个曲面,它们是同一类型,这在分母中用数字2来表示。为了保证这一点,需要仔细创建楼板,以确保上下表面的类型相同。
粘合接触的强度取决于粘合功,也称为两个接触体的相对表面能。[6]相对表面能可以通过将由一种材料制成的形状明确的物体与由第二材料制成的基板分离来确定。[7]例如,“有机玻璃-明胶”界面的相对表面能等于0.03 N / m。 在视频中可以看到用于测量相对表面能及其功能的实验装置。[8]
从升华热估算表面能
为了保证估算的准确,均匀材料的表面能,可以将材料的单个分子成分建模为立方体。需要能量将立方体从大部分材料中移动到表面。能源成本被纳入材料的表面能,可以通过以下方式量化:

其中zσ和zβ是与材料的表面和主体区域相对应的配位数,分别等于5和6; a0是单个分子的表面积,WAA是成对的分子间能。
可以通过对分子体积的立方根求平方来确定表面积:
此处,M̄对应于分子的摩尔质量,ρ对应于密度,NA是阿伏伽德罗数。
为了确定成对的分子间能量,必须破坏材料中的所有分子间力。这样可以更全面的研究单个分子发生的相互作用。在物质升华过程中,分子之间的分子间作用力被破坏,导致材料从固体变为气体。因此,在确定成对的分子间能时,考虑到升华焓是有用的。升华焓可以通过以下公式计算:
使用经验表式的升华焓值,可以确定成对的分子间能量。将该值结合到表面能方程中可以估算表面能。
下列方程式可以用作表面能的合理估计:
界面能
界面的存在通常会影响系统的所有热力学参数。有两种常用的模型来演示界面现象:Gibbs理想界面模型和Guggenheim模型。为了使用吉布斯模型演示界面系统的热力学,该系统可以分为三个部分:两种具有体积Vα和Vβ的不混溶的液体,以及一个无限薄的边界层,称为Gibbs划分平面(σ),将这两个体积分开。
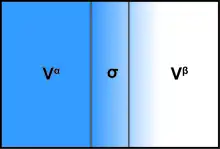
系统的总容量为:
系统的所有扩展量都可以写为三个组成部分的总和:体相α,体相β和界面σ。一些示例也包括内部能量U,第i个物质ni的分子数和熵S。
尽管这些量在每个组件之间可以变化,但是系统内的总和保持恒定。在界面上,这些值可能会与本体阶段中存在的值有所不同。界面处存在的分子浓度可以定义为:
其中ciα和ciβ分别代表物质i在本体相α和β中的浓度。

定义一个新的术语界面过量Γi是有益的,因此可以描述每单位面积的分子数量:
润湿性
传播参数
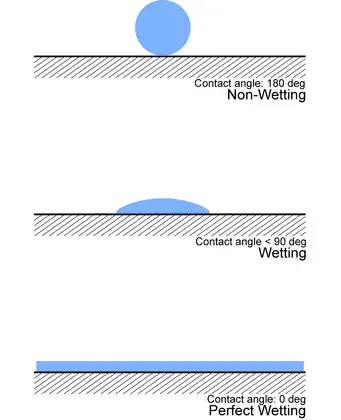
表面能在润湿现象中起作用。要对此进行检查,请考虑在固态基材上滴一滴液体。如果基材的表面能在添加液滴后发生变化,则称基材润湿。扩频参数可用于数学确定:
其中S是扩展参数,γs是基底的表面能,γl是液体的表面能,γs-l是基底和液体之间的界面能。
若S < 0,则液体会部分润湿基材。 若S > 0,则液体将基板完全润湿。[9]
表面能改性技术
最常用的表面改性方案是等离子体活化,湿化学处理(包括接枝)和薄膜涂层。[14][15][16]模拟表面能是一种使器件制造和包括图案化在内的表面修饰可以合并到使用单个器件材料的单个处理步骤中的技术。[17]
可以使用许多技术来增强润湿性。可以使用诸如电晕处理[18],等离子处理和酸蚀刻之类的表面处理[19]来增加基板的表面能。也可以将添加剂添加到液体中以降低其表面能。该技术通常用于油漆配方中,以确保将它们均匀地铺展在表面上。[20]
开尔文方程
由于液体固有的表面张力,形成弯曲的表面以最小化面积。这种现象是由形成表面的高能成本引起的。这种情况下,当曲面弯曲时,系统的吉布斯自由能被最小化。
开尔文方程式基于热力学原理,用于描述由曲面液体引起的蒸气压变化。蒸气压发生这种变化的原因是拉普拉斯压力。液滴的蒸气压高于平面的蒸气压,因为增加的拉普拉斯压力使分子更容易蒸发。相反,在气泡周围的液体中,相对于气泡内部的压力降低,从而使分子更难以蒸发。开尔文方程式表示为:
其中,PK
0是曲面的蒸气压,P0是平面的蒸气压,γ是表面张力,Vm是液体的摩尔体积,R是通用气体常数,T是温度(以开尔文为单位),R1和R2是表面曲率的主要半径。
涂料的表面改性颜料
颜料在改变涂料的应用性能方面具有巨大的潜力。由于其细粒度和固有的高表面能,其通常需要进行表面处理,以增强在液体介质中的分散性。以前已经使用了各种各样的表面处理方法,包括在存在极性基团的情况下分子表面上的吸附,聚合物的单层以及有机颜料表面上的无机氧化物层。[21]
随着较大的颜料颗粒分解成较小的子颗粒,新表面不断产生。因此,这些新形成的表面会产生更大的表面能,从而使生成的颗粒经常粘在一起形成聚集体。由于分散在液体介质中的颗粒处于恒定的热运动或布朗运动中,因此当其在介质中移动并发生碰撞时,其对附近的其他颜料颗粒具有很强的亲和力。[21]这种自然吸引力主要归功于强大的短程范德华力,这是其表面能的作用。
颜料分散的主要目的是分解聚集体并形成最佳尺寸颜料颗粒的稳定分散体。该过程通常涉及三个不同的阶段:润湿,分解和稳定。当配制要求良好的粘附性和外观的涂料时,易于润湿的表面是理想的。这也使与表面张力有关的缺陷(例如爬行,起皱和橘皮)的风险最小化。[22]这是颜料分散体的基本要求。 为了使润湿有效,颜料载体的表面张力必须低于颜料的表面自由能。[21]这使载体渗入颜料聚集体的空隙中,从而确保完全润湿。最后,使颗粒受到排斥力,以使它们彼此分离并降低絮凝的可能性。
分散体可能通过两种不同的现象变得稳定:电荷排斥和空间或熵排斥。[22]在电荷排斥中,具有相同电荷的粒子彼此排斥。或者,当分散体中的颜料颗粒的表面上存在被吸附的材料层(例如被溶剂溶胀的聚合物分子)时,位阻排斥或熵排斥是用来描述排斥作用的现象。仅聚合物分子的某些部分(锚)被吸附,它们相应的环和尾部延伸到溶液中。当颗粒彼此接近时,其的吸附层变得拥挤。 这提供了有效的空间屏障,可防止絮凝。[23]这种拥挤效应伴随着熵的降低,由此减少了在吸附层中聚合物分子可能的构象数目。结果,能量增加并且经常产生排斥力,该排斥力有助于使颗粒彼此分离。

常用表面能值表
| 材料 | 方向 | 表面能(mJ/m2) |
|---|---|---|
| 聚四氟乙烯(PTFE) | 19[24] | |
| 玻璃 | 83.4[25] | |
| 石膏 | 370[26] | |
| 铜 | 1650[27] | |
| 氧化镁 | (100) 水平 | 1200[28] |
| 氟化钙 | (111) 水平 | 450[28] |
| 氟化锂 | (100) 水平 | 340[28] |
| 碳酸钙 | (1010) 水平 | 23[28] |
| 氯化钠 | (100) 水平 | 300[29] |
| 氯化钠 | (110) 水平 | 400[30] |
| 氯化钾 | (100) 水平 | 110[29] |
| 氟化钡 | (111) 水平 | 280[28] |
| 硅 | (111) 水平 | 1240[28] |
參考資料
- Marshall, S. J.; Bayne, S. C.; Baier, R.; Tomsia, A. P.; Marshall, G. W. . Dental Materials. 2010, 26 (2): e11–e16. PMID 20018362. doi:10.1016/j.dental.2009.11.157 (英语).
- Laurén, S. . blog.biolinscientific.com. Biolin Scientific. [2019-12-31]. (原始内容存档于2019-12-31) (英语).
- . biolinscientific.com. Biolin Scientific. [2019-12-31]. (原始内容存档于2021-05-04) (英语).
- . ISO. 2017 [2021-05-02]. (原始内容存档于2021-05-02).
- Woodruff, D. P. (编). 10. Elsevier. 2002.
- . Springer. 2017. ISBN 9783662530801.
- Popov, V. L.; Pohrt, R.; Li, Q. . Friction. September 2017, 5 (3): 308–325. doi:10.1007/s40544-017-0177-3 (英语).
- Dept. of System Dynamics and Friction Physics. . December 6, 2017 [2018-01-28]. (原始内容存档于2021-05-07).
- Bonn, D.; Eggers, J.; Indekeu, J.; Meunier, J.; Rolley, E. . Reviews of Modern Physics. 2009, 81 (2): 739–805 [2021-05-13]. Bibcode:2009RvMP...81..739B. doi:10.1103/revmodphys.81.739. (原始内容存档于2021-05-13).
- Zisman, W. . Advances in Chemistry Series. Advances in Chemistry. 1964, 43: 1–51. ISBN 0-8412-0044-0. doi:10.1021/ba-1964-0043.ch001.
- Owens, D. K.; Wendt, R. C. . Journal of Applied Polymer Science. 1969, 13 (8): 1741–1747. doi:10.1002/app.1969.070130815.
- De Gennes, P. G. . Reviews of Modern Physics. 1985, 57 (3): 827–863. Bibcode:1985RvMP...57..827D. doi:10.1103/revmodphys.57.827.
- Kern, K.; David, R.; Palmer, R. L.; Cosma, G. . Physical Review Letters. 1986, 56 (26): 2823–2826. Bibcode:1986PhRvL..56.2823K. PMID 10033104. doi:10.1103/physrevlett.56.2823.
- Becker, H.; Gärtner, C. . Analytical and Bioanalytical Chemistry. 2007, 390 (1): 89–111. PMID 17989961. doi:10.1007/s00216-007-1692-2.
- Mansky. . Science. 1997, 275 (5305): 1458–1460. doi:10.1126/science.275.5305.1458.
- Rastogi. . ACS Nano. 2010, 4 (2): 771–780. PMID 20121228. doi:10.1021/nn901344u.
- Pardon, G.; Haraldsson, T.; van der Wijngaart, W. . Advanced Materials Interfaces. 2016, 3 (17): 1600404. doi:10.1002/admi.201600404.
- Sakata, I.; Morita, M.; Tsuruta, N.; Morita, K. . Journal of Applied Polymer Science. 2003, 49 (7): 1251–1258. doi:10.1002/app.1993.070490714.
- Rosales, J. I.; Marshall, G. W.; Marshall, S. J.; Wantanabe, L. G.; Toledano, M.; Cabrerizo, M. A.; Osorio, R. . Journal of Dental Research. 1999, 78 (9): 1554–1559. PMID 10512390. doi:10.1177/00220345990780091001.
- Khan, H.; Fell, J. T.; Macleod, G. S. . International Journal of Pharmaceutics. 2001, 227 (1–2): 113–119. PMID 11564545. doi:10.1016/s0378-5173(01)00789-x.
- Wicks, Z. W. 3rd. New York: Wiley Interscience. 2007: 435–441.
- Tracton, A. A. 3rd. Florida: Taylor and Francis Group. 2006: 31–6 – 31–7.
- Auschra, C.; Eckstein, E.; Muhlebach, A.; Zink, M.; Rime, F. . Progress in Organic Coatings. 2002, 45 (2–3): 83–93. doi:10.1016/s0300-9440(02)00048-6.
- Kinloch, A. J. . London: Chapman & Hall. 1987.
- Rhee, S.-K. . Journal of Materials Science. 1977, 12 (4): 823–824. Bibcode:1977JMatS..12..823R. S2CID 136812418. doi:10.1007/BF00548176.
- Dundon, M. L.; Mack, E. . Journal of the American Chemical Society. 1923, 45 (11): 2479–2485. doi:10.1021/ja01664a001.
- Udin, H. . JOM. 1951, 3 (1): 63. Bibcode:1951JOM.....3a..63U. doi:10.1007/BF03398958
 .
. - Gilman, J. J. . Journal of Applied Physics. 1960, 31 (12): 2208. Bibcode:1960JAP....31.2208G. doi:10.1063/1.1735524.
- Butt, H.-J.; Graf, Kh.; Kappl, M. . Weinheim: Wiley-VCH. 2006.
- Lipsett, S. G.; Johnson, F. M. G.; Maass, O. . Journal of the American Chemical Society. 1927, 49 (4): 925. doi:10.1021/ja01403a005.
参阅
- 接触角
- 表面张力系数
- 座滴法
- 毛细面
