錢德拉塞卡極限
錢德拉塞卡極限(),以印度裔美籍天文物理學家蘇布拉馬尼揚·錢德拉塞卡命名,是無自轉恆星以電子簡併壓力阻擋重力塌縮所能承受的最大質量,這個值大約是1.44倍太陽質量 [1][2],計算的結果會依據原子核的結構和溫度而有些差異[3]。錢德拉塞卡[4], eq. (36),[5], eq. (58),[6], eq. (43) 给出
此處, μe是分子的每電子平均質量,是氫原子的質量,而是與莱恩-埃姆登方程有關的常數,在數值上,這個值大約是 (2/μe)2 · 2.85 · 1030 公斤,或是,此處的是標準的太陽質量 [7],而是普朗克質量, ,是M的數量級極限MPl3/mH2。
對白矮星而言,電子簡併壓力是其抵抗重力的唯一力量,因此這個值也是白矮星的質量上限。主序星的質量若超過8倍的太陽質量,在演化結束前不能拋掉足夠的質量成為穩定的白矮星,因此會成為中子星或是黑洞 [8][9][10]。
物理學
電子簡併壓力是依據量子力學的所產生的效應。因為電子是費米子,在一個原子內不能有兩個電子有著相同的量子狀態,所以不可能讓所有的電子都在最低的能量。換言之,電子必然會佔有不同的能階。當原子被壓縮時,由於電子的數量和必須佔有不同的能階,所以必然會佔有一定量的體積。因此電子的能量將因為壓縮而增加,電子也必須施加壓力來抗拒電子雲的進一步壓縮。這就是電子簡併壓力的起源。
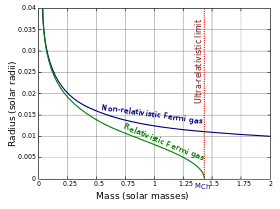
在非相對論的情況下,電子簡併壓力可以由狀態方程求得,形式為P=K1ρ5/3。解白矮星多方模型的流體靜力學等效方程式可以導出係數為3/2的半徑反比於質量的立方,和體積反比於質量的關係。[11] 當白矮星模型的質量增加時,電子簡併壓力使得特有的電子能量相對於它們的靜止質量不再是微不足道的。電子的速度接近光速,因此必須考慮到狹義相對論。在強大的相對論效應下,我們發現狀態方程的形式為P=K2ρ4/3。這將使多方模型的係數成為3,這會使總質量Mlimit只與K2相關聯。[12]
參考資料
- p. 55, How A Supernova Explodes, Hans A. Bethe and Gerald Brown, pp. 51–62 in Formation And Evolution of Black Holes in the Galaxy: Selected Papers with Commentary, Hans Albrecht Bethe, Gerald Edward Brown, and Chang-Hwan Lee, River Edge, NJ: World Scientific: 2003. ISBN 981238250X.
- Mazzali, P. A.; K. Röpke, F. K.; Benetti, S.; Hillebrandt, W. . Science. 2007, 315 (5813): 825–828. doi:10.1126/science.1136259.
- The Neutron Star and Black Hole Initial Mass Function (页面存档备份,存于), F. X. Timmes, S. E. Woosley, and Thomas A. Weaver, Astrophysical Journal 457 (February 1, 1996), pp. 834–843.
- The Highly Collapsed Configurations of a Stellar Mass (页面存档备份,存于), S. Chandrasekhar, Monthly Notices of the Royal Astronomical Society 91 (1931), 456–466.
- The Highly Collapsed Configurations of a Stellar Mass (second paper) (页面存档备份,存于), S. Chandrasekhar, Monthly Notices of the Royal Astronomical Society, 95 (1935), pp. 207--225.
- On Stars, Their Evolution and Their Stability (页面存档备份,存于), Nobel Prize lecture, Subrahmanyan Chandrasekhar, December 8, 1983.
- Standards for Astronomical Catalogues, Version 2.0 (页面存档备份,存于), section 3.2.2, web page, accessed 12-I-2007.
- White dwarfs in open clusters. VIII. NGC 2516: a test for the mass-radius and initial-final mass relations (页面存档备份,存于), D. Koester and D. Reimers, Astronomy and Astrophysics 313 (1996), pp. 810–814.
- An Empirical Initial-Final Mass Relation from Hot, Massive White Dwarfs in NGC 2168 (M35) (页面存档备份,存于), Kurtis A. Williams, M. Bolte, and Detlev Koester, Astrophysical Journal 615, #1 (2004), pp. L49–L52; also arXiv astro-ph/0409447 (页面存档备份,存于).
- How Massive Single Stars End Their Life (页面存档备份,存于), A. Heger, C. L. Fryer, S. E. Woosley, N. Langer, and D. H. Hartmann, Astrophysical Journal 591, #1 (2003), pp. 288–300.
- The Density of White Dwarf Stars, S. Chandrasekhar, Philosophical Magazine (7th series) 11 (1931), pp. 592–596.
- The Maximum Mass of Ideal White Dwarfs (页面存档备份,存于), S. Chandrasekhar, Astrophysical Journal 74 (1931), pp. 81–82.
延伸讀物
- On Stars, Their Evolution and Their Stability (页面存档备份,存于), Nobel Prize lecture, Subrahmanyan Chandrasekhar, December 8, 1983.
- White dwarf stars and the Chandrasekhar limit (页面存档备份,存于), Masters' thesis, Dave Gentile, 帝博大學, 1995.
- Estimating Stellar Parameters from Energy Equipartition(页面存档备份,存于), sciencebits.com. Discusses how to find mass-radius relations and mass limits for white dwarfs using simple energy arguments.
相關條目
- 簡併物質
- 托爾曼-奧本海默-沃爾科夫方程
- 馬克士威-玻茲曼統計