黏着空间
在数学中,黏着空间()是拓扑学中一个常见构造,它将一个拓扑空间贴或“黏合”到另一个。 具体地,设 X 与 Y 是一个拓扑空间以及 Y 的一个子空间A。设 f : A → X 是一个连续映射(称为贴映射,)。黏着空间 X ∪f Y 之构造如下:先取 X 与 Y 的不交并然后对所有属于 A的 x ,将 x 与 f(x) 等化。用数学符号表示为:
有时黏着空间也写成 。在直觉上,我们认为 Y 通过映射 f 黏合到 X。
作为一个集合,X ∪f Y 由 X 与 (Y − A) 的不交并组成;但其拓扑由商构造确定。当 A 是 Y 的一个闭子集时,可以证明映射 X → X ∪f Y 时一个闭嵌入且 (Y − A) → X ∪f Y 是一个开嵌入。
例子
范畴描述
黏着构造是拓扑空间范畴中推出的例子。这就是说,黏着空间是关于如下交换图表的泛对象:
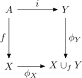
这里 i 是包含映射而 φX, φY 是分别商映射与到X 和 Y 不交并的典范单射的复合。可以将 i 换成任意一个连续映射 g 构造一个一般的推出——过程是类似的。反之,如果 f 也是一个包含黏着构造不过是将 X 与 Y 沿着它们的公共子空间简单的黏合。
参考文献
- Stephen Willard, General Topology, (1970) Addison-Wesley Publishing Company, Reading Massachusetts. (提供了一个简明的介绍。)
- . PlanetMath.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.