2019年國際單位制基本單位重新定義

國際單位制基本單位的新定義於2019年5月20日《米制公約》144週年紀念之日生效。[1][2]根據新定義，公斤、安培、開爾文及摩爾四個基本單位改為以固定物理常數的精確值的方式定義，這些常數分別為普朗克常數（ $h$ ）、基本電荷（ $e$ ）、波茲曼常數（ $k B$ ）及亞佛加厥常數（ $N A$ ）；秒、米和坎德拉此前已經以固定物理常數值的方式定義，它們的新定義在舊定義的基礎上作了修正。這些定義上的改變都以不變動基本單位的數值為前提，如此確保之前的各種測量數值可以繼續使用，不受影響。[3][4]在過去幾十年內，科學家致力於研發精確測量物理常數的實驗方法，直到2018年，國際計量委員會（CIPM）終於認為實驗條件成熟，向國際計量大會提交了修改國際單位制定義的提案。[5]^:23提案在2018年11月第26屆國際計量大會（CGPM）上一致通過。[6][7]

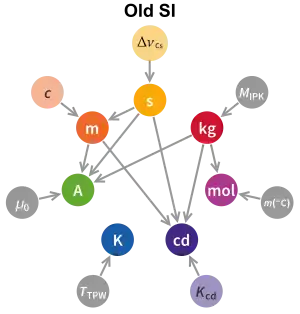
重新定義後的國際單位制：基本單位的定義僅依賴於固定數值的物理常數以及其他基本單位。

1983年後、2019年前的國際單位制：基本單位的定義不但依賴其他基本單位和物理常數（例如，米是由光在若干秒期間走過的路程定義的），而且還依賴於人造物件（如國際公斤原器）

此前，公制曾在1960年大幅改動，國際單位制（SI）正式面世。米的定義曾歷經根本性的變更：其原先定義為國際米原器的長度，後改為氪-86某特定譜線的波長的倍數。[註 1]此後，米的定義可以從測量自然現象而得，不再依賴於個人造物件。然而，公斤仍然定義為國際公斤原器的質量，是當時國際單位制中唯一仍受人造物件定義的單位。當時，國際單位制以七個基本單位為基礎，它們的十進制冪則用於定義其他所有單位。2019年的新單位制則以七個物理常數為基礎，所有單位都能從這些物理常數直接定義。「基本單位」不再是一個必需的概念，但在新單位制中予以保留。[4]

公制是國際單位制的前身，其設計初衷是，所有單位都應能從不變的自然現象中推導而得，[8]但由於現實測量技術上的局限性，單位的實際定義只能依賴於人造物件。1799年公制在法國面世時，科學家分別製造了國際米原器和國際公斤原器作定義之用。儘管這兩件原器的設計均以長期穩定不變為原則，這些原器及其複製品之間還是隨時間出現了細微的質量差異。科學進步必將超越這些原器所能提供的準確度，因此尋找新的定義取代它們成為了當務之急。另外，雖然一些單位是以自然現象定義，但這些現象不容易準確測量（如水的三相點曾用於定義開爾文）。2019年的新定義對這類單位做了改動，並淘汰了人造原器，自此所有單位都以可以準確測量的物理常數來定義。

背景

在1791年至1960年間，國際單位制的基本結構經歷了約170年的發展。1960年以後，隨著科技的日益進步，國際單位制的諸多缺陷也得到了一步步解決。

國際單位制的發展

法國革命早期，國民制憲議會的幾位領袖決定設立一套以邏輯和自然現象為基礎的新計量系統。米被定義為從北極至赤道距離的一千萬分之一，公斤則被定義為一立方米純水質量的千分之一。雖然這些定義意味著這些單位不再受強權一手掌握，但它們測量不易，使用不便。在現實使用上，分別以米原器（法語：）和公斤原器（法語：）作為這些單位的定義標準。[9]

到1875年，歐洲和拉丁美洲社會已廣泛使用公制，二十個工業發達國家簽署《米制公約》，設立了三個國際組織，負責保管國際米原器和國際公斤原器，並監督各國原器的比對和校準。[10][11]這三個國際組織分別為：

國際計量大會（法語：）：每四至六年舉辦一次，由各成員國代表組成，目的是討論與國際單位制推廣和改進有關的各項安排，以及對新的計量學測量數值進行審核。
國際計量委員會（法語：）：由十八名國際計量大會選出、來自不同國家的科學家組成，每年在國際度量衡局召開會議，並對國際度量衡大會提出行政上和技術上的建議。國際計量委員會以下有若干附屬委員會，其中的單位顧問委員會負責向國際計量委員會提供和計量單位有關的建議。[12]
國際計量局（法語：）：負責保管國際公斤原器，並定期將各國的米和公斤原器與國際公斤原器進行比較。國際計量局是國際計量大會和國際計量委員會的秘書處。

1889年第一屆國際計量大會正式採納40個米原器和40個公斤原器作為《米制公約》所規定的定義基準，原器均由英國莊信萬豐公司製造。[13]國際計量大會隨機選出各一個作為國際原器，再保留幾個作為複製品，其餘的則分配到各個成員國作為國家原器。每隔40年左右，各國的原器須與國際原器校對。[14]

《米制公約》在1921年修訂，規定國際計量大會除質量和長度外，亦須為其他計量單位設立標準定義。國際計量大會在1946年訂立了電流、光度的標準定義，後來再於1948年、1956年和1971年分別訂立了溫度、時間和摩爾質量的標準。[15]1948年第九屆國際計量大會委派國際計量委員會為一種單一整合、能供遵守《米制公約》的世界各國使用的單位制提出建議。[16]國際計量委員會在1960年第11屆大會上提交了這份建議書，大會正式通過議案，並將新的統一計量系統稱為國際單位制（法語：，簡稱SI）。[17]

重新定義的必要性

在2019年之前，國際單位制曾經經歷過多次重新定義。1960年第11屆國際計量大會將米重新定義為氪-86某一特定譜線波長的倍數，並淘汰先前的米原器。1967年第13屆大會將秒重新定義為銫-133原子在基態下的兩個超精細能級之間躍遷所對應的輻射波動週期的倍數，取代原先基於地球自轉週期的定義。[18]1983年第17屆國際計量大會又再次重新定義米：先固定光速在米每秒單位下的準確數值，然後利用秒來定義米。[19]

K21至K40國家原器以及國際公斤原器兩個複製品K32和K8(41)的質量變化。[註 2]所有質量變化都是相對於國際公斤原器。[20]

各個公斤原器從製成至今，質量都已有所變化。以國際公斤原器為準，它們每年的質量改變幅度在6992200000000000000♠2×10⁻⁸公斤以下。沒有任何方法能判斷，究竟是這些複製品的質量有所提高，還是國際公斤原器本身質量有所降低。[21]質量漂移的可能原因包括，原器吸收了汞蒸汽，或受到了碳化合物的污染。[22][23]在1999年第21屆國際計量大會上，專家敦促各國研究出一種不以某件實物為基準的公斤定義方法。計量學家一共提出了多種依賴基礎物理常數的定義方法，其中的亞佛加厥計劃和基布爾秤（在2016年之前稱為瓦特秤）都能夠間接但精確地測重。[24]

2007年，測溫法顧問委員會向國際計量委員會提交了一份研究報告。報告指出，當時的開爾文定義並不能有效適用於7001200000000000000♠20 K以下或7003130000000000000♠1300 K以上的溫度。報告認為波茲曼常數比三相點更適合作為測溫的基礎，因為前者在更大的溫度範圍內仍然適用。[25]

2007年第23屆國際計量大會上，大會要求國際計量委員會研究如何利用物理常數來定義所有的計量單位，從而淘汰當時所用的人造原器。國際純粹與應用物理學聯合會（IUPAP）在翌年表示支持這一建議。[26]2010年9月，單位顧問委員會在英國雷丁召開會議，原則上通過了《國際單位制手冊》的修訂草案。[27][28]單位顧問委員會在同年10月向國際計量委員會提交草案，但後者認為，第23屆大會所定下的條件還沒有被滿足，[註 3]所以暫時不建議對國際單位制做任何修訂。[30]在一年後召開的第24屆大會上，國際計量委員會提出決議，從原則上同意國際單位制的新定義，但新定義仍有待具體細節落實後才可生效。[31]大會通過了此項決議，[32]第25屆大會也從2015年提早至2014年召開。[33][34]2014年11月20日第25屆大會上，專家承認在必要條件上有所進展，但條件並未完全達到，因此這屆會議不會通過國際單位制的修訂議案。[35]直到2017年，各常數測量方法的精確度終於能夠滿足大會定下的條件，[36]國際單位制的修訂議案因此在2018年11月13至16日的第26屆國際計量大會上成功通過。

新定義

1983年，米的定義改為以固定光速的準確數值為基礎推算而得。建立在這一原則上，單位顧問委員會和國際計量局提倡固定以下四個常數的準確數值，從而得出基本單位的定義：

普朗克常數（ $h$ ）固定為6966662607015000000♠6.62607015×10⁻³⁴焦耳·秒（J⋅s）；
基本電荷（ $e$ ）固定為6981160217663400000♠1.602176634×10⁻¹⁹庫侖（C）；
波茲曼常數（ $k$ ）固定為6977138064900000000♠1.380649×10⁻²³焦耳每開爾文（J⋅K⁻¹）；
亞佛加厥常數（ $N A$ ）固定為7023602214076000000♠6.02214076×10²³個每摩爾（mol⁻¹）。

2006年版《國際單位制手冊》就已有描述這幾個常數，但在此版本中後三個常數被定義為「由實驗所得的常數」，而不是「定義所用的常數」。

以下常數的數值則應繼續保持不變：

光速（ $c$ ）固定為7008299792458000000♠299792458 米每秒（m⋅s⁻¹）；
銫-133原子在基態下的兩個超精細能級之間躍遷所對應的輻射頻率（ $Δ ν Cs$ ）固定為7009919263177000000♠9192631770 赫茲（Hz）；
頻率為7014540000000000000♠540×10¹² Hz的單色輻射的發光效率（ $K cd$ ）固定為7002683000000000000♠683 流明每瓦特（lm⋅W⁻¹）。

根據第9版《國際單位制手冊》，將以上七項定義中的導出單位（焦耳、庫侖、赫茲、流明及瓦特）以基本單位（秒、米、公斤、安培、開爾文、摩爾、坎德拉）重新表示，如下。[4]以下sr表示球面度，是一個無因次單位。

$Δ ν Cs$ = $Δ ν (133 Cs) hfs$ = 7009919263177000000♠9192631770 s⁻¹
$c$ = 7008299792458000000♠299792458 m⋅s⁻¹
$h$ = 6966662607015000000♠6.62607015×10⁻³⁴ kg⋅m²⋅s⁻¹
$e$ = 6981160217663400000♠1.602176634×10⁻¹⁹ A⋅s
$k$ = 6977138064900000000♠1.380649×10⁻²³ kg⋅m²⋅K⁻¹⋅s⁻²
$N A$ = 7023602214076000000♠6.02214076×10²³ mol⁻¹
$K cd$ = 7002683000000000000♠683 cd⋅sr⋅s³⋅kg⁻¹⋅m⁻²

在新定義下，國際公斤原器被正式淘汰。公斤、安培和開爾文的定義完全改變，摩爾的定義也有所修訂。這些改變會影響到基本單位的定義，但不會影響導出單位的表達形式。

對基本單位定義的影響

根據單位顧問委員會的提案，所有基本單位的定義都有所修改或重寫，定義的主要對象從基本單位轉移到物理常數的值。[38]以基本單位為定義對象，也就是取該單位的某個現實範例作為其定義標準，例如英格蘭國王愛德華二世在1324年把三顆大麥粒之長定義為一英吋，[39]以及自1889年起以國際公斤原器的質量作為一公斤的定義。相對之下，以物理常數的值作為定義對象，也就是先把一些自然界物理常數固定成某個特定的數值，再指定基本單位與這些常數之間的關係，例如在1983年，光速被固定為每秒7008299792458000000♠299792458米，由於已經有了秒的定義，所以一米的確切長度就可以推算得出。下文為每個基本單位分別列出2019年以前的定義[19]及2019年生效的新定義[4][37]。

秒

秒的定義沒有重大改變，只是其重點從單位本身轉移至物理常數的固定值。

舊定義：一秒等於銫-133原子在基態下的兩個超精細能級之間躍遷所對應的輻射的7009919263177000000♠9192631770個週期的時間。
2019年定義：秒，符號為s，國際單位制時間單位。其定義是，將銫-133原子不受擾動的基態超精細能級躍遷頻率 $Δ ν Cs$ 的值固定為7009919263177000000♠9192631770赫茲，赫茲等於s⁻¹。

秒和定義所用常數之關係如下：

1 s =

.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}7009919263177000000♠9192631770/ΔνCs

米

米的定義沒有重大改變，只是表達的語言更為嚴謹。

舊定義：光在1/7008299792458000000♠299792458秒內在真空中行進的距離。
2019年定義：米，符號為m，國際單位制長度單位。其定義是，將真空中的光速 $c$ 的值固定為每秒7008299792458000000♠299792458米，秒是以銫頻率 $Δ ν Cs$ 來定義的。

米和定義所用常數之關係如下：

1 m =

7009919263177000000♠ 9192631770 / 7008299792458000000♠ 299792458 c / Δ ν Cs

公斤

用國際公斤原器來測量普朗克常數的基布爾秤[40]

公斤的定義有根本性的改變。舊定義依賴於人造國際公斤原器，[41]新定義則是用普朗克常數得出某特定頻率的單個光子的能量，再用質能等價原理得出該光子能量所等同的質量。

舊定義：公斤是質量單位。一公斤等於國際公斤原器的質量。
2019年定義：公斤，符號為kg，國際單位制質量單位。其定義是，將普朗克常數 $h$ 的值固定為6966662607015000000♠6.62607015×10⁻³⁴ J⋅s，J·s等於kg⋅m²⋅s⁻¹，其中的米和秒是以 $c$ 和 $Δ ν Cs$ 來定義的。

以上的新定義還可以這樣等價地表達：一公斤等於和頻率總和為7050135639248965200♠1.356392489652×10⁵⁰赫茲的一組光子具有相同能量的物體的靜止質量。[42]

公斤和定義所用常數之關係如下：

1 kg =

(7008299792458000000♠ 299792458) 2 / (6966662607015000000♠ 6.626 07015 \times 10 -34)(7009919263177000000♠ 9192631770) h Δ ν Cs / c 2

一些推導單位和各常數之間的關係如下：

1 J⋅s =

h / 6966662607015000000♠ 6.626 07015 \times 10 -34

1 J =

h Δ ν Cs / (6966662607015000000♠ 6.626 07015 \times 10 -34)(7009919263177000000♠ 9192631770)

1 W =

h (Δ ν Cs) 2 / (6966662607015000000♠ 6.626 07015 \times 10 -34)(7009919263177000000♠ 9192631770) 2

1 N =

7008299792458000000♠ 299792458 / (6966662607015000000♠ 6.626 07015 \times 10 -34)(7009919263177000000♠ 9192631770) 2 h (Δ ν Cs) 2 / c

安培

安培的定義有根本性的改變。舊定義在現實中不容易應用，新定義則易明易用。

舊定義：在真空中相距一米的兩根橫截面為圓形、粗度可忽略不計的無限長平行直導線，各通上相等的恆定電流，當兩根導線之間每米長度所受力為6993200000000000000♠2×10⁻⁷牛頓時，各導線上的電流定義為一安培。
2019年定義：安培，符號為A，國際單位制電流單位。其定義是，將基本電荷 $e$ 的值定義為6981160217663400000♠1.602176634×10⁻¹⁹庫侖，庫侖等於A⋅s，其中的秒是以 $Δ ν Cs$ 定義的。

安培和定義所用常數之關係如下：

1 A =

e Δ ν Cs / (6981160217663400000♠ 1.602 176634 \times 10 -19)(7009919263177000000♠ 9192631770)

.

以上的新定義等同於把一庫侖定義為基本電荷的倍數：

1 C =

e / 6981160217663400000♠ 1.602 176634 \times 10 -19

舊定義提到了力的單位，而力的因次是MLT⁻²，因此必須先定義公斤、米和秒之後，才能定義安培。在舊定義下，真空磁導率（ $μ 0$ ）的準確值固定為6993400000000000000♠4π×10⁻⁷ H⋅m⁻¹。[43]由於光速（ $c$ ）的準確值也是固定的，所以根據以下公式

c^{2}={\frac {1}{\mu _{0}\varepsilon _{0}}}

，

Z_{0}={\sqrt {\frac {\mu _{0}}{\varepsilon _{0}}}}

真空電容率（ $ε 0$ ）和自由空間阻抗（ $Z 0$ ）都有固定的準確值。[44]

在新定義下，安培的定義不再提到公斤和米，但仍然依賴於秒的定義。另外，真空磁導率、真空電容率和自由空間阻抗的數值不再是固定的，而是會隨實驗改變，並帶有不確定度。[45]例如，真空磁導率的相對不確定度與精細結構常數 $α$ 相同。[46]根據CODATA 2018， $α$ 的標準相對不確定度為6990150000000000000♠1.5×10⁻¹⁰。

一些推導單位和各常數之間的關係如下：

1 V =

6981160217663400000♠ 1.602 176634 \times 10 -19 / (6966662607015000000♠ 6.626 07015 \times 10 -34)(7009919263177000000♠ 9192631770) h Δ ν Cs / e

1 Wb =

6981160217663400000♠ 1.602 176634 \times 10 -19 / 6966662607015000000♠ 6.626 07015 \times 10 -34 h / e

1 Ω =

(6981160217663400000♠ 1.602 176634 \times 10 -19) 2 / 6966662607015000000♠ 6.626 07015 \times 10 -34 h / e 2

開爾文

開爾文的定義有根本性的改變，不再用水的三相點，而是固定波茲曼常數的準確值。

舊定義：開爾文，熱力學溫度單位，等於水的三相點熱力學溫度的1/273.16。
2019年定義：開爾文，符號為K，國際單位制熱力學溫度單位。其定義是，將波茲曼常數的值 $k$ 固定為6977138064900000000♠1.380649×10⁻²³ J·K⁻¹，J·K⁻¹等於kg⋅m²⋅s⁻²⋅K⁻¹，其中的公斤、米和秒是以 $h$ 、 $c$ 和 $Δ ν Cs$ 定義的。

開爾文和定義所用常數之關係如下：

1 K =

6977138064900000000♠ 1.380 649 \times 10 -23 / (6966662607015000000♠ 6.626 07015 \times 10 -34)(7009919263177000000♠ 9192631770) h Δ ν Cs / k

摩爾

一個由超純矽製成的近乎完美球體，由亞佛加厥計劃製造，旨在準確測量亞佛加厥常數的值[40]

摩爾的舊定義依賴於公斤的定義，新定義則不再提到公斤，而是直接固定一摩爾物質所含的粒子數目。

舊定義：一摩爾物質所含的基礎單元數量相等於0.012公斤碳-12所含的原子數量。當使用摩爾時，必須指定基礎單元是原子、分子、離子、電子還是其他粒子或粒子集體。
2019年新定義：[5]^:22摩爾，符號為mol，國際單位制物質量單位。一摩爾所含的基礎單元數量等於7023602214076000000♠6.02214076×10²³個。此數字稱為亞佛加厥數，是亞佛加厥常數 $N A$ 以mol⁻¹單位表達時的固定值。[5][47]

摩爾和定義所用常數之關係如下：

1 mol =

7023602214076000000♠ 6.022 14076 \times 1023 / N A

.

新定義意味著，¹²C原子質量、原子質量單位（又稱道爾頓）、公斤及亞佛加厥常數之間的關係不再成立。以下兩句陳述之中，有一句必須改變：

一顆¹²C原子的質量等於12道爾頓；
與一道爾頓質量相同的克數等於亞佛加厥常數，即1 g/Da = 1 mol ⋅ $N A$ 。

根據第9版《國際單位制手冊》，第一句仍然成立，也就是第二句不再成立。[4][註 4]摩爾質量和相對原子質量之比（又稱摩爾質量常數）曾經是1 g/mol，但在新定義下不再是這個數值，但仍然極為相近。《國際單位制手冊》附錄2寫道：「碳-12的摩爾質量M(¹²C)等於6998120000000000000♠0.012 kg⋅mol⁻¹，其相對不確定度與 $N A h$ 的相對不確定度相同，在此決議通過時為6990450000000000000♠4.5×10⁻¹⁰。數值在未來將通過實驗測量而得。」[48][49]這句話沒有提到道爾頓，而且和以上兩句陳述都不矛盾。

坎德拉

坎德拉的定義沒有重大改變，只是它所依賴的公斤、米和秒有所改變。

舊定義：頻率為7014540000000000000♠5.4×10¹⁴ Hz的單色光源在特定方向輻射強度為1/683 W/sr時的發光強度。
2019年定義：坎德拉，符號為cd，國際單位制中某特定方向發光強度的單位。其定義是，將頻率為7014540000000000000♠540×10¹² Hz的單色輻射的發光效能 $K cd$ 固定為7002683000000000000♠683 lm⋅W⁻¹，lm⋅W⁻¹等於cd⋅sr⋅W⁻¹，即cd⋅sr⋅kg⁻¹⋅m⁻²⋅s³，其中的公斤、米和秒是以 $h$ 、 $c$ 和 $Δ ν Cs$ 定義的。

坎德拉和定義所用常數之關係如下：

1 cd =

1 / 683(6966662607015000000♠ 6.626 07015 \times 10 -34)(7009919263177000000♠ 9192631770) 2 K cd h (Δ ν Cs) 2 / sr

可重現度

國際單位制的七個基本單位均以固定數值的常數定義，其中六個為自然界物理常數，一個為表達個數的常數。[註 5][50]定義所用到的常數共有七個，但除了秒和摩爾以外，其他基本單位與常數之間並沒有一對一的關係，而是需要多個常數相互結合而得。

科學家在設計新國際單位制的時候，可選擇做定義標準的物理常數不止六個。例如，只要長度和時間單位確定後，萬有引力常數G從因次分析的角度來說也可以用做質量單位的定義標準。不過事實上G的測量不確定度約為10⁻⁵，[註 6]意味著公斤定義的最高可重現度約為10⁻⁵。相比之下，國際公斤原器質量的測量可重現度為1.2 × 10⁻⁸。[45]新定義選用物理常數的條件是，常數的測量不確定度必須很低，而且測量方法必須盡可能獨立於其他所用常數。在正式定義以外，國際計量局還研發了一套可供實現定義的實用方法，[51]但這些實用測量方法並不屬於正式定義的一部分。

採納過程

國際計量委員會的不少工作，都是由附屬其下的不同顧問委員會所負責。其中，單位顧問委員會負責提出單位重新定義的方案，其他顧問委員會則對方案提出建議。在接受單位顧問委員會的方案之前，必須先滿足以下條件：

在公斤的重新定義方面，須進行三個測量普朗克常數的不同實驗，每個實驗的95%相對不確定度均在6992500000000000000♠5×10⁻⁸以內，其中一個實驗須比6992200000000000000♠2×10⁻⁸更加準確。這些實驗須包括基布爾秤和亞佛加厥計劃，兩者結果必須一致。[52][53]
在開爾文的重新定義方面，分別用聲氣測溫法和介電常數氣體測溫法測量波茲曼常數，相對不確定度均在10⁻⁶以內，實驗結果須經其他實驗證實。[54]

2011年3月，國際亞佛加厥協調小組達到了6992300000000000000♠3.0×10⁻⁸的不確定度，而美國國家標準技術研究所則達到了6992360000000000000♠3.6×10⁻⁸的不確定度。[24]2012年9月1日，歐洲國家計量學研究所聯會正式啟動項目，目的是把基布爾秤和亞佛加厥計劃之間的相對差從6993170000000000000♠(17±5)×10⁻⁸降低至6992200000000000000♠2×10⁻⁸以內。[55]2013年3月，重新定義後的國際單位制被稱為「新SI」，[3]但有科學家認為，由於新制用到了原子尺度上的量子現象，因此應更準確地稱為「量子SI」。[56]

CODATA於2016年發佈了直至2014年底所測得的基本物理常數之建議值。所有測量皆符合國際計量大會的條件，重新定義的時機終於成熟，只待2018年末的下一屆國際計量大會。[57][58]2017年10月20日，國際計量委員會第106次會議正式採納了國際單位制修正草案，並呈交至第26屆國際計量大會投票決議。[5]^:17–23同日，[5]^:22CODATA基礎常數任務組發表了2017版常數測量值，不但列出了四個即將用於定義國際單位制的常數的不確定度，還列出了新制下他們所建議的固定精確值。[37]2018年11月16日，國際計量大會一致通過提案，國際單位制新定義於2019年5月20日正式生效。[59]

顧慮

2010年，澳洲聯邦科學與工業研究組織科學家馬庫斯·福斯特（Marcus Foster）發表了一篇評判國際單位制的論文。論文提到了國際單位制的一些基本問題，如Ω等符號輸入不便，單位制所用的計量學概念缺乏嚴謹的數學表述，等等。他還認為，新制所保留的坎德拉和摩爾並非真正的基本單位。[60]

以單位還是常數為定義對象

有科學家對以常數為對象的單位定義方法提出質疑，認為如果不以某個實例來直接定義單位，會有不理想的後果。[61]在新定義下，要得出一公斤質量，無法再直接測量國際公斤原器，而是必須先測量普朗克常數 $h$ ，然後運用狹義相對論和量子力學原理進行換算。[62]相反，安培的新定義卻比舊定義更接近於「某個實例」。[63]先前的定義提到帶電流的平行直導線之間的力，但量子尺度和經典宏觀尺度下的電磁相互作用並不相同，所以有科學家認為，用宏觀現象來定義在量子尺度上所用的計量單位，有失妥當。[45]

質量與亞佛加厥常數

自從科學家在2005年發現國際公斤原器和各個國家公斤原器之間出現了質量偏差，科學界就開始討論公斤應該如何定義的問題。脫穎而出的定義方法共有兩個。第一，通過固定亞佛加厥數，經亞佛加厥計劃測量單個矽-28原子的質量，從而直接定義公斤。第二，利用基布爾秤精確地測量普朗克常數，通過推算定義公斤。[64]有科學家批評，新單位制選擇了第二種定義方法，斷開了原先摩爾、公斤、道爾頓和亞佛加厥常數（ $N A$ ）之間的緊密關係。[註 7]另外有不少學者認為，摩爾並不是一個真正的計量單位，而只不過是個比例因子。[60][65]

第8版《國際單位制手冊》把道爾頓定義為單個¹²C原子的質量，[66]並以道爾頓和公斤來定義亞佛加厥常數。沿用新定義的第9版《手冊》[4]則固定亞佛加厥常數的值，並保留道爾頓的定義，但道爾頓和公斤之間的關係就必須斷開。[67][68]

1993年，國際純化學和應用化學聯合會（IUPAC）認可道爾頓為等同於原子質量單位的單位，[69]國際計量大會也接著在《國際單位制手冊》中收錄了道爾頓。[70]公斤和摩爾的新定義生效後，第9版《手冊》仍然將道爾頓視為和原子質量單位相等的單位，兩者皆等於單個碳-12原子質量的1/12，此定義完全獨立於公斤的定義。[4]美國艾克朗大學科學家布萊恩·倫納德（Brian Leonard）曾在2012年提出，道爾頓（Da）應該用以下公式定義： $N A$ = (g/Da) mol⁻¹，而原子質量單位（ $m u$ ）則應繼續等於碳-12原子質量，也就是道爾頓不再等同於原子質量單位，兩者的相對差約為10⁻¹⁰。[71]

溫度

不同溫度範圍須用到不同的測溫方法：室溫附近的溫度可以用溫度計中液體的熱脹冷縮測得，更高的溫度則往往通過黑體輻射的顏色推算。沃伊切赫·T·黑拉（Wojciech T. Chyla）在《波蘭物理學會期刊》上發表論文，從哲學的角度審視國際單位制的結構，認為溫度並不是一個真正的基本單位，而只是一組粒子的平均熱能。[45]論文指出，不少理論物理論文都將溫度（或其倒數）寫作 $Θ$ 或 $β$ ：

\Theta =kT;\ \ \ \beta ={1 \over kT}

，

其中 $k$ 是波茲曼常數。不過黑拉也承認，溫度在宏觀世界裡還是起到了基本單位的作用，是熱力學中不可或缺的概念。[45]

在測溫法顧問委員會於1990年所公佈的實用測溫方法中，要測出極低和極高的溫度，都須先測量其對應的能量，然後用波茲曼常數進行換算。[72][73]

發光強度

福斯特認為，以坎德拉（ $cd$ ）為單位的發光強度並不是一個物理量，而是光生物學中和人類視覺有關的量，因此坎德拉不應該被視為基本單位。[60]1979年，科學界轉為用光通量（ $Φ$ ）來定義各種光度學單位，取代了先前使用的發光強度（ $I$ ）。但在此之前，就有不少科學家質疑光度學是否真的需要一個特別的基本單位。此外，科學界已經公認，流明（ $lm$ ）是比坎德拉更為基礎的單位。然而為了國際單位制的連貫性，新制仍保留了坎德拉這一基本單位。[74]

參見

備註

1983年，米再次修訂為基於光速的單位。2019年的提案保留了此定義。
8(41)號公斤原器被誤標為41號，但它所攜帶的所有配件皆正確標為8號，因此這件原器今天的編號記作8(41)。
其中一項條件是，國際計量委員會必須為第23屆國際計量大會上定下的公斤、安培、開爾文和摩爾的新定義分別提供詳細的現實測量方法。[29]
有關非國際單位制單位的表格8的一項腳註寫道：「道爾頓（Da）和統一原子質量單位（u）指的是同一個單位，相等於一顆自由碳-12原子靜止且處於基態時的質量。」
坎德拉比較特殊，要將發光效能的單位轉換為坎德拉，還需要一個描述人眼對不同波長的感測強度的模型。模型由光度函數表達，記作V(λ)，由國際照明委員會所判斷和頒布。
此處所用術語的詳細定義請見：International vocabulary of metrology – Basic and general concepts and associated terms （页面存档备份，存于）
- 測量可重現度（measurement reproducibility），定義2.25
- 標準測量不確定度（standard measurement uncertainty），定義2.30
- 相對標準測量不確定度（relative standard measurement uncertainty），定義2.32
亞佛加厥常數 $N A$ 和亞佛加厥數 $N N$ 儘管數值相同，但前者的單位是mol⁻¹，後者則不帶任何單位。

參考資料

(PDF). [2018-05-05]. （原始内容存档 (PDF)于2018-01-21）.
. [2017-08-31]. （原始内容存档于2017-08-24）.
Kühne, Michael. . Keynote address, ITS⁹ (Ninth International Temperature Symposium). Los Angeles: NIST. 2012-03-22 [2012-03-01]. （原始内容存档于2013-06-18）.
. BIPM. 2019 [2019-05-20]. （原始内容存档于2021-01-18）.
(PDF). International Committee for Weights and Measures. Sèvres. 2017-10-20 [2018-01-27]. （原始内容存档 (PDF)于2018-01-27）.
. NIST. 2018-11-16 [2018-11-16]. （原始内容存档于2018-11-18）.
Milton, Martin. (PDF). SIM XXII General Assembly. Montevideo, Uruguay: 10. 2016-11-14 [2017-01-13]. （原始内容 (PDF)存档于2017-09-01）.大會在11月13至16日舉行，各代表在最後一天投票決議。哈薩克斯坦代表缺席。
Crease, Robert P. . . New York: W. W. Norton & Company, Inc. 2011: 83–84. ISBN 978-0-393-07298-3.
Alder, Ken. . London: Abacus. 2002: 1. ISBN 978-0-349-11507-8.
. Washington, D.C.: Office of the President of the United States. 1876 [2020-05-21]. （原始内容存档于2005-03-01）.
. Sèvres, France: International Bureau of Weights and Measures. [2013-06-21]. （原始内容存档于2012-09-26）.
. Sèvres, France: BIPM. [2010-10-03]. （原始内容存档于2012-09-24）.
. Sèvres, France: International Bureau of Weights and Measures. [2013-06-21]. （原始内容存档于2013-05-21）.
Jabbour, Z.J.; Yaniv, S.L. (PDF). Journal of Research of the National Institute of Standards and Technology. 2001, 106 (1): 25–46 [2011-03-28]. PMC 4865288 . PMID 27500016. doi:10.6028/jres.106.003. （原始内容 (PDF)存档于2011-06-04）.
International Bureau of Weights and Measures, (PDF) 8th: 95, 97, 138–140, 2006 [2020-05-21], ISBN 92-822-2213-6, （原始内容存档 (PDF)于2017-08-14）
. [2011-03-23]. （原始内容存档于2013-05-14）.
. Sèvres, France. [2011-03-23]. （原始内容存档于2013-04-14）.
Stephenson, F. R.; Morrison, L. V.; Hohenkerk, C. Y. . Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2016-12, 472 (2196). §4(a). Bibcode:2016RSPSA.47260404S. PMC 5247521 . PMID 28119545. doi:10.1098/rspa.2016.0404.
International Bureau of Weights and Measures, (PDF) 8th: 112–116, 2006 [2020-05-21], ISBN 92-822-2213-6, （原始内容存档 (PDF)于2017-08-14）
Girard, G. . Metrologia. 1994, 31 (4): 317–336. Bibcode:1994Metro..31..317G. doi:10.1088/0026-1394/31/4/007.
Peter, Mohr. (PDF). Third Workshop on Precision Physics and Fundamental Physical Constant. 2010-12-06 [2011-01-02]. （原始内容存档 (PDF)于2011-08-24）.
Whipple, Tom. . The Times (London). 2013-01-07: 15 [2011-03-23]. （原始内容存档于2013-01-17）.
Ghose, Tia. . LiveScience. 2013-01-06 [2011-03-23]. （原始内容存档于2013-03-26）.
Crease, Robert P. . Physics World. 2011-03-22, 24 (3): 39–45 [2012-06-28]. Bibcode:2011PhyW...24c..39C. doi:10.1088/2058-7058/24/03/34. （原始内容存档于2020-04-27）.
Fischer, J.; et al. (PDF). 2007-05-02 [2011-01-02]. （原始内容存档 (PDF)于2008-11-23）.
(PDF). International Union of Pure and Applied Physics. 2008 [2015-09-06]. （原始内容存档 (PDF)于2016-03-05）.
Mills, Ian. (PDF). CCU. 2010-09-29 [2011-01-01]. （原始内容存档 (PDF)于2012-01-13）.
Mills, Ian. (PDF). CCU. 2010-09-29 [2011-01-01]. （原始内容存档 (PDF)于2013-06-23）.
. Sèvres, France: General Conference on Weights and Measures. [2013-06-21]. （原始内容存档于2013-04-21）.
. International Bureau of Weights and Measures (BIPM). [2011-02-20]. （原始内容存档于2011-05-14）.
(PDF). International Committee for Weights and Measures (CIPM). [2011-07-14]. （原始内容存档 (PDF)于2011-08-06）.
(PDF). . Sèvres, France: International Bureau for Weights and Measures. 2011-10-21 [2020-05-21]. （原始内容存档 (PDF)于2012-01-13）.新定義至少在2014年之前不會生效，參見：. IUPAC Wire. 2012-02, 34 (1).
(PDF) (新闻稿). Sèvres, France: General Conference on Weights and Measures. 2011-10-23 [2011-10-25]. （原始内容存档 (PDF)于2012-02-09）.
Mohr, Peter. . NIST Newsletter. NIST. 2011-11-02 [2012-03-01]. （原始内容存档于2016-08-12）.
(PDF). Sèvres, France: International Bureau for Weights and Measures. 2014-11-21 [2014-12-01]. （原始内容存档 (PDF)于2015-03-25）.
(PDF). [2018-05-05]. （原始内容存档 (PDF)于2018-04-29）.
Newell, David B.; Cabiati, F.; Fischer, J.; Fujii, K.; Karshenboim, S.G.; Margolis, H.S.; de Mirandés, E.; Mohr, P.J.; Nez, F.; Pachucki, K.; Quinn, T.J.; Taylor, B.N.; Wang, M.; Wood, B.M.; Zhang, Z. . Metrologia. 2017-10-20, 55 (1): L13. Bibcode:2018Metro..55L..13N. doi:10.1088/1681-7575/aa950a.
. Chemistry International -- Newsmagazine for IUPAC. 2011-01, 33 (5) [2022-01-20]. ISSN 1365-2192. doi:10.1515/ci.2011.33.5.12. （原始内容存档于2022-01-20）.
Travenor, Robert. . Yale University Press. 2007: 35–36. ISBN 978-0-300-14334-8.
. International Bureau of Weights and Measures. 2012 [2013-03-28]. （原始内容存档于2013-04-21）.
Taylor, Barry N. . Journal of Research of the National Institute of Standards and Technology. 2011-12, 116 (6): 797–80. PMC 4551220 . PMID 26989600. doi:10.6028/jres.116.022.
Taylor, Barry N; Mohr, Peter J. . Metrologia. 1999-11, 36 (1): 63–64. Bibcode:1999Metro..36...63T. doi:10.1088/0026-1394/36/1/11.
. Historical context of the SI. NIST. [2015-09-07]. （原始内容存档于2013-06-27）.
Orfanidis, Sophocles J. (PDF). ECE Department, Rutgers University. 2010-08-31. 1.3 Constitutive Relations [2013-06-24]. （原始内容存档 (PDF)于2013-09-15）.
Chyla, W.T. . Acta Physica Polonica A. 2011-12, 120 (6): 998–1011. doi:10.12693/APhysPolA.120.998.
Davis, Richard S. . American Journal of Physics. 2017, 85 (5): 364–368. Bibcode:2017AmJPh..85..364D. arXiv:1610.02910 . doi:10.1119/1.4976701.
. NIST. NIST. 2018-10-23 [2018-10-24]. （原始内容存档于2018-10-24）.
(PDF). Bureau international des poids et mesures. 2018-11 [2020-02-04]. （原始内容存档 (PDF)于2020-02-04）.
Nawrocki, Waldemar. . Springer. 2019-05-30: 54 [2020-05-21]. ISBN 978-3-030-19677-6. （原始内容存档于2020-07-24）（英语）.
Wyszecki, G.; Blevin, W.R.; Kessler, K.G.; Mielenz, K.D. (PDF). Sevres: Conférence général des poids et mesures (CGPM). 1983 [2012-04-23]. （原始内容存档 (PDF)于2008-10-11）.
. BIPM. 2011 [2015-09-06]. （原始内容存档于2015-09-22）. is a set of instructions that allows the definition to be realised in practice at the highest level.
(PDF). 12th Meeting of the CCM. Sèvres: Bureau International des Poids et Mesures. 2010-03-26 [2012-06-27]. （原始内容 (PDF)存档于2013-05-14）.
(PDF). 16th Meeting of the CCQM. Sèvres: Bureau International des Poids et Mesures. 2010-04-16 [2012-06-27]. （原始内容 (PDF)存档于2013-05-14）.
(PDF). 25th Meeting of the Consultative Committee for Thermometry. Sèvres: Bureau International des Poids et Mesures. 2010-05-07 [2012-06-27]. （原始内容 (PDF)存档于2013-05-14）.
. European Association of National Metrology Institutes. [2012-10-08]. （原始内容存档于2016-03-04）.
Mohr, Peter J. 53. Academic Press. 2008: 34 [2012-04-02]. Bibcode:2008AdQC...53...27M. ISBN 978-0-12-373925-4. doi:10.1016/s0065-3276(07)53003-0. |journal=被忽略 (帮助)
(新闻稿). NIST. 2016-11-22 [2016-12-31]. （原始内容存档于2017-01-01）.
Mohr, Peter J.; Newell, David B.; Taylor, Barry N. . Reviews of Modern Physics. 2016-09-26, 88 (3): 035009–1–73. Bibcode:2016RvMP...88c5009M. arXiv:1507.07956 . doi:10.1103/RevModPhys.88.035009. This is a truly major development, because these uncertainties are now sufficiently small that the adoption of the new SI by the 26th CGPM is expected.
Conover, Emily. . Science News. 2018-11-16 [2018-11-16]. （原始内容存档于2018-11-16）.
Foster, Marcus P. . Metrologia. 2010-10-05, 47 (6): R41–R51 [2013-06-24]. Bibcode:2010Metro..47R..41F. doi:10.1088/0026-1394/47/6/R01. （原始内容存档于2016-03-06）.
Price, Gary. . Accreditation and Quality Assurance. 2011-03, 16 (3): 121–132. ISSN 0949-1775. doi:10.1007/s00769-010-0738-x （英语）.
Censullo, Albert C. . Chemistry International. 2011-10, 33 (5): 9–12 [2013-06-28]. ISSN 0193-6484. （原始内容存档于2017-07-09）.
Burns, D Thorburn; Korte, EH. (PDF). Journal of the Association of Public Analysts (Online). 2013, (41 2): 28–44 [2013-06-25]. （原始内容存档 (PDF)于2016-03-06）.
Davis, Richard. (PDF). OIML Bulletin. 2011-10, LII (4) [2013-06-28]. （原始内容存档 (PDF)于2015-03-27）.
Johansson, Ingvar. . Accreditation and Quality Assurance. 2011-08, 16 (8-9): 467–470. ISSN 0949-1775. doi:10.1007/s00769-011-0804-z （英语）.
http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf （页面存档备份，存于） SI Brochure (8th edition)
Leonard, B.P. . Metrologia. 2010, 47 (3): L5–L8. Bibcode:2010Metro..47L...5L. doi:10.1088/0026-1394/47/3/L01.
Pavese, Franco. . Accreditation and Quality Assurance. 2011-03, 16 (3): 161–165. ISSN 0949-1775. doi:10.1007/s00769-010-0700-y （英语）.
Mills, Ian; Cvitaš, Tomislav; Homann, Klaus; Kallay, Nikola; Kuchitsu, Kozo. 2nd. International Union of Pure and Applied Chemistry, Blackwell Science Ltd. 1993. ISBN 978-0-632-03583-0.
International Bureau of Weights and Measures, (PDF) 8th: 114, 115, 2006 [2020-05-21], ISBN 92-822-2213-6, （原始内容存档 (PDF)于2017-08-14）
Leonard, Brian Phillip. . Metrologia. 2012-05, 49 (4): 487–491. Bibcode:2012Metro..49..487L. doi:10.1088/0026-1394/49/4/487.
(PDF). Sèvres, France: Consultative Committee for Thermometry (CCT), International Committee for Weights and Measures (CIPM). 2011 [2013-06-25]. （原始内容存档 (PDF)于2013-05-08）.
Consultative Committee for Thermometry (CCT). (PDF). Procès-verbaux du Comité International des Poids et Mesures, 78th Meeting. 1989 [2013-06-25]. （原始内容存档 (PDF)于2013-06-23）.
(PDF). Procès-verbaux du Comité International des Poids et Mesures, 66th Meeting. 1977: 14, 143 [2019-09-01]. （原始内容存档 (PDF)于2021-01-10）（法语）.

延伸閱讀

International Bureau of Weights and Measures, (PDF) 9th, 2019-05-20 [2020-05-21], ISBN 978-92-822-2272-0, （原始内容存档 (PDF)于2020-05-19）
International Bureau of Weights and Measures (BIPM). . Metrologia Updated. 2017-08-10 [2017-08-14]. （原始内容存档于2018-10-05）.

外部連結

國際計量局有關國際單位制新定義的網頁（页面存档备份，存于）、常見問題網頁（页面存档备份，存于）

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[8] 1983年，米再次修訂為基於光速的單位。2019年的提案保留了此定義。

[21] 8(41)號公斤原器被誤標為41號，但它所攜帶的所有配件皆正確標為8號，因此這件原器今天的編號記作8(41)。

[32] 其中一項條件是，國際計量委員會必須為第23屆國際計量大會上定下的公斤、安培、開爾文和摩爾的新定義分別提供詳細的現實測量方法。[29]

[51] 有關非國際單位制單位的表格8的一項腳註寫道：「道爾頓（Da）和統一原子質量單位（u）指的是同一個單位，相等於一顆自由碳-12原子靜止且處於基態時的質量。」

[CandelaNote-54] 坎德拉比較特殊，要將發光效能的單位轉換為坎德拉，還需要一個描述人眼對不同波長的感測強度的模型。模型由光度函數表達，記作V(λ)，由國際照明委員會所判斷和頒布。

[VIM-56] 此處所用術語的詳細定義請見：International vocabulary of metrology – Basic and general concepts and associated terms （页面存档备份，存于）
測量可重現度（measurement reproducibility），定義2.25

標準測量不確定度（standard measurement uncertainty），定義2.30

相對標準測量不確定度（relative standard measurement uncertainty），定義2.32

[7] 測量可重現度（measurement reproducibility），定義2.25

[8] 標準測量不確定度（standard measurement uncertainty），定義2.30

[9] 相對標準測量不確定度（relative standard measurement uncertainty），定義2.32

[71] 亞佛加厥常數 $N A$ 和亞佛加厥數 $N N$ 儘管數值相同，但前者的單位是mol⁻¹，後者則不帶任何單位。

[SI-statement-1] (PDF). [2018-05-05]. （原始内容存档 (PDF)于2018-01-21）.

[2] . [2017-08-31]. （原始内容存档于2017-08-24）.

[Kuehne-3] Kühne, Michael. . Keynote address, ITS⁹ (Ninth International Temperature Symposium). Los Angeles: NIST. 2012-03-22 [2012-03-01]. （原始内容存档于2013-06-18）.

[Brochure9_2019-4] . BIPM. 2019 [2019-05-20]. （原始内容存档于2021-01-18）.

[cipm_106-5] (PDF). International Committee for Weights and Measures. Sèvres. 2017-10-20 [2018-01-27]. （原始内容存档 (PDF)于2018-01-27）.

[6] . NIST. 2018-11-16 [2018-11-16]. （原始内容存档于2018-11-18）.

[Milton16-7] Milton, Martin. (PDF). SIM XXII General Assembly. Montevideo, Uruguay: 10. 2016-11-14 [2017-01-13]. （原始内容 (PDF)存档于2017-09-01）.大會在11月13至16日舉行，各代表在最後一天投票決議。哈薩克斯坦代表缺席。

[9] Crease, Robert P. . . New York: W. W. Norton & Company, Inc. 2011: 83–84. ISBN 978-0-393-07298-3.

[10] Alder, Ken. . London: Abacus. 2002: 1. ISBN 978-0-349-11507-8.

[11] . Washington, D.C.: Office of the President of the United States. 1876 [2020-05-21]. （原始内容存档于2005-03-01）.

[12] . Sèvres, France: International Bureau of Weights and Measures. [2013-06-21]. （原始内容存档于2012-09-26）.

[13] . Sèvres, France: BIPM. [2010-10-03]. （原始内容存档于2012-09-24）.

[14] . Sèvres, France: International Bureau of Weights and Measures. [2013-06-21]. （原始内容存档于2013-05-21）.

[15] Jabbour, Z.J.; Yaniv, S.L. (PDF). Journal of Research of the National Institute of Standards and Technology. 2001, 106 (1): 25–46 [2011-03-28]. PMC 4865288 . PMID 27500016. doi:10.6028/jres.106.003. （原始内容 (PDF)存档于2011-06-04）.

[16] International Bureau of Weights and Measures, (PDF) 8th: 95, 97, 138–140, 2006 [2020-05-21], ISBN 92-822-2213-6, （原始内容存档 (PDF)于2017-08-14）

[17] . [2011-03-23]. （原始内容存档于2013-05-14）.

[18] . Sèvres, France. [2011-03-23]. （原始内容存档于2013-04-14）.

[19] Stephenson, F. R.; Morrison, L. V.; Hohenkerk, C. Y. . Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2016-12, 472 (2196). §4(a). Bibcode:2016RSPSA.47260404S. PMC 5247521 . PMID 28119545. doi:10.1098/rspa.2016.0404.

[BaseDefs-20] International Bureau of Weights and Measures, (PDF) 8th: 112–116, 2006 [2020-05-21], ISBN 92-822-2213-6, （原始内容存档 (PDF)于2017-08-14）

[Girard-22] Girard, G. . Metrologia. 1994, 31 (4): 317–336. Bibcode:1994Metro..31..317G. doi:10.1088/0026-1394/31/4/007.

[23] Peter, Mohr. (PDF). Third Workshop on Precision Physics and Fundamental Physical Constant. 2010-12-06 [2011-01-02]. （原始内容存档 (PDF)于2011-08-24）.

[24] Whipple, Tom. . The Times (London). 2013-01-07: 15 [2011-03-23]. （原始内容存档于2013-01-17）.

[25] Ghose, Tia. . LiveScience. 2013-01-06 [2011-03-23]. （原始内容存档于2013-03-26）.

[Crease-26] Crease, Robert P. . Physics World. 2011-03-22, 24 (3): 39–45 [2012-06-28]. Bibcode:2011PhyW...24c..39C. doi:10.1088/2058-7058/24/03/34. （原始内容存档于2020-04-27）.

[27] Fischer, J.; et al. (PDF). 2007-05-02 [2011-01-02]. （原始内容存档 (PDF)于2008-11-23）.

[28] (PDF). International Union of Pure and Applied Physics. 2008 [2015-09-06]. （原始内容存档 (PDF)于2016-03-05）.

[29] Mills, Ian. (PDF). CCU. 2010-09-29 [2011-01-01]. （原始内容存档 (PDF)于2012-01-13）.

[draft-30] Mills, Ian. (PDF). CCU. 2010-09-29 [2011-01-01]. （原始内容存档 (PDF)于2013-06-23）.

[31] . Sèvres, France: General Conference on Weights and Measures. [2013-06-21]. （原始内容存档于2013-04-21）.

[33] . International Bureau of Weights and Measures (BIPM). [2011-02-20]. （原始内容存档于2011-05-14）.

[34] (PDF). International Committee for Weights and Measures (CIPM). [2011-07-14]. （原始内容存档 (PDF)于2011-08-06）.

[Resolution-35] (PDF). . Sèvres, France: International Bureau for Weights and Measures. 2011-10-21 [2020-05-21]. （原始内容存档 (PDF)于2012-01-13）.新定義至少在2014年之前不會生效，參見：. IUPAC Wire. 2012-02, 34 (1).

[36] (PDF) (新闻稿). Sèvres, France: General Conference on Weights and Measures. 2011-10-23 [2011-10-25]. （原始内容存档 (PDF)于2012-02-09）.

[Mohr-37] Mohr, Peter. . NIST Newsletter. NIST. 2011-11-02 [2012-03-01]. （原始内容存档于2016-08-12）.

[38] (PDF). Sèvres, France: International Bureau for Weights and Measures. 2014-11-21 [2014-12-01]. （原始内容存档 (PDF)于2015-03-25）.

[draft-resolution-A-39] (PDF). [2018-05-05]. （原始内容存档 (PDF)于2018-04-29）.

[codata_2017-40] Newell, David B.; Cabiati, F.; Fischer, J.; Fujii, K.; Karshenboim, S.G.; Margolis, H.S.; de Mirandés, E.; Mohr, P.J.; Nez, F.; Pachucki, K.; Quinn, T.J.; Taylor, B.N.; Wang, M.; Wood, B.M.; Zhang, Z. . Metrologia. 2017-10-20, 55 (1): L13. Bibcode:2018Metro..55L..13N. doi:10.1088/1681-7575/aa950a.

[41] . Chemistry International -- Newsmagazine for IUPAC. 2011-01, 33 (5) [2022-01-20]. ISSN 1365-2192. doi:10.1515/ci.2011.33.5.12. （原始内容存档于2022-01-20）.

[Smoot-42] Travenor, Robert. . Yale University Press. 2007: 35–36. ISBN 978-0-300-14334-8.

[BIPMwatt-43] . International Bureau of Weights and Measures. 2012 [2013-03-28]. （原始内容存档于2013-04-21）.

[Barry-44] Taylor, Barry N. . Journal of Research of the National Institute of Standards and Technology. 2011-12, 116 (6): 797–80. PMC 4551220 . PMID 26989600. doi:10.6028/jres.116.022.

[45] Taylor, Barry N; Mohr, Peter J. . Metrologia. 1999-11, 36 (1): 63–64. Bibcode:1999Metro..36...63T. doi:10.1088/0026-1394/36/1/11.

[46] . Historical context of the SI. NIST. [2015-09-07]. （原始内容存档于2013-06-27）.

[47] Orfanidis, Sophocles J. (PDF). ECE Department, Rutgers University. 2010-08-31. 1.3 Constitutive Relations [2013-06-24]. （原始内容存档 (PDF)于2013-09-15）.

[Chyla-48] Chyla, W.T. . Acta Physica Polonica A. 2011-12, 120 (6): 998–1011. doi:10.12693/APhysPolA.120.998.

[Davis-AJP-49] Davis, Richard S. . American Journal of Physics. 2017, 85 (5): 364–368. Bibcode:2017AmJPh..85..364D. arXiv:1610.02910 . doi:10.1119/1.4976701.

[50] . NIST. NIST. 2018-10-23 [2018-10-24]. （原始内容存档于2018-10-24）.

[52] (PDF). Bureau international des poids et mesures. 2018-11 [2020-02-04]. （原始内容存档 (PDF)于2020-02-04）.

[53] Nawrocki, Waldemar. . Springer. 2019-05-30: 54 [2020-05-21]. ISBN 978-3-030-19677-6. （原始内容存档于2020-07-24）（英语）.

[55] Wyszecki, G.; Blevin, W.R.; Kessler, K.G.; Mielenz, K.D. (PDF). Sevres: Conférence général des poids et mesures (CGPM). 1983 [2012-04-23]. （原始内容存档 (PDF)于2008-10-11）.

[57] . BIPM. 2011 [2015-09-06]. （原始内容存档于2015-09-22）. is a set of instructions that allows the definition to be realised in practice at the highest level.

[58] (PDF). 12th Meeting of the CCM. Sèvres: Bureau International des Poids et Mesures. 2010-03-26 [2012-06-27]. （原始内容 (PDF)存档于2013-05-14）.

[59] (PDF). 16th Meeting of the CCQM. Sèvres: Bureau International des Poids et Mesures. 2010-04-16 [2012-06-27]. （原始内容 (PDF)存档于2013-05-14）.

[60] (PDF). 25th Meeting of the Consultative Committee for Thermometry. Sèvres: Bureau International des Poids et Mesures. 2010-05-07 [2012-06-27]. （原始内容 (PDF)存档于2013-05-14）.

[61] . European Association of National Metrology Institutes. [2012-10-08]. （原始内容存档于2016-03-04）.

[62] Mohr, Peter J. 53. Academic Press. 2008: 34 [2012-04-02]. Bibcode:2008AdQC...53...27M. ISBN 978-0-12-373925-4. doi:10.1016/s0065-3276(07)53003-0. |journal=被忽略 (帮助)

[NIST16-63] (新闻稿). NIST. 2016-11-22 [2016-12-31]. （原始内容存档于2017-01-01）.

[CODATA2014-64] Mohr, Peter J.; Newell, David B.; Taylor, Barry N. . Reviews of Modern Physics. 2016-09-26, 88 (3): 035009–1–73. Bibcode:2016RvMP...88c5009M. arXiv:1507.07956 . doi:10.1103/RevModPhys.88.035009. This is a truly major development, because these uncertainties are now sufficiently small that the adoption of the new SI by the 26th CGPM is expected.

[65] Conover, Emily. . Science News. 2018-11-16 [2018-11-16]. （原始内容存档于2018-11-16）.

[Foster-66] Foster, Marcus P. . Metrologia. 2010-10-05, 47 (6): R41–R51 [2013-06-24]. Bibcode:2010Metro..47R..41F. doi:10.1088/0026-1394/47/6/R01. （原始内容存档于2016-03-06）.

[67] Price, Gary. . Accreditation and Quality Assurance. 2011-03, 16 (3): 121–132. ISSN 0949-1775. doi:10.1007/s00769-010-0738-x （英语）.

[68] Censullo, Albert C. . Chemistry International. 2011-10, 33 (5): 9–12 [2013-06-28]. ISSN 0193-6484. （原始内容存档于2017-07-09）.

[69] Burns, D Thorburn; Korte, EH. (PDF). Journal of the Association of Public Analysts (Online). 2013, (41 2): 28–44 [2013-06-25]. （原始内容存档 (PDF)于2016-03-06）.

[70] Davis, Richard. (PDF). OIML Bulletin. 2011-10, LII (4) [2013-06-28]. （原始内容存档 (PDF)于2015-03-27）.

[72] Johansson, Ingvar. . Accreditation and Quality Assurance. 2011-08, 16 (8-9): 467–470. ISSN 0949-1775. doi:10.1007/s00769-011-0804-z （英语）.

[73] ttp://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf （页面存档备份，存于） SI Brochure (8th edition)

[74] Leonard, B.P. . Metrologia. 2010, 47 (3): L5–L8. Bibcode:2010Metro..47L...5L. doi:10.1088/0026-1394/47/3/L01.

[75] Pavese, Franco. . Accreditation and Quality Assurance. 2011-03, 16 (3): 161–165. ISSN 0949-1775. doi:10.1007/s00769-010-0700-y （英语）.

[76] Mills, Ian; Cvitaš, Tomislav; Homann, Klaus; Kallay, Nikola; Kuchitsu, Kozo. 2nd. International Union of Pure and Applied Chemistry, Blackwell Science Ltd. 1993. ISBN 978-0-632-03583-0.

[77] International Bureau of Weights and Measures, (PDF) 8th: 114, 115, 2006 [2020-05-21], ISBN 92-822-2213-6, （原始内容存档 (PDF)于2017-08-14）

[78] Leonard, Brian Phillip. . Metrologia. 2012-05, 49 (4): 487–491. Bibcode:2012Metro..49..487L. doi:10.1088/0026-1394/49/4/487.

[79] (PDF). Sèvres, France: Consultative Committee for Thermometry (CCT), International Committee for Weights and Measures (CIPM). 2011 [2013-06-25]. （原始内容存档 (PDF)于2013-05-08）.

[80] Consultative Committee for Thermometry (CCT). (PDF). Procès-verbaux du Comité International des Poids et Mesures, 78th Meeting. 1989 [2013-06-25]. （原始内容存档 (PDF)于2013-06-23）.

[81] (PDF). Procès-verbaux du Comité International des Poids et Mesures, 66th Meeting. 1977: 14, 143 [2019-09-01]. （原始内容存档 (PDF)于2021-01-10）（法语）.