布拉格定律
在物理學中,布拉格定律給出晶格的相干及不相干散射角度。當X射線入射於原子時,跟任何電磁波一樣,它們會使電子雲移動。電荷的運動把波動以同樣的頻率再發射出去(會因其他各種效應而變得有點模糊);這種現象叫瑞利散射(或彈性散射)。散射出來的波可以再相互散射,但這種進級散射在這裏是可以忽略的。當中子波與原子核或不成對電子的相干自旋進行相互作用時,會發生一種與上述電磁波相近的過程。這些被重新發射出來的波來相互干涉,可能是相長的,也可能是相消的(重疊的波某程度上會加起來產生更強的波峰,或相互消抵),在探測器或底片上產生繞射圖樣。而所產生的波干涉圖樣就是繞射分析的基本部份。這種解析叫布拉格繞射。
布拉格繞射(又稱X射線繞射的布拉格形式),最早由威廉·勞倫斯·布拉格及威廉·亨利·布拉格於1913年提出,他們早前發現了固體在反射X射線後產生的晶體線(與其他物態不同,例如液體),而這項定律正好解釋了這樣一種效應。他們發現,這些晶體在特定的波長及入射角時,反射出來的輻射會形成集中的波峰(叫布拉格尖峰)。布拉格繞射這個概念同樣適用於中子繞射及電子繞射 [1] 。中子及X射線的波長都於原子間距離(~150 pm)相若,因此它們很適合在這種長度作“探針”之用。

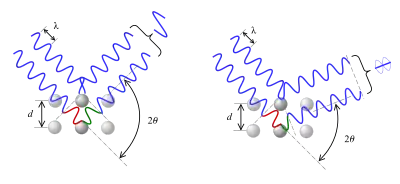
威廉·勞倫斯·布拉格使用了一個模型來解釋這個結果,模型中晶體為一組各自分離的平行平面,相鄰平面間的距離皆為一常數d。他的解釋是,如果各平面反射出來的X射線成相長干涉的話,那麼入射的X射線經晶體反射後會產生布拉格尖峰。當相位差為2π及其倍數時,干涉為相長的;這個條件可經由布拉格定律表示[2]:
其中n為整數,λ為入射波的波長,d為原子晶格內的平面間距,而θ則為入射波與散射平面間的夾角。注意移動中的粒子,包括電子、質子和中子,都有對應其速度及質量的德布羅意波長。
布拉格定律由物理學家威廉·勞倫斯·布拉格爵士[3]於1912年推導出來,並於1912年11月11日首度於劍橋哲學會中發表。儘管很簡單,布拉格定律確立了粒子在原子大小下的存在,同時亦為晶體研究提供了有效的新工具──X射線及中子繞射。威廉·勞倫斯·布拉格及其父,威廉·亨利·布拉格爵士獲授1915年諾貝爾物理學獎,原因為晶體結構測定的研究,他們測定了氯化鈉、硫化鋅及鑽石的結構。 他們是唯一一隊同時獲獎的父子隊伍,而威廉·勞倫斯·布拉格時年25歲,因此成了最年輕的諾貝爾獎得主。
布拉格條件

當電磁輻射或亞原子粒子波的波長,與進入的晶體樣本的原子間距長度相若時,就會產生布拉格繞射,入射物會被系統中的原子以鏡面形式散射出去,並會按照布拉格定律所示,進行相長干涉。對於晶質固體,波被晶格平面所散射,各相鄰平面間的距離為d。當被各平面散射出去的波進行相長干涉時,它們的相位依然相同,因此每一波的路徑長度皆為波長的整數倍。進行相長干涉兩波的路徑差為,其中為散射角。由此可得布拉格定律,它所描述的是晶格中相鄰晶體平面(由米勒指數h、k及l 標記),產生相長干涉的條件[4] :
- ,
其中n為整數,按各項參數大小而定,而λ則為波長[5]。通過量度散射後入射波的強度,並將之表示成入射角的函數,可得干涉圖樣。在干涉圖樣中,當散射波滿足布拉格條件,就會產生非常強的強度,它們叫布拉格尖峰。
倒空間
儘管很多人都以為布拉格定律量度的是實空間中的原子距離,但事實並不是這樣的。在布拉格實驗中,只有在量度的距離與晶格圖中的d成反比時,第一陳述才似乎會是正確的。而且,從布拉格定律的項,可以看出定律量度兩排原子間到底能放多少個波長,因此它所量度的是倒距離。倒晶格向量描述的是某組晶格平面,它是這組平面的法向量,其長度為。馬克斯·馮·勞厄用向量形式正確地詮釋了倒晶格向量,並得出以他命名的勞厄方程式:
其中為倒晶格向量,而及為入射及繞射束的波向量。
彈性散射條件,及散射角與上式結合後,基本上與布拉格方程等效。這是因為動量轉移守恆的緣故。在這個系統中,其掃掠變量可以是長度、入射方向或出射波向量,其中波向量與系統中的能量及角度彌散有關。繞射角與Q空間的關係可用一簡單的式子表示:
- 。
倒晶格是一晶格的傅立葉空間,在晶格上應用完整的波動力學時,這個概念是不可或缺的。
另一種推導
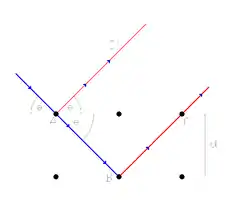
設一單色波(任何種類),進入一組對齊的平面晶格點,其平面間距為,入射角為,如右圖所示。波被晶格點A反射後會沿AC'行進,而沒有被反射的波則沿AB繼續行進,被晶格點B反射後路徑為BC。AC'與BC間存在路徑差,表達式為
- 。
只有在路徑差等於波長的整數倍時,這兩股分開的波,在到達某一點時,會是同相位的,才會因此產生相長干涉,故相長干涉的產生條件為
- , (需要為C'下定義)
其中與的定義同上。
從上圖可見,
- 且 ,
由此可得,
- 。
組合上述各式,得
- ,
簡化後可得:
- ,
即布拉格定律。
膠體晶體的布拉格可見光散射
膠體晶體為一種非常有序的粒子陣列,可以在大範圍內形成(長度從幾微米到幾毫米不等),而且可被看作原子及分子晶體的類比[6]。球狀粒子的週期性陣列,會形成出相似的空隙陣列,而這種陣列可被用作可見光的繞射光柵,尤其是當空隙與入射波長為同一數量級的時候[7][8][9]。
因此,科學家們在很多年前就發現了,由於相斥庫侖相互作用的關係,水溶液中的帶電荷高分子,會表現出大範圍的類晶體相互關聯,當中粒子間距一般會比粒子直徑要大得多。在自然的所有這種例子中,都可到看到一樣的漂亮構造色(或晃動的色彩),這都可以歸功於可見光波的相長干涉,而此時光波會滿足布拉格條件,跟結晶固體的X射線繞射類似。
選擇定則與實驗晶體學
就跟上文提過的那樣,布拉格定律可用於計算某立方晶系的晶格間距,關係式如下:
其中為立方晶體的晶格間距,而、及則為布拉格平面的密勒指數,將上式與布拉格定律結合可得:
- 。
我們可以推導出各種不同立方布拉菲晶格的密勒指數選擇定則;以下是其種幾種晶格的選擇定則。
| 布拉菲晶格 | 化合物例子 | 可行反射 | 不可行反射 |
|---|---|---|---|
| 簡單立方 | 釙、氯化鉀 | 任何h、k、l | 無 |
| 體心立方 | 鐵、鎢、鉭、鉻 | h + k + l 為偶數 | h + k + l 為奇數 |
| 面心立方 | 銅、鋁、鎳、氯化鈉、氫化鋰、硫化鉛 | h、k、l皆為奇數或偶數 | h、k、l當中有奇數也有偶數 |
| 金刚石型 | 硒化鋅、氯化銅、碘化銀、氟化銅、硅、鍺 | 皆為奇數,或皆為偶數且h+k+l = 4n | 同上,或皆為偶數但h+k+l ≠ 4n |
| 三角点阵 | 鈦、鋯、鎘、鈹 | l為偶數或h + 2k ≠ 3n | l為奇數且h + 2k = 3n |
這些選擇定則可用於對應晶體結構下的任何晶體。儘管氯化鈉呈現面心立方的結構,但是由於氯離子跟鈉離子的大小相近,因此繞射圖樣實質上跟簡單立方結構一致,只是各項晶體參數都小了一半。其他結構的選擇定則可在各種相關的參考文獻中找到,也可以自行推導出來。
參考資料
- John M. Cowley (1975) Diffraction physics (North-Holland, Amsterdam) ISBN 0-444-10791-6.
- 例如,見使用布拉格定律計算原子間距離的例子 的存檔,存档日期2011-07-10.。
- 有一些資料來源,例如《美國學術百科》,把這項發現歸功於威廉·勞倫斯·布拉格及其父威廉·亨利·布拉格,然而 諾貝爾獎官方網站 (页面存档备份,存于)及關於他的傳記 ("Light Is a Messenger: The Life and Science of William Lawrence Bragg", Graeme K. Hunter, 2004 and "Great Solid State Physicists of the 20th Century", Julio Antonio Gonzalo, Carmen Aragó López) 都有明確指出,威廉·勞倫斯·布拉格是獨立地推導出這條定律的。
- H. P. Myers. . Taylor & Francis. 2002. ISBN 0-7484-0660-3.
- Carl. R. Nave. . HyperPhysics, Georgia State University. [2008-07-19]. (原始内容存档于2020-11-12).
- Pieranski, P. . Contemporary Physics. 1983, 24: 25. Bibcode:1983ConPh..24...25P. doi:10.1080/00107518308227471.
- Hiltner, PA; IM Krieger. . Journal of Physical Chemistry. 1969, 73: 2306.
- Aksay, IA. . Proceedings of the American Ceramic Society. 1984, 9: 94.
- Luck, W. et al., Ber. Busenges Phys. Chem. , Vol. 67, p.84 (1963)
延伸閱讀
- Neil W. Ashcroft and N. David Mermin, Solid State Physics (Harcourt: Orlando, 1976).
- Bragg, W.L. . Proceedings of the Cambridge Philosophical Society. 1913, 17: 43–57.