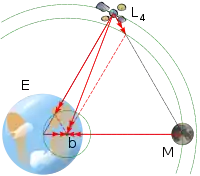
拉格朗日点
拉格朗日点(Lagrange point)又称平动点(libration points)在天体力学中是限制性三体问题的五个特殊解(particular solution)。就平面圆型三体问题,1767年数学家欧拉根据旋转的二体引力场推算出其中三个点為L1、L2、L3,1772年数学家拉格朗日推算出另外两个点(特解)為L4、L5。例如,两个天体环绕运行,在空间中有五个位置可以放入第三个物体(质量忽略不计),使其與另两个天体的相對位置保持不變。理想状态下,两个同轨道物体以相同的周期旋转,两个天体的万有引力在拉格朗日点平衡,使得第三个物体与前两个物体相对静止。
| 航天动力学 |
|---|
 |
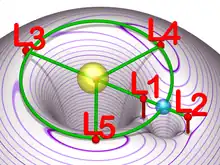
點擊觀看動畫
位置
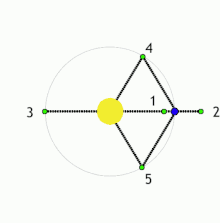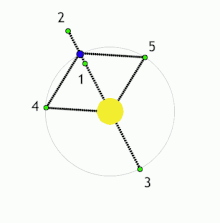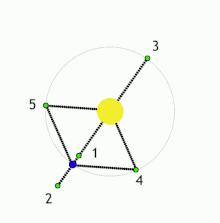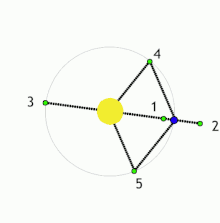
五个拉格朗日点之定义及位置如下:
L1
在M1和M2两个大天体的连线上,且在它们之间。
其中:r 表示 L1 与较小的物体之间的距离,R 表示两个主要物体之间的距离,M1 和 M2 分别表示较大物体和较小物体的质量。
求解 r 需要求解五次方程,但是当小物体的质量(M2)远小于大物体的质量(M1)时,L1和L2近似于希尔球的半径,求解如下:
例如一个围绕太阳旋转的物体,它距太阳的距离越近,它的轨道周期就越短。但是这忽略地球的万有引力对其产生的拉力的影响。如果这个物体在地球与太阳之间,地球引力的影响会减弱太阳对这物体的拉力,因此增加这个物体的轨道周期。物体距地球越近,这种影响就越大。在L1点,物体的轨道周期恰好等于地球的轨道周期。
太阳及日光层探测仪(SOHO)[2]即在日-地系统的L1点上运行。嫦娥五号的轨道器由于原登月任务完成后仍有充足的燃料,所以安排拓展任务,飞进到日-地系统的L1点进行进一步的太阳探测任务。
L2
在两个大天体的连线上,且在较小的天体一侧。
同样的,當小物体的质量(M2)远小于大物体的质量(M1)时:
日地系统的L2在地球远离太阳的一侧。一般来讲,一个物体距太阳的距离越远,它的轨道周期通常就越长,但L2点上的物体还受到地球的引力,所以轨道周期变得与地球的相等。日地系统的L2通常用于放置。因为L2上的物体可以保持背向太阳和地球的方位,易于保护和校准。威尔金森微波各向异性探测器已经在日-地系统的L2点上运行。詹姆斯韋伯太空望远镜也在日-地系统的L2点上。嫦娥二号亦於2011年进入日-地系统的L2点的环绕轨道,為从月球轨道出发進入日-地系统L2点的首例[3]。
地月系统的L2在月球远离地球的一侧(月球背面)。2014年中国探月工程三期再入返回飛行試驗器服务舱曾进入环绕地月L2点的李萨如轨道开展试验,服务舱实现了环绕地月L2点飞行三圈,验证了轨道设计、轨道控制和轨道维持技术[4]。之后嫦娥4号的通信中继卫星鹊桥号则是在该位置使用晕轮轨道维持运转。
L3
在两个大天体的连线上,且在较大的天体一侧。
- 例如:第三个拉格朗日点,L3,位于太阳的另一侧,與太陽的距離略小於地球與太陽的距離,但是位於地球軌道的外部,這個看上去矛盾的表述是因為地球公轉軌道的焦点,是太陽與地球的共同質心,儘管對於日地系統來說共同質心在太陽內部,太陽同時也在圍繞這個共同質心轉動,所以這種狀態成為可能。
平衡性
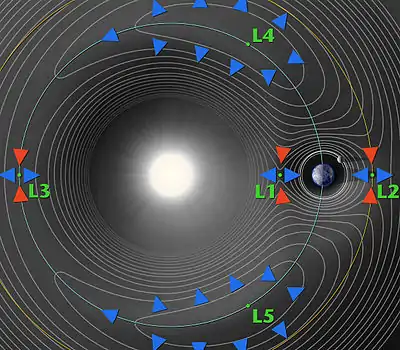
嚴格而言,首先拉格朗日點只算是二星體連線之法平面內的穩定點,而在三維空間內則不穩定:考慮L1:若垂直於中線地推移測試質點,則有一力將其推回平衡點(稳定平衡);但若測試質點漂向任一星體,則該星體之引力會將其拉向自己(不稳定平衡)。L1、L2和L3点在这条直线上不稳定,如果把物体放在这上面的话,它马上会离开这个点[5]。所以,有一种轨道的设计就是,它是围绕L2点做周期运动(晕轮轨道),这样的话,我们的卫星只需少量調節便能維持其軌道。
此對比:若M1比M2大於24.96[6],則处于L4與L5的物体是稳定平衡:當一測試質點偏離此平衡點,則科里奥利力會將其軌道扭曲成(相對於旋轉座標之)扁豆狀。太陽-木星系統有幾千枚小行星,通稱為「特洛伊小行星」,俱劃此等軌迹。太陽-火星、太陽-土星、木星-木衞、土星-土衞等系統亦有類似星體。日-地系統中亦有 2010 TK7(第一顆地球特洛伊小行星),在二十世紀五十年代發現塵霧圍繞L4與L5。在地-月系統之L4與L5點亦發現比对日照更微弱之塵霧。
流行文化
科幻作品(例如漫畫和小說)所說的放置殖民衛星的拉格朗日點指L4和L5,不包括L1和L2。例如L4和L5在地球圍太陽運行的軌道之前和之後成60°角處。
參考文獻
- Seidov, Zakir F. . The Astrophysical Journal. March 1, 2004, 603 (1): 283–284. Bibcode:2004ApJ...603..283S. arXiv:astro-ph/0311272
 . doi:10.1086/381315.
. doi:10.1086/381315. - . [2004-04-28]. (原始内容存档于2011-02-24).
- 王赤.科普:什么是拉格朗日点? (页面存档备份,存于)2013年01月24日
- (页面存档备份,存于) (页面存档备份,存于) (页面存档备份,存于) 我国航天器首次到达地月L2点 (页面存档备份,存于)南方日报.2015年01月06日
- 王赤:介绍拉格朗日点 (页面存档备份,存于)中国科学院.2011-09-25
- 关于拉格朗日点的介绍 的存檔,存档日期2003-06-05.
外部連結
- (英文)歐洲太空總署有關拉格朗日點的介紹和動畫 (页面存档备份,存于)