深度优先搜索
深度优先搜索算法(英語:,缩写为)是一种用于遍历或搜索树或图的算法。这个算法会尽可能深地搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。[1](p. 603)这种算法不会根据图的结构等信息调整执行策略。
| 深度优先搜索 | |
|---|---|
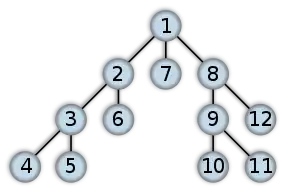 節點搜索的順序 節點進行深度优先搜索的順序 | |
| 概况 | |
| 類別 | 搜索演算法 |
| 資料結構 | 圖 |
| 复杂度 | |
| 平均時間複雜度 | |
| 空間複雜度 | |
| 最佳解 | 否 |
| 完全性 | 是 |
| 相关变量的定义 | |
| 分支係數 | |
| 圖的最大深度 | |
| 图与树 搜索算法 |
|---|
| 分类 |
|
| 相关主题 |
|
深度优先搜索是图论中的经典算法,利用深度优先搜索算法可以产生目标图的拓扑排序表[1](p. 612),利用拓扑排序表可以方便的解决很多相关的图论问题,如无权最长路径问题等等。
演算方法
- 首先将根节点放入stack中。
- 从stack中取出第一个节点,并检验它是否为目标。
- 如果找到目标,则结束搜寻并回传结果。
- 否则将它某一个尚未检验过的直接子节点加入stack中。
- 重复步骤2。
- 如果不存在未检测过的直接子节点。
- 将上一级节点加入stack中。
- 重复步骤2。
- 重复步骤4。
- 若stack为空,表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
C++的實作
定义一个结构体来表达一個二叉树的节点的结构:
struct Node {
int self; // 数据
Node *left; // 左孩子
Node *right; // 右孩子
};
那么我们在搜索一个树的时候,从一个节点开始,能首先获取的是它的两个子节点。例如:
A
B C
D E F G
|
A是第一个访问的,然后顺序是B和D、然后是E。然后再是C、F、G。那么我们怎么来保证这个顺序呢?
这里就应该用堆栈的结构,因为堆栈是一个后进先出(LIFO)的顺序。通过使用C++的STL,下面的程序能帮助理解:
const int TREE_SIZE = 9;
std::stack<Node *> unvisited;
Node nodes[TREE_SIZE];
Node *current;
//初始化树
for (int i = 0; i < TREE_SIZE; i++) {
nodes[i].self = i;
int child = i * 2 + 1;
if (child < TREE_SIZE) // Left child
nodes[i].left = &nodes[child];
else
nodes[i].left = NULL;
child++;
if (child < TREE_SIZE) // Right child
nodes[i].right = &nodes[child];
else
nodes[i].right = NULL;
}
unvisited.push(&nodes[0]); //先把0放入UNVISITED stack
// 树的深度优先搜索在二叉树的特例下,就是二叉树的先序遍历操作(这里是使用循环实现)
// 只有UNVISITED不空
while (!unvisited.empty()) {
current = (unvisited.top()); //当前访问的
unvisited.pop();
if (current->right != NULL)
unvisited.push(current->right );
if (current->left != NULL)
unvisited.push(current->left);
cout << current->self << endl;
}
参考文献
- [算法导论]. ISBN 978-7-111-40701-0.
- . [2017-10-29]. (原始内容存档于2017-10-30) (英语).
參見
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.