热力学循环

热机图

热机循环是热机工作的基本原理，这种循环方式为当前世界上大部分的发电站提供能量来源，也为几乎所有的机动车提供动力。热机循环按照它们所采用的热机模型可进一步分类，内燃机中最常见的热机循环是奥托循环（常称做四冲程循环），柴油机中最常见的是迪塞尔循环。外燃机中使用的循环方式还包括采用燃气轮机方式工作的布雷顿循环，以及采用汽轮机方式工作的兰金循环。

箭头指向顺时针方向的热力学循环表示这是一个热机循环。循环由四个热力学态（四个打叉的点）和四个热力学过程（四条线段）构成。

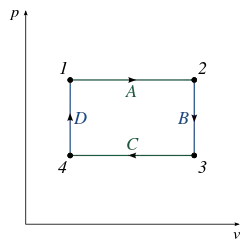
这里在P－V图上举例说明如何计算一个由四个热力学过程构成的热机循环所做的机械功：

${\displaystyle {\text{(3)}}\qquad W=W_{1\to 2}+W_{2\to 3}+W_{3\to 4}+W_{4\to 1}}$

${\displaystyle W_{1\to 2}=\int _{V_{1}}^{V_{2}}P\,dV,\,\,}$ 系统做正功

${\displaystyle W_{2\to 3}=\int _{V_{2}}^{V_{3}}P\,dV,\,\,}$ 当${\displaystyle V_{2}=V_{3}\,}$时系统不做功

${\displaystyle W_{3\to 4}=\int _{V_{3}}^{V_{4}}P\,dV,\,\,}$ 系统做负功

${\displaystyle W_{4\to 1}=\int _{V_{4}}^{V_{1}}P\,dV,\,\,}$ 当${\displaystyle V_{4}=V_{1}\,}$时系统不做功

在过程4->1以及2->3中，如果体积没有变化，则方程（3）简化为

${\displaystyle {\text{(4)}}\qquad W=W_{1\to 2}+W_{3\to 4}}$

热泵循环和制冷循环是热泵和冰箱的理论模型。两者的差别在于热泵的用途是保持一块区域的温度而冰箱则是使之降温。最常见的制冷循环是采用制冷剂的相变进行的蒸气压缩循环。吸收制冷循环是另一种循环方式，它不将制冷剂气化，而是将其吸收。气体制冷循环包括逆向布雷顿循环和林德－汉普逊循环。

卡诺循环由完全可逆的等熵压缩和膨胀过程，以及伴随有吸热和放热的等温过程组成。卡诺循环的热机效率只依赖于发生热传递的两个热库的热力学温度，对于一个循环周期，卡诺热机的效率为

${\displaystyle \eta =1-{\frac {T_{L}}{T_{H}}}}$

其中${\displaystyle {T_{L}}}$是循环过程中的最低温度（低温热库的温度），${\displaystyle {T_{H}}}$是最高温度（高温热库的温度）。对于卡诺制冷循环，热泵的性能系数为

${\displaystyle \ COP=1+{\frac {T_{L}}{T_{H}-T_{L}}}}$

对于一个制冷机，性能系数为

${\displaystyle \ COP={\frac {T_{L}}{T_{H}-T_{L}}}}$

热力学第二定律指出，任何热力学循环设备的效率和性能系数都不可能高于卡诺循环的效率。

一个理想热机的循环示意图（箭头指向顺时针方向）

一个理想热机的循环由下面过程组成：

1. 循环路径的上边和下边：平行的等压过程
2. 循环路径的左边和右边：平行的等容过程

一个奥托循环由下面过程组成：

1. 循环路径的上边和下边：一对准平行的绝热过程
2. 循环路径的左边和右边：一对平行的等容过程

斯特灵循环和奥托循环相似，但绝热过程被替换为等温过程：

1. 循环路径的上边和下边：一对准平行的等温过程
2. 循环路径的左边和右边：一对平行的等容过程