膠子
在粒子物理學中,膠子(gluon)是負責在兩個夸克之間傳遞強作用力的基本粒子,類似光子負責在兩個帶電粒子之間傳遞電磁力一般。[5]
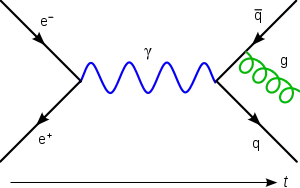 電子與正子湮滅的費曼圖,膠子通常是以螺旋線表示。 | |
| 组成 | 基本粒子 |
|---|---|
| 系 | 玻色 |
| 基本相互作用 | 強相互作用 |
| 符号 | g |
| 理论 | 默里·蓋爾曼(1962年)[1] |
| 发现 | 吴秀兰團隊(1979年)[2] |
| 类型 | 8 |
| 质量 | 0 MeV (理論值)[3] < 0.0002 eV (實驗上限)[4] |
| 電荷 | 0 e[3] |
| 色荷 | 8個線性獨立種類 |
| 自旋 | 1 |
用科學術語來說明,膠子是量子色動力學用來在兩個夸克之間傳遞強相互作用的矢量規範玻色子。膠子本身帶有強相互作用的色荷,這與光子不同,光子不帶有電荷。因此,膠子不但傳遞強相互作用,它還參與強相互作用,這使得量子色動力學的分析遠比量子電動力學困難。[6]:66-71
性質
膠子是矢量規範玻色子,如同光子,它的自旋為1。自旋為1的帶質量粒子可以擁有三種偏振態。在量子場論裏,為了滿足局域規範不變性,規範玻色子的質量必須為零,因此膠子不帶質量(實驗上限為0.0002 eV[4]),所以,只有兩種偏振態。[6]:239-241, 286
膠子的工作機制
在量子色動力學裏,依照所帶有的色荷與反色荷來區分,一共存在有8種不同的膠子。每個夸克都帶有三個不同的色荷:紅色、藍色與綠色。每個反夸克都帶有三個不同的反色荷:反紅色、反藍色與反綠色。每個膠子帶有一個色荷與一個反色荷。要想正確了解它們怎樣組合在一起,就必需更仔細地思考色荷數學。
色荷與量子疊加
在量子力學裏,根據態疊加原理,假若粒子處於由幾種量子態組合而成的疊加態,則粒子處於其中任意量子態的概率為有限值;假若對於這系統測量某物理量,則可能得到幾種不同的數值。[7]:316ff例如,設定膠子的色態為紅色-反藍色加上藍色-反紅色:
- ;
其中,、、、分別為紅色、藍色、反紅色、反藍色。
假若測量此膠子的顏色,則它的色荷是紅色-反藍色的機會為50%,是藍色-反紅色的機會為50% 。
色單態
在科普界時常會提到,由幾個夸克或反夸克組成的穩定粒子,例如像質子與中子一類的強子,假若能夠在大自然被觀察得到,則總色荷必須是無色的(或白色的):[6]:42-43
所有自然發生的粒子都是無色的。
更精準地說,所有自然發生的粒子都處於色單態,這是為了遵守夸克禁閉。例如,每一種重子的波函數在顏色部分必須是反對稱的色單態:[6]:186
- ;
其中,為綠色。
膠子的色單態為[6]:285
- 。
由於色單態的膠子不違反夸克禁閉,它應該能夠以自由粒子的形式存在於大自然,並且在兩個強子之間傳遞強作用力,例如,在質子與中子之間傳遞強作用力,因此,強作用力也會變為遠距作用力,但是強作用力是一種短距作用力,因此色單態的膠子不存在。
八種膠子
每個膠子帶有一個單位色荷的顏色與一個單位色荷的反顏色。顏色可以是紅色、藍色或綠色。反顏色可以是反紅色、反藍色或反綠色。所以,膠子可能處於九種不同的色態,分別為、、、、、、、、。實際而言,膠子是處於這九種色態的線性獨立組合,但是由於先前提到的色單態並不存在,所以只有八種色態,分別為[6]:285
| 。 |
這些色態共同組成「八重態」,或「色八重態」。這些色態的色波函數等價於蓋爾曼矩陣,分别为:
在蓋爾曼矩陣裏,第一橫排第二豎排的元素對應於紅色-反藍色,第二橫排第一豎排的元素對應於藍色-反紅色,整個矩陣對應於色態。
這八個色態彼此線性獨立,並且獨立於色單態;幾個色態的任何線性組合都無法複製其它色態;它也無法製成、、,否則,禁戒的色單態也可被製成。[8]
上述八重態並不是唯一選擇,也可挑選其它種八重態,但它們都數學等價,會給出同樣的物理結果,並且運算過程不會更簡易。
禁閉
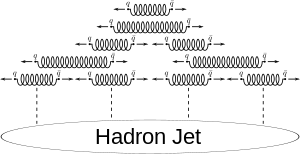
由於膠子本身帶有色荷,膠子也參與強相互作用。膠子-膠子相互作用使得色場成為像絲弦一般的物體,稱為「通量管」(flux tube)。[註 1]當通量管被拉長時,會出現張力,因此將夸克禁閉於強子內部,這機制有效地局限強作用力的範圍半徑至10−15 m以內,大約為原子核的尺寸。當超過某特定長度後,假若連結兩個夸克的通量管的長度越長,則能量越高,呈線性增長;當通量管被拉到足夠長之時,在能量方面,從真空製成一個夸克-反夸克對會比一味地增加通量管長度更為有利,這時,繼續拉長通量管還可能會導致通量管會斷裂,形成一個夸克-反夸克對。[9]:2324
雖然在量子色動力學的正常相,單獨膠子無法自由移動,物理學者猜測,可能存在純粹由膠子形成的強子,稱為膠球。[10]其它種奇異強子也可能存在,這些奇異強子的重要成分將會是真實膠子,而不是虛膠子。當不處於正常相之時,即在極端高溫與極端高壓強狀況,會形成夸克-膠子等離子體,在這夸克-膠子等離子體裏,不會有機會形成強子,因為夸克與膠子都會變成自由粒子。[11]
實驗觀察
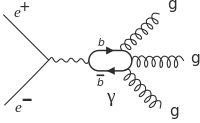
夸克與膠子藉著分裂成更多夸克與膠子來顯現自己。這些分裂出的夸克與膠子又會強子化成為無色的正常粒子。1978年夏季,在國際會議、座談會、專題研討會等等多個學術場合裏,[12]德國電子加速器的正負電子對撞機與儲存環(DORIS)的PLUTO 實驗團隊報告,發現非常狹窄共振Y(9.46)的強子型衰變可以詮釋為由三個膠子製成的 三重噴流事件的證據。同一團隊後來發表分析報告確定這詮釋正確無誤,並且展示出膠子的自旋為1。[13][14][12][15]
1979年夏季,在德國電子加速器的正負電子對撞機PETRA,TASSO實驗團隊、[16] MARK-J實驗團隊、[17] PLUTO實驗團隊[18](後來,在1980年,JADE粒子探測器[19]))又觀察到三重噴流事件,這被詮釋為qq膠子軔致輻射,現在更為明顯可見。 1980年,TASSO實驗團隊[20]與PLUTO實驗團隊[21]確定膠子的自旋為1。[2]1991年,在歐洲核子研究組織大型正負電子對撞機儲存環完成的一項後續實驗確定這結果正確無誤[22]
在德國電子加速器的強子-電子環加速器,膠子的物理性質被特別地研究分析。H1探測器實驗與ZEUS探測器實驗,這兩項實驗對於膠子在質子裏的數量分佈與動量分佈做出仔細測量。[23]從1996年至2007年,HERMES實驗研究膠子對於質子自旋的貢獻。從H1探測器實驗蒐集的光子製備數據,被用來計算光子內部的膠子密度,當光子呈現強子行為之時。[24]
色禁閉可以用無法找到自由夸克來核對,也就是說無法找到非整數的電荷。通常,為了抵銷量子顏色與風味量子數,夸克會成對產生(夸克與反夸克)。可是,在費米實驗室的CDF實驗團隊與D0實驗團隊於2009年報告,探測到頂夸克單獨產生的證據(雖然這仍舊涉及到成對產生,但是夸克與反夸克的風味不同)。[25]至今為止,尚未能找到任何膠球存在的證據。
2000年,歐洲核子研究組織的超級質子同步加速器聲稱,在重離子對撞時觀察到退禁閉,[26]這意味著觀察到一種新的物質態:夸克-膠子等離子體。2004年至2010年,在布魯克黑文國家實驗室的 相對論性重離子對撞機(RHIC),四個不同實驗同時期找到夸克-膠子等離子體。[27]2010年,在歐洲核子研究組織的大型強子對撞機,三個實驗大型離子對撞機實驗、超環面儀器與緊湊緲子線圈確定探測到夸克-膠子等離子體。[28]
参阅
- 夸克模型
註釋
- 由於膠子帶有色荷,幾個膠子會相互耦合,如右圖所示。光子不帶有電荷,所以不會相互耦合。
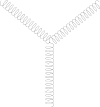 三個膠子相互作用
三個膠子相互作用 四個膠子相互作用
四個膠子相互作用
参考文献
- M. Gell-Mann. . Physical Review. 1962, 125 (3): 1067–1084. Bibcode:1962PhRv..125.1067G. doi:10.1103/PhysRev.125.1067.
- P. Söding. . European Physical Journal H. 2010, 35 (1): 3–28. Bibcode:2010EPJH...35....3S. doi:10.1140/epjh/e2010-00002-5.
- W.-M. Yao; et al. (PDF). Journal of Physics G. 2006, 33: 1 [2008-01-25]. Bibcode:2006JPhG...33....1Y. arXiv:astro-ph/0601168
 . doi:10.1088/0954-3899/33/1/001. (原始内容存档 (PDF)于2017-02-22).
. doi:10.1088/0954-3899/33/1/001. (原始内容存档 (PDF)于2017-02-22). - F. Yndurain. . Physics Letters B. 1995, 345 (4): 524. Bibcode:1995PhLB..345..524Y. doi:10.1016/0370-2693(94)01677-5.
- C.R. Nave. . HyperPhysics. Georgia State University, Department of Physics. [2012-04-02]. (原始内容存档于2007-08-20).
- Griffiths, David J., 2nd revised, WILEY-VCH, 2008, ISBN 978-3-527-40601-2
- French, Anthony, , W. W. Norton, Inc., 1978, ISBN 0-393-09106-0 请检查
|isbn=值 (帮助) - J. Baez. . [2009-09-13]. (原始内容存档于2001-11-01).
- Jeff Greensite. . Springer Science & Business Media. 23 January 2011. ISBN 978-3-642-14381-6.
- Frank Close and Phillip R. Page, "Glueballs", Scientific American, vol. 279 no. 5 (November 1998) pp. 80–85
- Miklos Gyulassy. . 2004. arXiv:nucl-th/0403032

|class=被忽略 (帮助). -
B.R. Stella and H.-J. Meyer. . European Physical Journal H. 2011, 36 (2): 203–243. Bibcode:2011EPJH...36..203S. arXiv:1008.1869v3
 . doi:10.1140/epjh/e2011-10029-3.
. doi:10.1140/epjh/e2011-10029-3. - Ch. Berger et al. (PLUTO Collaboration). . Physics Letters B. 1979, 82 (3–4): 449. Bibcode:1979PhLB...82..449B. doi:10.1016/0370-2693(79)90265-X.
- Ch. Berger et al. (PLUTO Collaboration). . Zeitschrift für Physik C. 1981, 8 (2): 101. Bibcode:1981ZPhyC...8..101B. doi:10.1007/BF01547873.
- A. Ali and G. Kramer. . European Physical Journal H. 2011, 36 (2): 245–326. Bibcode:2011EPJH...36..245A. arXiv:1012.2288
 . doi:10.1140/epjh/e2011-10047-1.
. doi:10.1140/epjh/e2011-10047-1. - R. Brandelik et al. (TASSO collaboration). . Physics Letters B. 1979, 86 (2): 243–249. Bibcode:1979PhLB...86..243B. doi:10.1016/0370-2693(79)90830-X.
- D.P. Barber et al. (MARK-J collaboration). . Physical Review Letters. 1979, 43 (12): 830. Bibcode:1979PhRvL..43..830B. doi:10.1103/PhysRevLett.43.830.
- Ch. Berger et al. (PLUTO Collaboration). . Physics Letters B. 1979, 86 (3–4): 418. Bibcode:1979PhLB...86..418B. doi:10.1016/0370-2693(79)90869-4.
- W. Bartel et al. (JADE Collaboration). . Physics Letters B. 1980, 91: 142. Bibcode:1980PhLB...91..142B. doi:10.1016/0370-2693(80)90680-2.
- R. Brandelik et al. (TASSO Collaboration). . Physics Letters B. 1980, 97 (3–4): 453. Bibcode:1980PhLB...97..453B. doi:10.1016/0370-2693(80)90639-5.
- Ch. Berger et al. (PLUTO Collaboration). . Physics Letters B. 1980, 97 (3–4): 459. Bibcode:1980PhLB...97..459B. doi:10.1016/0370-2693(80)90640-1.
- G. Alexander et al. (OPAL Collaboration). . Zeitschrift für Physik C. 1991, 52 (4): 543. Bibcode:1991ZPhyC..52..543A. doi:10.1007/BF01562326.
- L. Lindeman (H1 and ZEUS collaborations). . Nuclear Physics B Proceedings Supplements. 1997, 64: 179–183. Bibcode:1998NuPhS..64..179L. doi:10.1016/S0920-5632(97)01057-8.
-
C. Adloff et al. (H1 collaboration). . European Physical Journal C. 1999, 10: 363–372. Bibcode:1999EPJC...10..363H. arXiv:hep-ex/9810020
 . doi:10.1007/s100520050761.
. doi:10.1007/s100520050761. - M. Chalmers. . Physics World. 6 March 2009 [2012-04-02]. (原始内容存档于2012-02-09).
- M.C. Abreu; et al. . Physics Letters B. 2000, 477: 28–36. Bibcode:2000PhLB..477...28A. doi:10.1016/S0370-2693(00)00237-9.
- D. Overbye. . New York Times. 15 February 2010 [2012-04-02]. (原始内容存档于2021-05-08).
- (新闻稿). CERN. 26 November 2010 [2012-04-02]. (原始内容存档于2012年3月13日).