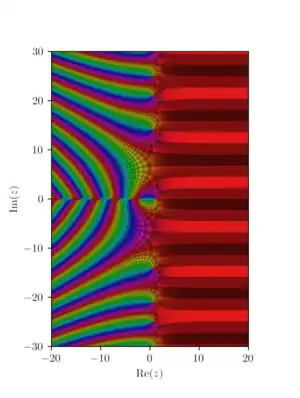
黎曼ζ函數

黎曼泽塔函數 ，写作 $ζ(s)$ 的定義如下：設一複數 $s$ 使得 $Re(s) > 1$ ，則定義：

\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}

複平面中一矩形區域之黎曼ζ函數

\zeta (z)

；此圖用Matplotlib程式繪圖產生，使用到定義域著色方法。[1]

它亦可以用积分定义：

\zeta (s)={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{\frac {x^{s-1}}{e^{x}-1}}\mathrm {d} x

在区域 { $s : Re(s) > 1}$ 上，此无穷级数收敛并为一全纯函数。欧拉在1740年考虑过 $s$ 为正整数的情况，后来切比雪夫拓展到 $s > 1$ 。[2]波恩哈德·黎曼认识到：ζ函数可以通过解析延拓，把定義域扩展到幾乎整個复数域上的全纯函数 $ζ(s)$ 。这也是黎曼猜想所研究的函数。

虽然黎曼的ζ函数被数学家认为主要和“最纯”的数学领域数论相关，它也出现在应用统计学（参看齊夫定律和齊夫-曼德爾布羅特定律）、物理，以及调音的数学理论中。

历史

奥里斯姆

ζ函数最早出现于1350年左右，尼克尔·奥里斯姆发现了调和级数发散，即： $\zeta (1)=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+...\to \infty$

奥里斯姆对调和级数发散的“证明”

{\begin{aligned}\zeta (1)&=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+...\\&=1+{\frac {1}{2}}+({\frac {1}{3}}+{\frac {1}{4}})+({\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}})+...\\&\geq 1+{\frac {1}{2}}+({\frac {1}{4}}+{\frac {1}{4}})+({\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}})+...\\&=1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+...\\&\to \infty \\\end{aligned}}

欧拉

第n个调和数（蓝点）与Log(n)+γ(红线)的图像

之后的一次进展来自莱昂哈德·欧拉，他给出了调和级数呈对数发散。

欧拉对调和级数发散速度的证明[3]

为了求出调和级数的部分和，使用欧拉-麦克劳林求和公式（当然，亦可使用阿贝尔求和公式）：

$\sum _{y<n\leq x}f(n)=\int _{y}^{x}f(t)\,\mathrm {d} t+\int _{y}^{x}(t-\left\lfloor t\right\rfloor )f'(t)\,\mathrm {d} t+f(x)(\left\lfloor x\right\rfloor -x)-f(y)(\left\lfloor y\right\rfloor -y)$ ${\begin{aligned}\sum _{n\leq x}{\frac {1}{n}}&=1+\int _{1}^{x}{\frac {1}{t}}\,\mathrm {d} t-\int _{1}^{x}{\frac {(t-\left\lfloor t\right\rfloor )}{t^{2}}}\,\mathrm {d} t+{\frac {\left\lfloor x\right\rfloor -x}{x}}\\&=1+\ln x-\int _{1}^{x}{\frac {(t-\left\lfloor t\right\rfloor )}{t^{2}}}\,\mathrm {d} t+\mathrm {O} \left({\frac {1}{x}}\right)\\&=1+\ln x-\int _{1}^{\infty }{\frac {(t-\left\lfloor t\right\rfloor )}{t^{2}}}\,\mathrm {d} t+\int _{x}^{\infty }{\frac {(t-\left\lfloor t\right\rfloor )}{t^{2}}}\,\mathrm {d} t+\mathrm {O} \left({\frac {1}{x}}\right)\\&=\ln x+1-\int _{1}^{\infty }{\frac {(t-\left\lfloor t\right\rfloor )}{t^{2}}}\,\mathrm {d} t+\int _{x}^{\infty }{\frac {\left\{t\right\}}{t^{2}}}\,\mathrm {d} t+\mathrm {O} \left({\frac {1}{x}}\right)\\\end{aligned}}$
注意到其中的
$1-\int _{1}^{\infty }{\frac {(t-\left\lfloor t\right\rfloor )}{t^{2}}}\,\mathrm {d} t$ 是一个常数。实际上，这就是歐拉-馬斯刻若尼常數γ 再考虑剩下的一个积分，也就是 $\int _{x}^{\infty }{\frac {\left\{t\right\}}{t^{2}}}\,\mathrm {d} t$
由于被积项非负，又有 $\left\{t\right\}\leq 1$ ，于是
$\int _{x}^{\infty }{\frac {\left\{t\right\}}{t^{2}}}\,\mathrm {d} t\leq \int _{x}^{\infty }{\frac {1}{t^{2}}}\,\mathrm {d} t={\frac {1}{x}}$ 最终得到
$\sum _{n\leq x}{\frac {1}{n}}=\ln x+\gamma +\mathrm {O} ({\frac {1}{x}})$

除此之外，他还在1735年给出了巴塞尔问题的解答，得到
$\zeta (2)={\frac {\pi ^{2}}{6}}$
的结果。欧拉最初的证明可以在巴塞尔问题#欧拉的錯誤證明中看到，然而那是他的第一个证明，因而广为人知。
事实上，那个证明虽有不严谨之处，但是欧拉仍然有自己的严格证明。[4]

欧拉对

{\begin{smallmatrix}\zeta (2)={\frac {\pi ^{2}}{6}}\end{smallmatrix}}

的严格证明

下面将写出欧拉对上式的证明中缺失的严格论证的部分，即对连乘积公式的证明部分，而不涉及最终的系数比较

首先考虑当n为奇数时，将 $z^{n}-a^{n}$ 分解为连乘积形式。事实上，容易发现上式的全部复根为 $a,ae^{2\pi i{\frac {1}{n}}},ae^{2\pi i{\frac {2}{n}}},...,ae^{2\pi i{\frac {n-1}{n}}}$

由于n为奇数，所以可以将除了z=a外的其他根及其共轭一一配对，即

将共轭的根一一配对

$ae^{2\pi i{\frac {k}{n}}},ae^{2\pi i{\frac {n-k}{n}}}=ae^{-2\pi i{\frac {k}{n}}}$ 看做一对，
则通过二次方程的韦达定理可以还原出每对根的最小多项式：
按照韦达定理，有
$x_{1}+x_{2}=-{\frac {a_{1}}{a_{0}}}=ae^{2\pi i{\frac {k}{n}}}+ae^{-2\pi i{\frac {k}{n}}}=\cos \left(2\pi {\frac {k}{n}}\right)+\cos \left(-2\pi {\frac {k}{n}}\right)=2\cos \left({\frac {2\pi k}{n}}\right)$
$x_{1}x_{2}={\frac {a_{2}}{a_{0}}}=ae^{2\pi i{\frac {k}{n}}}ae^{-2\pi i{\frac {k}{n}}}=a^{2}$
由于最小多项式首项系数为1，故 $a_{0}=1$ ，由此得到这对根最小多项式为
$a_{0}z^{2}+a_{1}z+a_{2}=z^{2}-2\cos \left({\tfrac {2\pi k}{n}}\right)z+a^{2}$ 注意到k的取值上限为 ${\tfrac {n-1}{2}}$ ，将每一对根的最小多项式相乘，
还有z=a这个根的最小多项式 $z-a$ ，乘在一起，得到
$z^{n}-a^{n}=(z-a)\prod _{k=1}^{\frac {n-1}{2}}\left(z^{2}-2az\cos {\frac {2k\pi }{n}}+a^{2}\right)$

令 $z=1+{\frac {x}{N}},a=1-{\frac {x}{N}},N=n$ ，代入上式，有：
${\begin{aligned}\left(1+{\frac {x}{N}}\right)^{N}-\left(1-{\frac {x}{N}}\right)^{N}&=\left[\left(1+{\frac {x}{N}}\right)-\left(1-{\frac {x}{N}}\right)\right]\prod _{k=1}^{\frac {N-1}{2}}\left[\left(1+{\frac {x}{N}}\right)^{2}-2\left(1+{\frac {x}{N}}\right)\left(1-{\frac {x}{N}}\right)\cos \left({\frac {2\pi k}{N}}\right)+\left(1-{\frac {x}{N}}\right)^{2}\right]\\&={\frac {2x}{N}}\prod _{k=1}^{\frac {N-1}{2}}\left[2+{\frac {2x^{2}}{N^{2}}}-2\left(1-{\frac {x^{2}}{N^{2}}}\right)\cos \left({\frac {2\pi k}{N}}\right)\right]\\&={\frac {2x}{N}}\prod _{k=1}^{\frac {N-1}{2}}\left[{2+{\frac {2{x^{2}}}{N^{2}}}-2\cos \left({\frac {2\pi k}{N}}\right)+{\frac {2{x^{2}}}{N^{2}}}\cos({\frac {2\pi k}{N}})}\right]\\&={\frac {4x}{N}}\prod _{k=1}^{\frac {N-1}{2}}\left({(1-\cos({\frac {2\pi k}{N}}))+(1+\cos({\frac {2\pi k}{N}})){\frac {x^{2}}{N^{2}}}}\right)\\&={\frac {4x}{N}}\prod _{k=1}^{\frac {N-1}{2}}\left\{\left[1-\cos \left({\frac {2\pi k}{N}}\right)\right]\left[{1+{\frac {1+\cos \left({\frac {2\pi k}{N}}\right)}{1-\cos({\frac {2\pi k}{N}})}}{\frac {x^{2}}{N^{2}}}}\right]\right\}\\\end{aligned}}$

此时，上述乘积中的 ${\frac {4}{N}}\prod _{k=1}^{\frac {N-1}{2}}(1-\cos({\frac {2\pi k}{N}}))$ 仅和N有关，记作 $C(N)$ ，上式变为
$\left(1+{\frac {x}{N}}\right)^{N}-\left(1-{\frac {x}{N}}\right)^{N}={C(N)}x\prod _{k=1}^{\frac {N-1}{2}}\left({1+{\frac {1+\cos({\frac {2\pi k}{N}})}{1-\cos({\frac {2\pi k}{N}})}}{\frac {x^{2}}{N^{2}}}}\right)$
而利用二项式定理，将等式左边展开：
${(1+{\frac {x}{N}})^{N}}=\sum _{k=0}^{N}{C_{N}^{k}{\frac {x^{k}}{N^{k}}}}$
${(1-{\frac {x}{N}})^{N}}=\sum _{k=0}^{N}{{{(-1)}^{k}}C_{N}^{k}{\frac {x^{k}}{N^{k}}}}$
两式相减，考虑一次项，为 $C_{N}^{1}{\frac {x}{N}}-(-1)C_{N}^{1}{\frac {x}{N}}=2C_{N}^{1}{\frac {x}{N}}=2x$
这正是等式的左边的一次项
而等式右边的一次项只能是连乘积中的全部1与连乘积外的C(n)x相乘，为使两边相等，必须有 $C(N)=2$ ，于是上式变为
$\left(1+{\frac {x}{N}}\right)^{N}-\left(1-{\frac {x}{N}}\right)^{N}=2x\prod _{k=1}^{\frac {N-1}{2}}\left({1+{\frac {1+\cos({\frac {2\pi k}{N}})}{1-\cos({\frac {2\pi k}{N}})}}{\frac {x^{2}}{N^{2}}}}\right)$

另一方面，令 $\theta ={\frac {2\pi k}{N}}$ ，有
$\cos(\theta )=1-{\frac {\theta ^{2}}{2}}+\mathrm {O} (\theta ^{3})$ 于是，代入上式，得到
${\begin{aligned}\left(1+{\frac {x}{N}}\right)^{N}-\left(1-{\frac {x}{N}}\right)^{N}&=2x\prod _{k=1}^{\frac {N-1}{2}}\left[1+{\frac {1+\cos \left({\frac {2\pi k}{N}}\right)}{1-\cos \left({\frac {2\pi k}{N}}\right)}}{\frac {x^{2}}{N^{2}}}\right]\\&=2x\prod _{k=1}^{\frac {N-1}{2}}\left\{1+{\frac {1+\left[1-{\frac {\theta ^{2}}{2}}+\mathrm {O} \left(\theta ^{3}\right)\right]}{1-\left[1-{\frac {\theta ^{2}}{2}}+\mathrm {O} \left(\theta ^{3}\right)\right]}}{\frac {x^{2}}{N^{2}}}\right\}\\&=2x\prod _{k=1}^{\frac {N-1}{2}}\left[1+{\frac {2-{\frac {\theta ^{2}}{2}}+\mathrm {O} \left(\theta ^{3}\right)}{{\frac {\theta ^{2}}{2}}+\mathrm {O} \left(\theta ^{3}\right)}}{\frac {x^{2}}{N^{2}}}\right]\\&=2x\prod _{k=1}^{\frac {N-1}{2}}\left(1+{\frac {\left(4-\theta ^{2}+\mathrm {O} \left(\theta ^{3}\right)\right)x^{2}}{\left(\theta ^{2}+\mathrm {O} \left(\theta ^{3}\right)\right)N^{2}}}\right)\\&=2x\prod _{k=1}^{\frac {N-1}{2}}\left(1+{\frac {\left(4-\left({\frac {2k\pi }{N}}\right)^{2}+\mathrm {O} \left(\left({\frac {2k\pi }{N}}\right)^{3}\right)\right)x^{2}}{\left(\left({\frac {2k\pi }{N}}\right)^{2}+\mathrm {O} \left(\left({\frac {2k\pi }{N}}\right)^{3}\right)\right)N^{2}}}\right)\\&=2x\prod _{k=1}^{\frac {N-1}{2}}\left(1+{\frac {\left(4-\left({\frac {2k\pi }{N}}\right)^{2}+\mathrm {O} \left(\left({\frac {2k\pi }{N}}\right)^{3}\right)\right)x^{2}}{(2k\pi )^{2}+\mathrm {O} \left({\frac {(2k\pi )^{3}}{N}}\right)}}\right)\end{aligned}}$

令N→∞，则右端大O符号的诸项都变为无穷小。另一方面，左端可写为：
$\lim _{N\to \infty }(1+{\frac {x}{N}})^{N}-(1-{\frac {x}{N}})^{N}=e^{x}-e^{-x}$
于是上式变为
${\begin{aligned}e^{x}-e^{-x}&=2x\prod _{k=1}^{\infty }\left({1+{\frac {(4+o(1)){x^{2}}}{{{(2k\pi )}^{2}}+o(1)}}}\right)\ \\&=2x\prod _{k=1}^{\infty }\left({1+{\frac {(1+o(1)){x^{2}}}{{k^{2}}{\pi ^{2}}+o(1)}}}\right)\ \\&=2x\prod _{k=1}^{\infty }\left({1+{\frac {x^{2}}{{k^{2}}{\pi ^{2}}}}}\right)\ \\\end{aligned}}$
此时，只需比较左右两端展开式的三次项系数，即可得出结果。
对左式进行级数展开，可得： $e^{x}-e^{-x}=-\sum _{k=0}^{\infty }{\frac {(-x)^{k}-x^{k}}{k!}}$
其中当 $k=3$ 时可提取左式的三次项为 ${\frac {2x^{3}}{3!}}$ 。

同时展开右式可得右式的三次项为 $\left(\sum _{k=1}^{\infty }{\frac {2}{k^{2}\pi ^{2}}}\right)x^{3}$
由于等式左右端相等，所以左右式三次项系数必须相等, 因此可得： ${\frac {2}{3!}}=\sum _{k=1}^{\infty }{\frac {2}{k^{2}\pi ^{2}}}$
化简可得： ${\frac {\pi ^{2}}{6}}=\sum _{k=1}^{\infty }{\frac {1}{k^{2}}}=\zeta \left(2\right)$

欧拉在1737年还发现了欧拉乘积公式：
$\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=\prod _{p}(1-{\frac {1}{p^{s}}})^{-1}$
这是ζ函数与素数的联系的朦胧征兆，其证明可以在证明黎曼ζ函数的欧拉乘积公式中看到。
通过这条公式，容易证明当 ${\begin{smallmatrix}\operatorname {Re} (s)>1\end{smallmatrix}}$ 时， ${\begin{smallmatrix}\zeta (s)>0\end{smallmatrix}}$

1749年，欧拉通过大胆的计算發現了(以下公式當中存在定義域謬誤，後由黎曼透過解析延拓証明以下公式只適用於 $Re(s) > 1$ )[5]
$\zeta (-1)=1+2+3+4+5+...=-{\frac {1}{12}}$
$\zeta (-2)=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+...=0$
$\zeta (-3)=1^{3}+2^{3}+3^{3}+4^{3}+5^{3}+...={\frac {1}{120}}$
发现ζ(s)与ζ(1-s)之间存在某些关系。

黎曼

波恩哈德·黎曼对ζ解析延拓，用于素数的分布理论

将欧拉所做的一切牢牢地置于坚石之上的是黎曼，他在1859年的论文论小于给定数值的素数个数以及未发表的手稿中做出了多项进展：[6]

第一积分表示： $\zeta (s)={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{\frac {x^{s-1}}{e^{x}-1}}\,\mathrm {d} x$
完备化的ζ，即黎曼ξ函数： $\xi (s)=\pi ^{-{\frac {s}{2}}}\Gamma \left({\frac {s}{2}}\right)\zeta (s)$ ，满足函数方程 $\xi (s)=\xi (1-s)$
第二积分表示： $\varphi (x)=\sum _{n=1}^{\infty }e^{-\pi n^{2}x}$ ，则 $\xi (s)=\int _{0}^{\infty }\varphi (x)x^{{\frac {s}{2}}-1}\,\mathrm {d} x$
黎曼 - 冯·曼戈尔特公式：以 ${\begin{smallmatrix}0<\operatorname {N} (T)\end{smallmatrix}}$ 表示虚部介于0与T之间的非平凡零点数量，则 $N(T)={\frac {T}{2\pi }}\log {\frac {T}{2\pi }}-{\frac {T}{2\pi }}+\mathrm {O} (\log T)$
黎曼猜想：ζ函数的所有非平凡零点的实部非常有可能均为 ${\begin{smallmatrix}{\frac {1}{2}}\end{smallmatrix}}$

第三积分表示： $\zeta (s)={\frac {1}{2\pi i}}\Gamma (1-s)\oint _{\gamma }{\frac {{z^{s-1}}{e^{z}}}{1-{e^{z}}}}\,\mathrm {d} z$ ，其中围道γ逆时针环绕负实轴

第三积分表示的围道γ

黎曼-西格尔公式：给出计算ξ函数的数值的方法
零点的计算：计算了虚部介于0与100的所有零点的数值
素数的分布公式：引入黎曼素数计数函数，给出了它与ζ函数的关系

阿达马与普森

ζ(1+it)的图像，蓝色为实部，黄色为虚部

1896年，雅克·阿达马与普森几乎同时地证明了 ${\begin{smallmatrix}\zeta (s)\end{smallmatrix}}$ 的所有非平凡零点的实部均小于1，即 ${\begin{smallmatrix}\operatorname {Re} (s)=1\end{smallmatrix}}$ 上无非平凡零点，从而完成了素数定理的证明。

希尔伯特

1900年，希尔伯特在巴黎的第二届国际数学家大会上作了题为《数学问题》的演讲，提出了23道最重要的数学问题，黎曼假设在其中作为第8题出现。
之后，希尔伯特提出了希尔伯特－波利亚猜想，具体时间及场合未知。

玻尔与兰道

虚部介于0与T的零点数量（蓝点）与黎曼-冯·曼格尔特公式（红线）的图像

1914年，哈那德·玻爾和愛德蒙·蘭道证明了玻爾-蘭道定理：含有临界线的任意带状区域都几乎包含了ζ的所有非平凡零点，表明了临界线为零点汇聚的“中心位置”。

哈代与李特尔伍德

1921年，哈代和李特尔伍德证明了存在常数T，使临界线上虚部位于0与T之间的非平凡零点的数量至少为 ${\begin{smallmatrix}KT\end{smallmatrix}}$ 。

塞尔伯格

1942年，阿特勒·塞尔伯格更进一步，证明了存在常数T，使临界线上虚部位于0与T之间的非平凡零点的数量至少为 ${\begin{smallmatrix}KT\log T\end{smallmatrix}}$ ，这意味着ζ函数在临界线上的非平凡零点在所有零点中占有一个正密度，而临界线 ${\begin{smallmatrix}\operatorname {Re} (s)={\frac {1}{2}}\end{smallmatrix}}$ 对于临界带 ${\begin{smallmatrix}0<\operatorname {Re} (s)<1\end{smallmatrix}}$ 的测度为0。

解析延拓

对ζ函数解析延拓时使用的围道

ζ函数原本定义在右半平面 ${\begin{smallmatrix}\operatorname {Re} s>1\end{smallmatrix}}$ 上，并且在此区域内为全纯函数

\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{\frac {x^{s-1}}{e^{x}-1}}\,\mathrm {d} x

(\operatorname {Re} s>1)

解析延拓后在全局具有积分表达式

\zeta (s)={\frac {1}{2\pi i}}\Gamma (1-s)\oint _{\gamma }{\frac {{z^{s-1}}{e^{z}}}{1-{e^{z}}}}\,\mathrm {d} z

满足函数方程

\zeta (1-s)=2(2\pi )^{-s}\Gamma (s)\cos \left({\frac {\pi s}{2}}\right)\zeta (s)

特别地，如果考虑正规化的ζ，即黎曼ξ函数

\xi (s)=\pi ^{-{\frac {s}{2}}}\Gamma \left({\frac {s}{2}}\right)\zeta (s)

那么它满足函数方程

\xi (s)=\xi (1-s)

和数论函数的关系

黎曼ζ函数可看做是具有如下形式的级数的一个特例：

\operatorname {F} (s)=\sum _{n=1}^{\infty }{\frac {f(n)}{n^{s}}}

这种类型的级数被称作狄利克雷级数。当f为狄利克雷特征时，又称作狄利克雷L函数，也有与黎曼猜想相应的广义黎曼猜想

为了方便对数论函数作讨论，此处引入狄利克雷卷积 ${\begin{smallmatrix}f*g\end{smallmatrix}}$ ：
$(f*g)(n)=\sum _{{\text{pq}}=n}f(p)g(q)$

设 $\operatorname {F} (s)=\sum _{n=1}^{\infty }{\frac {f(n)}{n^{s}}}$ ， $\operatorname {G} (s)=\sum _{n=1}^{\infty }{\frac {g(n)}{n^{s}}}$
于是显然 $\operatorname {F} (s)\operatorname {G} (s)=\sum _{n=1}^{\infty }{\frac {(f*g)(n)}{n^{s}}}$

並不直覺？请看证明

事实上，

${\begin{aligned}\operatorname {F} (s)\operatorname {G} (s)&=\sum _{n=1}^{\infty }{\frac {f(n)}{n^{s}}}\sum _{m=1}^{\infty }{\frac {g(m)}{m^{s}}}\\&=\sum _{n=1}^{\infty }\sum _{m=1}^{\infty }{\frac {f(n)g(m)}{(nm)^{s}}}\\\end{aligned}}$

为了处理两个求和号，将所有可能的m与n的积相同的项合并，不妨设mn=k，那么
${\begin{aligned}\sum _{m=1}^{\infty }{\frac {f(n)g(m)}{(nm)^{s}}}&=\sum _{k=1}^{\infty }\sum _{{\text{mn}}=k}{\frac {f(m)g(n)}{(mn)^{s}}}\\&=\sum _{k=1}^{\infty }\sum _{{\text{mn}}=k}{\frac {f(m)g(n)}{k^{s}}}\\&=\sum _{k=1}^{\infty }(\sum _{{\text{mn}}=k}f(m)g(n))k^{-s}\\&=\sum _{k=1}^{\infty }(f*g)(k)k^{-s}\\\end{aligned}}$

于是，如果数论函数 ${\begin{smallmatrix}h=1*g\end{smallmatrix}}$ ，亦即 $h(n)=\sum _{d\|n}g(d)$ (此时， ${\begin{smallmatrix}h(n)\end{smallmatrix}}$ 与 ${\begin{smallmatrix}g(d)\end{smallmatrix}}$ 可通过默比乌斯反演公式相互转换)
那么 $\operatorname {H} (s)=\sum _{n=1}^{\infty }{\frac {h(n)}{n^{s}}}=\zeta (s)\sum _{n=1}^{\infty }{\frac {g(n)}{n^{s}}}$
通常两侧的求和有一个是相对简单的函数，或是和 ${\begin{smallmatrix}\zeta (s)\end{smallmatrix}}$ 直接相关的函数
如果对 ${\begin{smallmatrix}g(n)\end{smallmatrix}}$ 的求和较简单，可以将 ${\begin{smallmatrix}h(n)\end{smallmatrix}}$ 与 ${\begin{smallmatrix}\zeta (s)\end{smallmatrix}}$ 相联系，反之可以将 ${\begin{smallmatrix}g(n)\end{smallmatrix}}$ 与 ${\begin{smallmatrix}\zeta (s)\end{smallmatrix}}$ 相联系
即 $\sum _{n=1}^{\infty }{\frac {g(n)}{n^{s}}}={\frac {\operatorname {H} (s)}{\zeta (s)}}$ ，
如下表所示：

目标函数名	g(n)	h(n)	G(s)或H(s)	g(n)或h(n)与ζ函数的联系
莫比乌斯函数	$\mu (n)=\mu (p_{1}^{a_{1}}p_{2}^{a_{2}}...p_{k}^{a_{k}})={\begin{cases}(-1)^{k}&a_{1}=a_{2}=...=a_{k}\\0&\mathrm {otherwise} \end{cases}}$	$\left\lfloor {\frac {1}{n}}\right\rfloor$	$\operatorname {H} (s)=1$	$\operatorname {G} (s)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n^{s}}}={\frac {1}{\zeta (s)}}$
欧拉函数	$\varphi (n)=\operatorname {Card} \{k\,\,\|k<n,\,(k,n)=1\}\quad$	$n$	$\operatorname {H} (s)=\zeta (s-1)$	$\operatorname {G} (s)=\sum _{n=1}^{\infty }{\frac {\varphi (n)}{n^{s}}}={\frac {\zeta (s-1)}{\zeta (s)}}$
除数函数	$n^{\alpha }$	$\sigma _{\alpha }(n)=\sum _{d\|n}d^{\alpha }$	$\operatorname {G} (s)=\zeta (s-\alpha )$	$\operatorname {H} (s)=\sum _{n=1}^{\infty }{\frac {\sigma _{\alpha }(n)}{n^{s}}}=\zeta (s-\alpha )\zeta (s)$
刘维尔函数	$\mu (n)=\mu (p_{1}^{a_{1}}p_{2}^{a_{2}}...p_{k}^{a_{k}})=a_{1}+a_{2}+...+a_{k}$	${\begin{cases}1&n=m^{2}\\0&\mathrm {otherwise} \end{cases}}$	$\operatorname {H} (s)=\zeta (2s)$	$\operatorname {G} (s)=\sum _{n=1}^{\infty }{\frac {\lambda (n)}{n^{s}}}={\frac {\zeta (2s)}{\zeta (s)}}$
冯·曼戈尔特函数	$\Lambda (n)={\begin{cases}\log(p)&n=p^{k}\\0&\mathrm {otherwise} \end{cases}}$	$\log n$	$\operatorname {H} (s)=\zeta '(s)$	$\operatorname {G} (s)=\sum _{n=1}^{\infty }{\frac {\Lambda (n)}{n^{s}}}=-{\frac {\zeta '(s)}{\zeta (s)}}$

佩龙公式

ζ函数与数论函数存在的联系可以通过佩龙公式转化为它和数论函数的求和的关系：设

G(s)={\sum _{n=1}^{\infty }}g(n)

则由佩龙公式，

A(x)={\sum _{n\leq x}}'g(n)={\frac {1}{2\pi i}}\int _{c-i\infty }^{c+i\infty }G(z){\frac {x^{z}}{z}}\,\mathrm {d} z

其中右上角的'表示如果x是整数，那么求和的最后一项要乘以 ${\begin{smallmatrix}{\frac {1}{2}}\end{smallmatrix}}$ 。
这样做的其中一个结果就是ζ函数和素数分布的关系。

和素数的关系

欧拉乘积

此函数和素数的关系已由欧拉所揭示：

\zeta (s)=\prod _{p}{\frac {1}{1-p^{-s}}}

这是一个延展到所有的质数p的无穷乘积，被称为欧拉乘积。这是几何级数的公式和算术基本定理的一个结果。
如果对上式取对数，则可得到

\log \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n}}\sum _{p}p^{-ns}

上式的证明过程

首先留意到

\log ab=\log a+\log b

，由此，可以将乘积转化为求和

{\begin{aligned}\log \zeta (s)&=\log \prod _{p}{\frac {1}{1-p^{-s}}}\\&=\sum _{p}\log {\frac {1}{1-p^{-s}}}\\&=-\sum _{p}\log(1-p^{-s})\\&{\overset {\underset {\mathrm {t=p^{-s}} }{}}{=}}-\sum _{p}\log(1-t)\\\end{aligned}}

将其中的 $\log(1-t)$ 展开为幂级数，得到

{\begin{aligned}-\sum _{p}\log(1-t)&=-\sum _{p}\sum _{n=1}^{\infty }-{\frac {t^{n}}{n}}\\&=\sum _{p}\sum _{n=1}^{\infty }{\frac {t^{n}}{n}}\\&=\sum _{n=1}^{\infty }\sum _{p}{\frac {t^{n}}{n}}\\&=\sum _{n=1}^{\infty }{\frac {1}{n}}\sum _{p}t^{n}\\&{\overset {\underset {\mathrm {p^{-s}=t} }{}}{=}}\sum _{n=1}^{\infty }{\frac {1}{n}}\sum _{p}p^{-ns}\\\end{aligned}}

黎曼阶梯素数计数函数

黎曼素数计数函数（蓝色）J(x)与对数积分（金色）Li(x)的图像，x<300

黎曼素数计数函数（蓝点）J(x)与对数积分（红线）Li(x)的图像，x<1 000 000

可以使用黎曼素数计数函数 ${\begin{smallmatrix}\operatorname {J} (x)\end{smallmatrix}}$ 建立 ${\begin{smallmatrix}\zeta (s)\end{smallmatrix}}$ 与素数分布的进一步联系，这也是黎曼在他的论文论小于给定数值的素数个数中使用的函数，定义如下：

\operatorname {J} (x)=\sum _{n\leq x}\kappa (n)

其中 $\kappa (n)={\begin{cases}{\frac {1}{k}}&n=p^{k}\\0&\mathrm {otherwise} \end{cases}}$
那么可以建立 ${\begin{smallmatrix}\operatorname {J} (x)\end{smallmatrix}}$ 与 ${\begin{smallmatrix}\zeta (s)\end{smallmatrix}}$ 的零点ρ的联系，称为黎曼显式公式

{\begin{aligned}\operatorname {J} (x)&={\frac {1}{2\pi i}}\int _{c-i\infty }^{c+i\infty }\log \zeta (s){\frac {x^{s}}{s}}\,\mathrm {d} s\\&=\operatorname {Li} (x)-\sum _{\rho }\operatorname {Li} (x^{\rho })+\int _{x}^{\infty }{\frac {1}{t(t^{2}-1)\log(t)}}\,\mathrm {d} x-\log 2\\\end{aligned}}

黎曼显式公式的證明

实际上，由J(x)的定义同样有:

\operatorname {J} (x)=\sum _{m=1}^{\infty }{\frac {1}{m}}\pi (x^{\frac {1}{m}})

为使用Mellin 变换，将J(x)乘以 ${\begin{smallmatrix}x^{-s-1}\end{smallmatrix}}$ 后对x积分，得到

{\begin{aligned}\int _{0}^{\infty }\operatorname {J} (x)x^{-s-1}\,\mathrm {d} x&=\sum _{m=1}^{\infty }{\frac {1}{m}}\int _{1}^{\infty }\pi \left(x^{\frac {1}{m}}\right)x^{-s-1}\,\mathrm {d} x\\&=\sum _{m=1}^{\infty }{\frac {1}{m}}\sum _{p}\int _{p^{m}}^{\infty }x^{-s-1}\,\mathrm {d} x\\&=\sum _{m=1}^{\infty }{\frac {1}{m}}\sum _{p}{\frac {1}{s}}p^{-ms}\\\end{aligned}}

注意到 ${\frac {\log \zeta (s)}{s}}={\frac {1}{s}}\sum _{m=1}^{\infty }{\frac {1}{m}}\sum _{p}p^{-ms}$ 与上式相同
即 ${\frac {\log \zeta (s)}{s}}=\int _{0}^{\infty }\operatorname {J} (x)x^{-s-1}\,\mathrm {d} x$
在此处使用Mellin变换后，得到

\operatorname {J} (x)={\frac {1}{2\pi i}}\int _{c-i\infty }^{c+i\infty }{\frac {\log \zeta (s)}{s}}x^{s}\,\mathrm {d} s

(c>1)

再将阿达马乘积公式代入，逐项积分即得所求

而 ${\begin{smallmatrix}\operatorname {J} (x)\end{smallmatrix}}$ 与 ${\begin{smallmatrix}\pi (x)\end{smallmatrix}}$ 的联系可以通过莫比乌斯反演公式完成。
$\pi (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {J} (x)=\operatorname {J} (x)+\mathrm {O} ({\sqrt {x}}\log \log x)$
然而 ${\begin{smallmatrix}\operatorname {J} (x)\end{smallmatrix}}$ 的表达式过于复杂，如下的切比雪夫函数更为常用。

切比雪夫函数

第二切比雪夫函数（蓝线）ψ(x)与y=x（金线）的图像,x<300

第二切比雪夫函数（蓝点）ψ(x)与y=x（红线）的图像,x<1 000 000

第一切比雪夫函数 ${\begin{smallmatrix}\vartheta (x)\end{smallmatrix}}$ 定义为

\vartheta (x)=\sum _{p\leq x}\log p

而更常用的第二切比雪夫函数 ${\begin{smallmatrix}\psi (x)\end{smallmatrix}}$ 定义为

\psi (x)=\sum _{p^{k}\leq x}\log p=\sum _{n\leq x}\Lambda (n)=\sum _{p\leq x}\lfloor \log _{p}x\rfloor \log p

其中，如前文定义的 $\Lambda (n)={\begin{cases}\log(p)&n=p^{k}\\0&\mathrm {otherwise} \end{cases}}$
第二切比雪夫函数与第一切比雪夫函数的关系，可看做“等同于”黎曼素数计数函数与素数计数函数的关系。
第二切比雪夫函数 ${\begin{smallmatrix}\psi (x)\end{smallmatrix}}$ 与 ${\begin{smallmatrix}\zeta (s)\end{smallmatrix}}$ 的零点ρ有如下的联系

{\begin{aligned}\psi (x)&={\frac {1}{2\pi i}}\int _{c-i\infty }^{c+i\infty }-{\frac {\zeta '(s)}{\zeta (s)}}{\frac {x^{s}}{s}}\,\mathrm {d} s\\&=\sum _{n\leq x}\Lambda (n)=x-\sum _{\rho }{\frac {x^{\rho }}{\rho }}-{\frac {1}{2}}\log(1-{\frac {1}{x^{2}}})-\log(2\pi )\\\end{aligned}}

而 ${\begin{smallmatrix}\psi (x)\end{smallmatrix}}$ 与 ${\begin{smallmatrix}\operatorname {J} (x)\end{smallmatrix}}$ 的联系可以通过阿贝尔求和公式：

\psi (x)=\sum _{n=p^{k}\leq x}\log p=\psi (x)=\sum _{n=p^{k}\leq x}{\frac {1}{k}}\log n=\sum _{n\leq x}{\frac {\kappa (n)}{\log n}}

其中κ如前文所定义，则由阿贝尔求和公式

\operatorname {J} (x)=\sum _{n\leq x}\kappa (n)={\frac {\psi (x)}{\log x}}+\int _{2}^{x}{\frac {\psi (t)}{t^{2}\log t}}\,\mathrm {d} t={\frac {\psi (x)}{\log x}}+\mathrm {O} ({\frac {x}{\log ^{2}x}})

零点

解析延拓之后的ζ函数具有零点，他们分别是分布有序的平凡零点（所有负偶数），以及临界带 ${\begin{smallmatrix}0<\operatorname {Re} s<1\end{smallmatrix}}$ 内的非平凡零点。
以 ${\begin{smallmatrix}\operatorname {N} (T)\end{smallmatrix}}$ 表示虚部介于0与T之间的非平凡零点数量，则 ${\begin{smallmatrix}0<\operatorname {N} (T)\end{smallmatrix}}$ 遵循黎曼 - 冯·曼戈尔特公式： $N(T)={\frac {T}{2\pi }}\log {\frac {T}{2\pi }}-{\frac {T}{2\pi }}+\mathrm {O} (\log T)$ 。

函数值

黎曼函数在s > 1的情况

ζ函数满足如下函数方程：

\zeta (s)=2^{s}\pi ^{s-1}\sin \left({\frac {\pi s}{2}}\right)\Gamma (1-s)\zeta (1-s)

对于所有C\{0,1}中的s成立。这裡，Γ表示Γ函数。这个公式原来用来构造解析连续性。在s = 1，ζ函数有一个简单极点其留数为1。上述方程中有sin函數， $\sin \left({\frac {\pi s}{2}}\right)$ 的零點為偶數s = 2n，這些位置是可能的零點，但s為正偶數時， $\sin \left({\frac {\pi s}{2}}\right)\Gamma (1-s)$ 為不為零的規則函數，只有s為負偶數時，ζ函数才有零點，稱為平凡零點。

当s为正整数

欧拉计算出ζ（2k），对于偶整数2k，使用公式

\zeta (2k)={\frac {B_{2k}(-1)^{k+1}(2\pi )^{2k}}{2(2k)!}}

其中B_2k是伯努利数。从这个，我们可以看到ζ(2) = π²/6, ζ(4) = π⁴/90, ζ(6) = π⁶/945等等。（OEIS中的序列A046988（页面存档备份，存于）/A002432（页面存档备份，存于））。这些给出了著名的π的无穷级数。奇整数的情况没有这么简单。拉马努金在这上面做了很多了不起的工作。 $s\,$ 为正偶数时的函数值公式已经由欧拉计算出。但当 $s\,$ 为正奇数时，尚未找到封闭式。

{\displaystyle \zeta (1)=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots =\infty

这是调和级数。

\zeta \left({\frac {3}{2}}\right)\approx 2.612;\!

A078434

该值用于计算具有周期性边界条件的玻色-爱因斯坦凝聚的临界温度以及磁系统的自旋波物理。

\zeta (2)=1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}\approx 1.645;\!

A013661

即巴塞尔问题。这个结果的倒数回答了这个问题：随机选取两个数字而互质的概率是多少？[7]

\zeta (3)=1+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+\cdots \approx 1.202;\!

A002117

称为阿培里常數。

\zeta (4)=1+{\frac {1}{2^{4}}}+{\frac {1}{3^{4}}}+\cdots ={\frac {\pi ^{4}}{90}}\approx 1.0823;\!

A0013662

黑體輻射裡的斯特藩－玻尔兹曼定律和维恩近似。

s趨近於1

\lim _{\varepsilon \to 0}{\frac {\zeta (1+\varepsilon )+\zeta (1-\varepsilon )}{2}}=\gamma

其中γ是歐拉-馬歇羅尼常數= $0.577215...$

负整数

同样由欧拉发现，ζ函数在负整数点的值是有理数，这在模形式中发挥着重要作用，而且ζ函数在负偶整数点的值為零。

事實上

\zeta (-n)=-{\frac {B_{n+1}}{n+1}}

B_n是白努利數。

因為 B_2n+1 =0，故ζ函数在负偶整数点的值為零。

复数值

\zeta (x+{\rm {i}}y)=\sum _{k=1}^{\infty }{\frac {\cos(y\ln k)-{\rm {i}}\sin(y\ln k)}{k^{x}}},y\in {\mathbb {R} }

，x＞1。

幅角

\arg[\zeta (x+{\rm {i}}y)]=-\arctan {\frac {\sum _{k=1}^{\infty }{\frac {\sin(y\ln k)}{k^{x}}}}{\sum _{k=1}^{\infty }{\frac {\cos(y\ln k)}{k^{x}}}}}

，

函数值表

\zeta (-2n_{n\in \mathbb {Z} ^{+}})=0

，

\zeta (-9)=-{\frac {1}{132}}({\mathfrak {R}})

，

\zeta (-7)={\frac {1}{240}}({\mathfrak {R}})

，

\zeta (-5)=-{\frac {1}{252}}({\mathfrak {R}})

，

\zeta (-3)={\frac {1}{120}}({\mathfrak {R}})

，

\zeta (-1)=-{\frac {1}{12}}({\mathfrak {R}})

，

\zeta (0)=-{\frac {1}{2}}

，

\zeta (1^{-})=-\infty

,

\zeta (1^{+})=\infty

,

\zeta (2)={\frac {\pi ^{2}}{6}}

，

\zeta (4)={\frac {\pi ^{4}}{90}}

，

\zeta (6)={\frac {\pi ^{6}}{945}}

，

\zeta (8)={\frac {\pi ^{8}}{9450}}

，

\zeta (10)={\frac {\pi ^{10}}{93555}}

，

临界线上的数值计算

临界线上的数值计算可以通过黎曼-西格尔公式完成。
与之相关的，林德勒夫猜想：对于任意给定的實数 ${\begin{smallmatrix}\epsilon >0\end{smallmatrix}}$ ，

\zeta \left({\frac {1}{2}}+it\right)=\mathrm {O} (t^{\epsilon })

參考資料

. [2015-01-17]. （原始内容存档于2015-03-20）.
Devlin, Keith. . New York: Barnes & Noble. 2002: 43–47. ISBN 978-0760786598.
Tom M.Apostol. . 北京: 世界图书出版公司北京公司. 2012年1月: 55 – 56. ISBN 978-7-5100-4062-7 （英语）. Theorem 3.2 If x ≥ 1 we have :
御坂01034. . [2015-01-24]. （原始内容存档于2019-05-02）.
加藤和也黑川信重斎藤毅. . 北京: 高等教育出版社. 2009年6月: 197–199. ISBN 978-7-04-026360-2 （中文）. 短暂的沉默被打破了...
加藤和也黑川信重斎藤毅. . 北京: 高等教育出版社. 2009年6月: 209–210. ISBN 978-7-04-026360-2 （中文）. Riamann对ζ研究的全部内容...
C. S. Ogilvy & J. T. Anderson Excursions in Number Theory, pp. 29–35, Dover Publications Inc., 1988 ISBN 978-0-486-25778-5