三複合正八面體
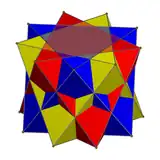
在幾何學中,三複合正八面體是一個由3個正八面體所組成的幾何結構,在這個結構中,每個正八面體都將對於其他正八面體有一個相同旋轉中心的旋轉關係。其最早於布鲁克纳在數學文獻中提及,後來莫里茲·柯尼利斯·艾雪用此形狀於1948年創作了木刻作品《群星》。
 | ||
| 類別 | 複合多面體 | |
|---|---|---|
| 對偶多面體 | 三複合立方體 | |
| 性質 | ||
| 體 | 3 | |
| 面 | 24 | |
| 邊 | 36 | |
| 頂點 | 18 | |
| 歐拉特徵數 | F=24, E=36, V=18 (χ=6) | |
| 組成與佈局 | ||
| 複合幾何體數量 | 3 | |
| 複合幾何體種類 | 3個正八面體 | |
| 面的種類 | 正三角形 | |
| 對稱性 | ||
| 對稱群 | Oh, 48階 | |
| 旋轉對稱群 | O, [4,3]+, (432) | |
| 特性 | ||
| 面可遞 | ||
| 圖像 | ||
| ||
性質
三複合正八面體是一種複合多面體,由3個正八面體組成,共具有24個面、36條邊和18個頂點,正好是正八面體的三倍。[1]
結構
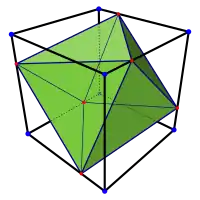
正八面體可以透過將其頂點置於立方體的一對正方形面的八條稜上內接在立方體內[2]。
對於一個立方體共有三個相對面可以完成上述內嵌的動作,透過這個方式依序將三個正八面體內接在立方體內則可以構成三複合正八面體[2]。三複合正八面體中三個正八面體互相相交的稜,其相交時產生的八個頂點正好也可以構成一個立方體[3]。每組而互相相交的三條稜其交點正好將之分割成長度比為1:√2的兩線段[3]。其餘的八面體邊成對地在立體的內部彼此相交,其交點正好將邊均分為二,這意味著其交點正好位於邊的中點;另外,其交角恰好為直角。
作法
三複合正八面體可透過取三個全等的八面體,先使其重合,並以其中一個正八面體為準,並圍繞著過基準正八面體之兩相對頂點的對稱軸旋轉π/4(45度角),符合上述條件的對稱軸共有三個,三個正八面體每個分別對著三軸的其中一軸旋轉,即可構成三複合正八面體[4]。此外,三複合正八面體也可以對三複合立方體取對偶多面體來構造。
對稱性

三複合正八面體的對稱性與單一一個正八面體相同,皆為八面體群對稱性[6]。其可以視為一個等邊三角面多面體,這意味著其面為正三角形,具有面可遞的性質,這意味著,這立體上的任意兩個面A和B,透過旋轉或鏡射這個立體,使A移動到B原來的位置時,其面仍然佔據了相同的空間區域[7]。目前已知的等邊三角面多面體有一個已知的無窮序列,但已知有36種等邊三角面多面體不屬於這個序列,而三複合正八面體正是這36個例外之一[8]。雖三複合正八面體有面可遞的性質,但由於其不具有點可遞的性質因此不屬於均勻多面體複合體。
在三複合正八面體中,由三個正八面體共同相交出來的區域是一個四角化六面體,其具有24個面,並可以視為在立方體的每個面上疊上四角錐的結果[3]。而四角化六面體的面皆可以與三複合正八面體的其中一個面共面,因此三複合正八面體也可以視為是一種星形四角化六面體,即四角化六面體的星形化體。另外有一種形式的四角化六面體也為等邊三角面多面體,其同樣是在立方體的每個面上疊上四角錐的結果,但加入的四角錐之錐高比卡塔蘭立體的四角化六面體更高,使得四角錐的側面變成正三角形(等邊三角形),並形成凹多面體,其正三角形面也與三複合正八面體的面位於相同的平面上;這是另外一個已知也與三複合正八面體的面位於相同的平面上的等邊三角面多面體。第三種已知也與三複合正八面體的面位於相同的平面上的幾何結構是六複合正四面體,其為三複合正八面體的三個正八面體星形化成星形八面體的結果。第四種已知也與三複合正八面體的面位於相同的平面上的幾何結構同樣是三複合正八面體的星形化體,其排列方式與四角化六面體相同,但其加入的是倒錐體,即將立方體的面替換成向內凹陷的四角錐側面。[8]
歷史
在皮耶羅·德拉·弗朗西斯卡的15世紀手稿《Libellus De Quinque Corporibus Regularibus》中,德拉·弗朗西斯卡描繪了圍繞著立方體內接的正八面體圖形,其立方體的其中八條邊分別位於正八面體的八個面上。若將三個正八面體以上述方式內接入立方體中則可以形成三複合正八面體,不過德拉·弗朗西斯卡並未描繪這種幾何結構[9]。
第二次在數學文獻中出現三複合正八面體是馬克斯·布呂克納於1900年的研究中,其在文獻中提及了三複合正八面體並包括它的模型的照片。[3][10]
荷蘭藝術家莫里茲·柯尼利斯·艾雪,在他1948年的木刻作品《群星》中使用三複合正八面體作為木刻的主要元素,其描繪了一個漂浮在太空中的三複合正八面體形狀的籠子,且這個形狀的籠子裡有兩隻變色龍[11]。然而艾雪從未閱讀過馬克斯·布呂克納的研究,因此被哈罗德·斯科特·麦克唐纳·考克斯特注意到,並說道:「值得注意的是,艾雪在沒有任何代數或解析幾何知識的情況下,能夠重新發現這種高度對稱的幾何結構。[註 1]」,因此可以視為艾雪在布呂克納的研究發表後又獨立發現了三複合正八面體[3]。在1948年早些時候,艾雪做了一個類似主題的木刻初稿《研究星體》,不過在這個初稿中沒有使用三複合正八面體,而是使用了星形四角化菱形十二面體,其雖然不是三複合正八面體,但這一種形狀一定程度上與三複合正八面體相關——它可以視為三個較扁的正八面體之複合體,而這個立體有時會被稱為艾雪立體。[12]這個立體拓樸結構與四角化菱形十二面體相同,皆可以視為將菱形十二面體的每個菱形面替換成菱形錐(底面為菱形的四角錐)的結果。三複合正八面體的對偶多面體是三複合立方體,其也出現於艾雪的木刻作品中,位於木刻作品《瀑布》中,星形四角化菱形十二面體旁邊的立體。[11]
其他的三複合正八面體
三個正八面體除了可以透過上述方式組合外,亦有其他組合方式,但通常會討論具有較高對稱性的形式。另一種對稱性較高的三複合正八面體是將正八面體視為三角反稜柱,三個三角反稜柱可以形成具有D3d、階數為12之對稱性的均勻角柱狀複合反角柱,每個三角反稜柱皆相對於其他三角反稜柱旋轉了40度,其頂面可以視為是一個複合圖形組成的九角星,在施萊夫利符號中可以用{9/3}或3{3}表示。[13]
註解
- 原文為:「It is remarkable that Escher, without any knowledge of algebra or analytic geometry, was able to rediscover this highly symmetrical figure.」
參見
- 四複合正八面體
- 五複合正八面體
- 十複合正八面體
- 二十複合正八面體
參考文獻
- Thull. . origametry.net. [2019-09-18]. (原始内容存档于2021-05-08).
- Bakos, T.; Johnson, Norman W., , The Mathematical Gazette, 1959, 43 (343): 17–20, JSTOR 3608867
- Coxeter, H. S. M., , The Mathematical Intelligencer, 1985, 7 (1): 59–69, doi:10.1007/BF03023010. The discussion of the compound of three octahedra is on pp. 61–62.
- Wenninger, M. J., , The Mathematical Gazette, 1968, 52 (379): 16–23, JSTOR 3614454
- Weisstein, Eric W. . MathWorld--A Wolfram Web Resource. [2019-09-07]. (原始内容存档于2019-09-02).
- Cromwell, P.R. . Cambridge University Press. 1999: 363. ISBN 9780521664059. LCCN 96009420.
- McLean, K. Robin, , The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822.
- Shephard, G. C., , Periodica Mathematica Hungarica, 1999, 39 (1–3): 83–106, doi:10.1023/A:1004838806529.
- Hart, George W., , , 1998 [2019-09-09], (原始内容存档于2017-11-26).
- Brückner, Max, , Leipzig: Teubner, p. 188 and Tafel VIII 12, 1900. As cited by Coxeter (1985).
- Hart, George W., , , 1996 [2019-09-09], (原始内容存档于2019-01-15).
- The compound of three octahedra and a remarkable compound of three square dipyramids, the Escher's solid (页面存档备份,存于), Livio Zefiro, University of Genova.
- Skilling, John, , Mathematical Proceedings of the Cambridge Philosophical Society, 1976, 79 (3): 447–457, MR 0397554, doi:10.1017/S0305004100052440