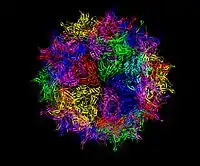
五角化十二面體
在幾何學中,五角化十二面體(Pentakis dodecahedron)是一種六十面體[1],指經過五角化變換的正十二面體[2],換句話說,五角化十二面體是將正十二面體的每個正五邊形面替換為五角錐後所形成的立體。當五角錐的錐高恰好使得所形成之立體的所有二面角等角時,則該幾何形狀是一種卡塔蘭立體[3],為截角二十面體的對偶多面體。一般五角化二十面體一詞用來稱呼卡塔蘭立體的版本,即凸多面體的版本,而更高的錐高會使得其成為非凸多面體,例如小星形十二面體[4]。
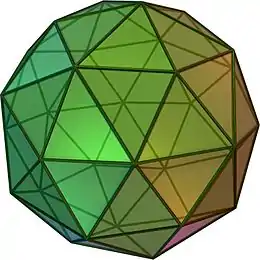 (按這裡觀看旋轉模型) | ||||
| 類別 | 卡塔蘭立體 | |||
|---|---|---|---|---|
| 對偶多面體 | 截角二十面體 | |||
| 識別 | ||||
| 鮑爾斯縮寫 | pakid | |||
| 數學表示法 | ||||
| 考克斯特符號 | ||||
| 康威表示法 | kD | |||
| 性質 | ||||
| 面 | 60 | |||
| 邊 | 90 | |||
| 頂點 | 32 | |||
| 歐拉特徵數 | F=60, E=90, V=32 (χ=2) | |||
| 二面角 | 153°43′6.79342″ arccos(−80 + 9√5/109) | |||
| 組成與佈局 | ||||
| 面的種類 | 等腰三角形 | |||
| 頂點的種類 | 20個6階頂點 12個階5頂點 20{6}+12{5} | |||
| 對稱性 | ||||
| 對稱群 | Ih, H3, [5,3], (*532) | |||
| 旋轉對稱群 | I, [5,3]+, (532) | |||
| 圖像 | ||||
| ||||
性質
五角化十二面體由60個面、90條邊和32個頂點組成[5],其中60個面皆為全等的等腰三角形組成;在其32個頂點中,其中20個頂點是6個面的公共頂點、12個頂點是5個面的公共頂點[6][7]。由於其具有32個頂點,因此對偶多面體是一個三十二面體,為截角二十面體[8]。五角化十二面體可透過在正十二面體的每個面上疊上錐體構成[9],當其錐高恰好使得所形成之立體的所有二面角等角時,則該幾何形狀是一種卡塔蘭立體[3],在這個情況下,其對應的對偶多面體為一個半正三十二面體。
若將五角化十二面體,五角化變換的原像——正十二面體視為三維類五邊形形[10],則五角化十二面體可以視為五邊形五邊各加一個等腰三角形拼成的正十邊形在立體幾何中的推廣。
構造
五角化十二面體可由正十二面體經過五角化變換來構造。五角化十二面體是將正十二面體的每個正五邊形面替換為五角錐後所形成的立體[2]。根據錐高的不同,會使地所構成的立體有不同性質。要確保所構成的立體為嚴格凸多面體(即沒有面兩兩共面的情況)其加入角錐的錐高不能超過[3]:
其中,為原像多面體的邊長。
若錐高等於時,所形成的立體將會出現三角形兩兩共面的情況,若將每個兩兩共面的三角形是為菱形[9]:167,則所構成的立體為菱形三十面體。[3]更高的錐高將導致所形成的立體變為非凸多面體[9]:167,例如小星形十二面體為加入的錐高為時的情況[4]。
要成為塔卡蘭立體,五角化十二面體在五角化的過程必須確保所加入的角錐後的結果所有二面角相等,要達成這個目標所要加入的角錐錐高須為:[3]
應用
在化學中
部分分子的形狀是五角化十二面體,例如Au20Si12[12]。
巴克明斯特富勒烯(C60)分子模型中會形成類似五角化十二面體的外型,其中五角化十二面體的每個面對應著一個碳原子,類似的現象也會出現在石狮子雕塑中的球狀物中[13]。等效地,截角二十面體是富勒烯分子模型對應的多面體,每個頂點代表一個碳原子。[14]
文化引用
華特迪士尼世界度假區未來世界的太空船地球號結構是五角化十二面體的細分結果[17]。
變體
當每面疊上的五角錐的高不能使是整個立體的二面角皆相等時,就會有如下情況:
| 圖像 | 名稱 | 加入錐體的方式 | 錐高 |
|---|---|---|---|
 |
複合大三角六邊形二十面體凹五角錐十二面體 | 加入倒五角錐並從另外一側穿出 | |
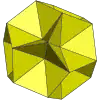 |
凹五角錐十二面體 | 加入倒五角錐 | |
 |
正十二面體 | 原始形狀 | 0 |
 |
五角化十二面體 | 加入到能使所有二面角等角的高度 | 0.251[3]
|
 |
菱形三十面體 | 加入到面兩兩共面的高度 | 0.425[3]
|
 |
小星形十二面體 | 1.37638 | |
 |
大五角化十二面體 |
參見
參考文獻
- Pascual-Ahuir, JL and Silla, E and Tomasi, J and Bonaccorsi, R. . Journal of Computational Chemistry (Wiley Online Library). 1987, 8 (6): 778–787.
- Çolak, Zeynep and Gelişgen, Özcan. . Sakarya Üniversitesi Fen Bilimleri Enstitüsü Dergisi. 2015, 19 (3): 353–360.
- Livio Zefiro; Maria Rosa Ardig. . mi.sanu.ac.rs. [2021-07-22]. (原始内容存档于2021-05-06).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Rene K. Mueller. . simplydifferently.org. 2007 [2021-08-10]. (原始内容存档于2021-08-11).
- Konstantinidis, NP. . arXiv preprint arXiv:2101.06739. 2021.
- Robert Whittaker. . polyhedra.mathmos.net. [2021-08-10]. (原始内容存档于2021-08-10).
- De Witte, Erik and Marantis, Leonidas and Tong, Kin-Fai and Brennan, Paul and Griffiths, Hugh. . 2006 First European Conference on Antennas and Propagation (IEEE). 2006: 1–5.
- Pearce, P. . MIT Press. 1980: 160 [2021-08-10]. ISBN 9780262660457. LCCN 77026866. (原始内容存档于2021-08-10).
- Coxeter, Harold Scott MacDonald, , New York: Dover Publications, 1973, ISBN 978-0-486-61480-9
- . Fillygons. [2021-08-10]. (原始内容存档于2021-08-10).
- Guo, JJ and Zhao, HY and Wang, J and Ai, LY and Liu, Y. . The Journal of chemical physics (AIP Publishing LLC). 2017, 146 (6): 064310.
- Katz, Eugene A and Jin, Bih-Yaw. . The Mathematical Intelligencer (Springer). 2016, 38 (3): 61–68.
- Katz, E. A. . Sōga, Tetsuo (编). . Elsevier. 2006: 374 [2021-08-13]. ISBN 978-0-444-52844-5. (原始内容存档于2021-03-18).
- Sonntag F, Schmidt K, Kleinschmidt JA. . Proceedings of the National Academy of Sciences of the United States of America. June 2010, 107 (22): 10220–5. Bibcode:2010PNAS..10710220S. PMC 2890453
 . PMID 20479244. doi:10.1073/pnas.1001673107.
. PMID 20479244. doi:10.1073/pnas.1001673107. - Raguram, Aditya and Sasisekharan, V and Sasisekharan, Ram. . Trends in microbiology (Elsevier). 2017, 25 (6): 438–446.
- Rene K. Mueller. . simplydifferently.org. 2007 [2021-08-10]. (原始内容存档于2021-08-11).