代數曲線

曲線在一點${\displaystyle P}$的平滑性可以用雅可比矩陣判斷。以下考慮嵌於${\displaystyle \mathbb {P} ^{n}}$中的曲線：設該曲線由${\displaystyle n-1}$個${\displaystyle n+1}$個變元的齊次多項式${\displaystyle g_{1},\ldots ,g_{n-1}}$定義，若其雅可比矩陣${\displaystyle \left({\frac {\partial g_{i}}{\partial x_{j}}}\right)_{i,j}}$在區線上一點${\displaystyle P}$滿秩，則稱它${\displaystyle P}$點光滑；反之則稱為奇點。在一點的平滑性與多項式${\displaystyle g_{1},\ldots ,g_{n-1}}$的選取無關，也與曲線的嵌入方式無關。

在平面射影曲線的例子，假設曲線${\displaystyle C}$由齊次方程式${\displaystyle f(x,y,z)=0}$定義，則${\displaystyle C}$的奇點恰為${\displaystyle C}$上使得${\displaystyle \nabla f}$為零的點，即：

${\displaystyle {\frac {\partial f}{\partial x}}(P)={\frac {\partial f}{\partial y}}(P)={\frac {\partial f}{\partial z}}(P)=0\quad (P\in C)}$

在特徵非零的域上，一條代數曲線僅有有限個奇點；無奇點的曲線即平滑曲線。奇點在雙有理映射下可能映為光滑點；事實上，奇點總是可藉著平面的拉開映射或正規化解消，由此得到的新平滑曲線仍雙有理等價於原曲線；然而對代數封閉域上的射影曲線，其奇點總數則關係到曲線的幾何虧格，後者是個雙有理不變量。

x³ = y²

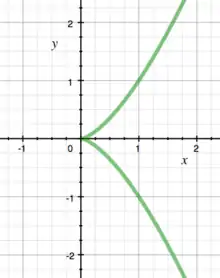
曲線的奇點包括多重點（這是曲線的自交點）及尖點（如仿射曲線${\displaystyle x^{3}=y^{2}}$之於原點${\displaystyle (0,0)}$，見右圖）等等。一般來說，仿射平面曲線${\displaystyle f(x,y)=0}$在一點${\displaystyle P}$的奇點性質可以透過下述方式理解：

透過平移，不妨假設${\displaystyle P=(0,0)}$。將多項式${\displaystyle f(x,y)}$寫成

${\displaystyle f(x,y)=\sum _{n\geq 1}f_{n}(x,y)}$

其中${\displaystyle f_{n}(x,y)}$是${\displaystyle n}$次齊次多項式。直觀地想像，${\displaystyle f(x,y)=0}$在原點附近的性狀僅決定於最低次的非零項，設之為${\displaystyle f_{m}(x,y)}$。根據齊次性可以將之分解成

${\displaystyle f_{m}(x,y)=\prod _{i=1}^{m}(a_{i}x-b_{i}y)}$

換言之，曲線在原點附近將近似於${\displaystyle m}$條（含重複）直線${\displaystyle a_{i}x-b_{i}y=0}$的聯集。上式中相異的直線數${\displaystyle r}$稱作分支數，正整數${\displaystyle m}$稱作平面曲線在該點的重數，此外還有一個內在的不變量${\displaystyle \delta _{P}:=\dim {\mathcal {O}}_{{\tilde {C}},P}/{\mathcal {O}}_{C,P}}$，其中${\displaystyle {\tilde {C}}\rightarrow C}$是該曲線的正規化態射。資料[m, δ, r]能夠被用來分類奇點。例如一般尖點對應到${\displaystyle [2,1,1]}$，一般雙重點對應到${\displaystyle [2,1,2]}$，而一般n重點則對應到${\displaystyle [n,{\frac {n(n-1)}{2}},n]}$。

各奇點的不變量δ_P決定平面曲線${\displaystyle f(x,y)=0}$的虧格：設${\displaystyle \deg f=d}$，則有

${\displaystyle g={\frac {1}{2}}(d-1)(d-2)-\sum _{P}\delta _{P},}$

對於在複數域上的平面曲線，John Milnor以拓撲方式定義了不變量μ，稱為Milnor數：同樣假設${\displaystyle P=(0,0)}$，在原點附近夠小的四維球${\displaystyle B_{\epsilon }:=\{(x,y)\in \mathbb {C} ^{2}:|x|^{2}+|y|^{2}<\epsilon \}}$內有${\displaystyle (x,y)\neq (0,0)\Rightarrow \nabla f(x,y)\neq 0}$，此時有連續映射

${\displaystyle \nabla f(x,y):B_{\epsilon }-\{(0,0)\}\rightarrow B_{\epsilon }-\{(0,0)\}}$

由於${\displaystyle B_{\epsilon }-\{(0,0)\}}$ 同倫等價於三維球面${\displaystyle \mathbb {S} ^{3}}$，於是可定義μ為此映射的拓撲次數。μ與前述不變量的關係由下式表明：

${\displaystyle \mu =2\delta -r+1}$

事實上，${\displaystyle \{(x,y)\in \mathbb {C} ^{2}:f(x,y)=0\}\cap \{(x,y)\in \mathbb {C} ^{2}:|x|^{2}+|y|^{2}=\epsilon \}}$在ε夠小時是${\displaystyle \{(x,y)\in \mathbb {C} ^{2}:|x|^{2}+|y|^{2}=\epsilon \}\cong \mathbb {S} ^{3}}$中的一個環圈，稱作奇點環圈，它具有複雜的拓撲性質。例如：${\displaystyle x^{3}=y^{2}}$在尖點附近的奇點環圈是三葉結。

域${\displaystyle F}$上的有理曲線是雙有理等價於射影直線${\displaystyle \mathbb {P} _{F}^{1}}$的曲線，換言之，其函數域同構於單變元有理函數域${\displaystyle F(t)}$。當${\displaystyle F}$代數封閉時，這也等價於該曲線之虧格為零，對一般的域則不然；實數域上由${\displaystyle x^{2}+y^{2}+1=0}$給出的函數域虧格為零，而非有理函數域。

具體地說，一條有理曲線是能以有理函數參數化的曲線，例子請見條目有理正規曲線。

任何${\displaystyle F}$上有有理點的圓錐曲線都是有理曲線。參數化的過程如下：過給定有理點${\displaystyle P}$而斜率為${\displaystyle t}$的直線交平面上一條二次曲線於兩點，就x坐標來說，交點的x坐標是一個二次多項式的根，其中一個屬於${\displaystyle F}$的根已知，即${\displaystyle P}$的x坐標；因此透過根與係數的關係得知另一根也屬於${\displaystyle F}$，而且能表作${\displaystyle t}$在${\displaystyle F}$上的有理函數。y坐標的作法相同。

x² + xy + y² = 1

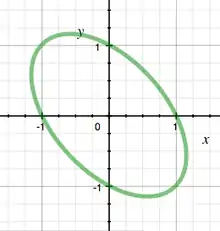
例。考慮斜橢圓${\displaystyle E:x^{2}+xy+y^{2}=1}$，其中${\displaystyle (-1,0)}$是有理點。畫一條過該點且斜率為t之直線${\displaystyle y=t(x+1)}$，並帶入E的等式，於是得到：

${\displaystyle x={\frac {1-t^{2}}{1+t+t^{2}}}}$。

${\displaystyle y=t(x+1)={\frac {t(t+2)}{1+t+t^{2}}}}$

這就給出E的有理參數化，於是證明了E是有理曲線。

將此結果置於射影幾何的框架下，則能導出若干數論的結論。例如我們可在E中加入無窮遠點，得到射影曲線

${\displaystyle X^{2}+XY+Y^{2}=Z^{2}\,\!}$

以上參數化遂表為

${\displaystyle X=1-t^{2},\quad Y=t(t+2),\quad Z=t^{2}+t+1\,\!}$

若取${\displaystyle t}$為整數，對應的${\displaystyle X,Y,Z}$是不定方程${\displaystyle X^{2}+XY+Y^{2}=Z^{2}}$的整數解；若將${\displaystyle X}$代以${\displaystyle -X}$，則此方程詮釋為θ=60°時的餘弦定理，藉此能描述所有一角為 60°且邊長均為整數的三角形，例如取${\displaystyle t=2}$，就得到邊長分別為X=3, Y=8, Z=7的三角形。

橢圓曲線可以定義為任意虧格等於一且給定一個有理點的代數曲線，它們都同構於平面上的三次曲線。此時通常取無窮遠處的反曲點為給定的有理點，這時該曲線可以寫作射影版本的Tate-魏爾施特拉斯形式：

${\displaystyle y^{2}z+a_{1}xyz+a_{3}yz^{2}=x^{3}+a_{2}x^{2}z+a_{4}xz^{2}+a_{6}z^{3}.\,\!}$

橢圓曲線帶有唯一的阿貝爾群結構，使得給定有理點為單位元素，且加法為代數簇的態射，因而橢圓曲線構成一個阿貝爾簇。在三次平面曲線的情形，三點和為零若且唯若它們共線。對於複數域上的橢圓曲線，此阿貝爾簇同構於${\displaystyle \mathbb {C} /\Lambda }$，其中的${\displaystyle \Lambda }$由相應的橢圓函數給出。

對虧格大於一的曲線，其性質與有理曲線與橢圓曲線有顯著不同。根據法爾廷斯定理，定義在數域上的這類曲線只有有限個有理點；若視為黎曼曲面，它們則帶有雙曲幾何的結構。例子包括超橢圓曲線、克萊因四次曲線與一開始提到的費馬曲線在${\displaystyle n\geq 4}$的情形。