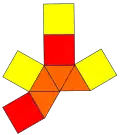
四角錐柱
在幾何學中,四角錐柱是底面為四邊形的角錐柱,其可以視為將底面全等的四角錐與四角柱疊合所形成的立體,又稱為方尖碑(Obelisk)[1]。若底面為正方形則稱為正四角錐柱,等邊的正四角錐柱是一種詹森多面體[1]。四角錐柱具有9個面、16個邊、和9個頂點,每個四角錐柱皆為一個九面體。
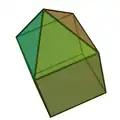 | ||||
| 類別 | 棱錐柱 詹森多面體 J7 - J8 - J9 | |||
|---|---|---|---|---|
| 對偶多面體 | 四角錐柱(自身對偶) | |||
| 識別 | ||||
| 鮑爾斯縮寫 | esquipy | |||
| 數學表示法 | ||||
| 康威表示法 | P4+Y4 | |||
| 性質 | ||||
| 面 | 9 | |||
| 邊 | 16 | |||
| 頂點 | 9 | |||
| 歐拉特徵數 | F=9, E=16, V=9 (χ=2) | |||
| 組成與佈局 | ||||
| 面的種類 | 4個三角形 5個正方形 | |||
| 頂點佈局 | 4個(43) 1個(34) 4個(32.42) | |||
| 對稱性 | ||||
| 對稱群 | C4v, [4], (*44) | |||
| 旋轉對稱群 | C4, [4]+, (44) | |||
| 特性 | ||||
| 凸、demi-regular | ||||
| 圖像 | ||||
| ||||
詹森多面體
考慮一個正四角錐柱,若每一個面皆為正多邊形,則為92種Johnson多面體(J8)中的其中一個,也是角錐柱的一種,可由詹森多面體中的正四角錐與柏拉圖立體中的立方體於相等大小的正方形面接合而組成,這種立體又稱為側錐立方體(augmented cube)[2]。詹森多面體是凸多面體,面皆由正多邊形組成但不屬於均勻多面體,共有92種。這些立體最早在1966年由諾曼·詹森(Norman Johnson)命名並給予描述[3]。
性質
正四角錐柱共由9個面、16條邊、和9個頂點組成[4][5][2][6]。在其9個面中,有4個正三角形面和5個正方形面[4]。在其9個頂點中,有3種頂點,分別是4個三角形的公共頂點,在頂點圖中可以用[34]來表示[7],這種頂點有1個[2]、另一種頂點為2個三角形和2個正方形的公共頂點,在頂點圖中可以用[32,42]來表示[7],這種頂點有4個[2]、還有一種頂點是3個正方形的公共頂點,在頂點圖中可以用[43]來表示[7],這種頂點有4個[2]。
二面角
正四角錐柱共有3種二面角,分別為三角形和正方形的二面角、三角形和三方形的二面角以及正方形和正方形的二面角[7]。其中正方形和正方形的二面角為直角,即90度角。[7]
- 正方形正方形
而三角形和正方形的二面角為負根號三分之二的反餘弦值,約為144.7356度:[7]
- 三角形正方形
三角形和三方形的二面角為負三分之一的反餘弦值,約為109.471度:[7]
- 三角形三方形
對偶多面體
四角錐柱的對偶多面體為四角錐台錐,由4個三角形、1個正方形和4個梯形組成。
| 四角錐柱的對偶多面體 | 對偶多面體的展開圖 |
|---|---|
 |
 |
相關多面體
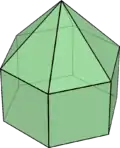
四角錐柱是以四邊形為底的角錐柱。[1]以其他多邊形為底的角錐柱有:
| 二角錐柱 | 三角錐柱 | 四角錐柱 | 五角錐柱 | 六角錐柱 | 七角錐柱 | ... | 圓錐柱 |
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
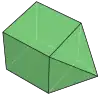
四角錐柱可以視為側錐四角柱,其為底面為四邊形之柱體對應的側錐柱體,其他的側錐柱體有:
| 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|
 |
 |
 |
 |
 |
| 側錐三角柱 | 側錐四角柱 | 側錐五角柱 | 側錐六角柱 | 側錐七角柱 |
此外,正四角錐柱可以與正四面體共同填滿空間[10]。
參考文獻
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- . polyhedra.tessera.li. [2022-09-07]. (原始内容存档于2022-09-07).
- Johnson, Norman W., , Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
- David I. McCooey. . [2022-09-07]. (原始内容存档于2022-09-07).
- . qfbox.info. [2022-09-07]. (原始内容存档于2022-10-05).
- V. Bulatov. . [2022-09-07]. (原始内容存档于2022-05-22).
- Richard Klitzing. . bendwavy.org. [2022-09-07]. (原始内容存档于2022-11-14).
- Sapiña, R. . Problemas y Ecuaciones. [2020-08-28]. ISSN 2659-9899. (原始内容存档于2020-09-30) (西班牙语).
- David I. McCooey. . [2022-09-07]. (原始内容存档于2022-09-07).
- . woodenpolyhedra.web.fc2.com. [2022-09-07]. (原始内容存档于2022-08-07).