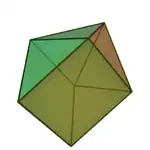
側錐三角柱
側錐三角柱(英文:Augmented triangular prism)屬於詹森多面體之一,索引為J49[1],可由一個正四角錐(J1)和正三角柱分別以底面和側面相互黏合而成[1]。它在外觀上與異相雙三角柱(J26)十分相像,唯一的差別在於前者以正四角錐取代了後者的一個三角柱。它與二側錐三角柱(J50)和三側錐三角柱(J51)有著類似的構造。詹森多面體是凸多面體,面皆由正多邊形組成但不屬於均勻多面體,共有92種。這些立體最早在1966年由諾曼·詹森(Norman Johnson)命名並給予描述[2]。
 | ||
| 類別 | 詹森多面體 J48 - J49 - J50 | |
|---|---|---|
| 識別 | ||
| 名稱 | 側錐三角柱 | |
| 參考索引 | J49 | |
| 鮑爾斯縮寫 | autip | |
| 性質 | ||
| 面 | 8 | |
| 邊 | 13 | |
| 頂點 | 7 | |
| 歐拉特徵數 | F=8, E=13, V=7 (χ=2) | |
| 組成與佈局 | ||
| 面的種類 | 6個三角形 2個正方形 | |
| 頂點圖 | 2個(3.42) 1個(34) 4個(33.4) | |
| 對稱性 | ||
| 對稱群 | C2v群 | |
| 特性 | ||
| 凸 | ||
| 圖像 | ||
| ||
性質
側錐三角柱共由8個面、13條邊和7個頂點組成[3][4][5]。在其8個面中,有6個正三角形面和2個正方形面。側錐三角柱可以視為三角柱與2個正四角錐的組合[6]:86,因此側錐三角柱的6個三角形面又可以分成兩組,一組為側錐的側面,有4個正三角形,以及三角柱的兩個三角形底面。在其7個頂點中,有1個頂點是4個三角形的公共頂點[5],在頂點圖中可以用[34]來表示[7]、還有4個頂點是3個三角形和1個正方形的公共頂點[5],在頂點圖中可以用[33,4]來表示[7]、剩下的2個頂點是1個三角形和2個正方形的公共頂點[5],在頂點圖中可以用[3,42]來表示[7]。
二面角
側錐三角柱有5種二面角,分別是2種三角形與三角形的二面角、2種三角形與正方形的二面角以及1種正方形與正方形的二面角。[7]其中正方形與正方形的二面角為60度。[7]
- 正方形正方形
2種三角形與三角形的二面角分別為側錐與三角柱交會處的三角形與三角形的二面角以及側錐上的三角形與三角形的二面角。
- 其中,側錐與三角柱交會處的三角形與三角形的二面角角度為負三分之二平方根的反餘弦值,角度約為144.7度:[7]
- 而,側錐與三角柱交會處的三角形與三角形的二面角角度為負三分之一的反餘弦值,約為109.471度:[7]
2種三角形與正方形的二面角分別為側錐與三角柱交會處的三角形與正方形的二面角以及三角柱上的三角形與正方形的二面角。
相關多面體
側錐三角柱是1個側面被四角錐取代的三角柱。其他也是側面被取代的三角柱結構有二側錐三角柱和三側錐三角柱。[6]:86
 側錐三角柱
側錐三角柱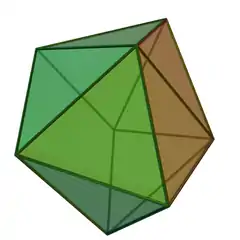
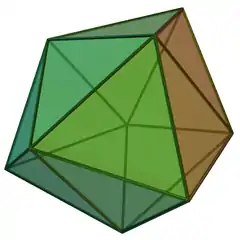
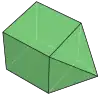
側錐三角柱是底面為三角形之柱體對應的側錐柱體,其他的側錐柱體有:
| 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|
 |
 |
 |
 |
 |
| 側錐三角柱 | 側錐四角柱 | 側錐五角柱 | 側錐六角柱 | 側錐七角柱 |
參考文獻
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Johnson, Norman W., , Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
- David I. McCooey. . [2022-09-07]. (原始内容存档于2022-09-10).
- . qfbox.info. [2022-09-08]. (原始内容存档于2022-12-31).
- . polyhedra.tessera.li. [2022-09-10]. (原始内容存档于2022-09-10).
- Rajwade, A.R. . Texts and Readings in Mathematics. Hindustan Book Agency. 2001. ISBN 9789386279064.
- Richard Klitzing. . bendwavy.org. [2022-09-08]. (原始内容存档于2022-11-14).
