克拉梅爾猜想
關於質數間隙的條件結果
克拉梅爾也提出另一個較弱的關於素数間隙的猜想,指出在黎曼猜想成立的狀況下,有
- 。[1]
目前這方面最好的無條件結果是
而這點由Baker、Harman和Pintz三人證出。[2]
另一方面E. Westzynthius於1931年證明說質數間隙成長速度快過對數,也就是說,[3]
R. A. Rankin改進了他的結果,[4]並證明說
艾狄胥·帕爾猜想說上式的左側趨近於無限,而這點於2014年由Kevin Ford、Ben Green、Sergei Konyagin和陶哲軒四人組。[5]以及詹姆斯·梅納德分別證出。[6]這兩組人馬在該年稍晚將這結果以這因子進行改進。[7]
探索性論證
克拉梅爾猜想是基於本質上探索性的機率模型之上的,在其中一個大小為x的數是質數的機率是。而這結果又稱作「克拉梅爾隨機模型」(Cramér random model)或「克拉梅爾質數模型」(Cramér model of the primes)。[8]
然而,Andrew Granville指出,[9]根據邁爾定理,克拉梅爾隨機模型不能適切地描述質數在短區間上的分布,而在考慮可除性後,修正版克拉梅爾模型指向(A125313),其中是歐拉-馬斯刻若尼常數。János Pintz則認為這比值的上極限可能發散至無限;[10]
類似地,Leonard Adleman和Kevin McCurley寫道說:
- 「由於H. Maier關於相鄰質數間隙的工作之故,學界對克拉梅爾猜想的確實公式起了疑問…(中略)因此很有可能對於任意的常數而言,總存在一個常數,使得和有一個質數。」[11]
類似地,Robin Visser寫道說:
- 「事實上,由於Granville的工作之故,現在學界普遍相信說克拉梅爾猜想是錯的。實際上也確實有邁爾定理等關於短區間的定理,和克拉梅爾模型難以兼容。」[12]
相關猜想和探索
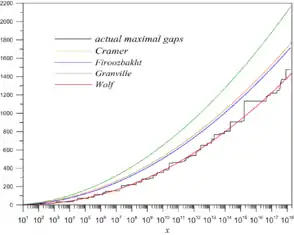
Daniel Shanks猜想說對質數間隙而言,下列比克拉梅爾猜想來得強的非病態公式成立:[13]
J.H. Cadwell[14]則提出下列何質數間隙有關的公式: 這公式和Shanks猜想在形式上一致,但同時提出了低次項。
Marek Wolf[15]則猜想說在以素數計數函數表示的狀況下,最大質數間隙如下:
其中和是孿生質數常數的兩倍,可見A005597和A114907的相關內容。再一次地,這公式和Shanks猜想在形式上一致,但同時提出了如下的低次項:
Thomas Nicely(發現奔騰浮點除錯誤的數學家)曾對許多大質數間隙進行計算,[16]他藉由下列公式來計算質數間隙與克拉梅爾猜想相契合的程度:
他寫道說「即使對於已知最大的質數間隙,的值都維持在1.13左右。」
參見
- 質數定理
- 勒讓德猜想和Andrica猜想─兩個遠遠較弱但依舊未證出的關於質數間隙上界的猜想。
- Firoozbakht猜想
- 邁爾定理─一個關於短區間質數個數且克拉梅爾模型給出錯誤預測的定理。
參考資料
- Cramér, Harald, (PDF), Acta Arithmetica, 1936, 2: 23–46 [2012-03-12], doi:10.4064/aa-2-1-23-46, (原始内容 (PDF)存档于2018-07-23)
- R. C. Baker, G. Harman, and J. Pintz, The difference between consecutive primes. II. Proc. London Math. Soc. (3), 83 (2001), no. 3, 532-562
- Westzynthius, E., , Commentationes Physico-Mathematicae Helsingsfors, 1931, 5: 1–37, JFM 57.0186.02, Zbl 0003.24601 (德语).
- R. A. Rankin, The difference between consecutive prime numbers, J. London Math. Soc. 13 (1938), 242-247
- Ford, Kevin; Green, Ben; Konyagin, Sergei; Tao, Terence. . Annals of Mathematics. Second series. 2016, 183 (3): 935–974. arXiv:1408.4505
 . doi:10.4007/annals.2016.183.3.4
. doi:10.4007/annals.2016.183.3.4  .
. - Maynard, James. . Annals of Mathematics. Second series. 2016, 183 (3): 915–933. arXiv:1408.5110
 . doi:10.4007/annals.2016.183.3.3
. doi:10.4007/annals.2016.183.3.3  .
. - Ford, Kevin; Green, Ben; Konyagin, Sergei; Maynard, James; Tao, Terence. . Journal of the American Mathematical Society. 2018, 31: 65–105. arXiv:1412.5029
 . doi:10.1090/jams/876.
. doi:10.1090/jams/876. - Terry Tao, 254A, Supplement 4: Probabilistic models and heuristics for the primes (optional), section on The Cramér random model, January 2015.
- Granville, A., (PDF), Scandinavian Actuarial Journal, 1995, 1: 12–28 [2007-06-05], doi:10.1080/03461238.1995.10413946, (原始内容 (PDF)存档于2015-09-23).
- János Pintz, Very large gaps between consecutive primes, Journal of Number Theory 63:2 (April 1997), pp. 286–301.
- Leonard Adleman and Kevin McCurley, Open Problems in Number Theoretic Complexity, II. Algorithmic number theory (Ithaca, NY, 1994), 291–322, Lecture Notes in Comput. Sci., 877, Springer, Berlin, 1994.
- Robin Visser, Large Gaps Between Primes, University of Cambridge (2020).
- Shanks, Daniel, , Mathematics of Computation (American Mathematical Society), 1964, 18 (88): 646–651, JSTOR 2002951, Zbl 0128.04203, doi:10.2307/2002951
 .
. - Cadwell, J. H., , Mathematics of Computation, 1971, 25 (116): 909–913, JSTOR 2004355, doi:10.2307/2004355

- Wolf, Marek, , Phys. Rev. E, 2014, 89 (2): 022922, Bibcode:2014PhRvE..89b2922W, PMID 25353560, S2CID 25003349, arXiv:1212.3841
 , doi:10.1103/physreve.89.022922
, doi:10.1103/physreve.89.022922 - Nicely, Thomas R., , Mathematics of Computation, 1999, 68 (227): 1311–1315, Bibcode:1999MaCom..68.1311N, MR 1627813, doi:10.1090/S0025-5718-99-01065-0
 .
.
- Guy, Richard K. 3rd. Springer-Verlag. 2004. A8. ISBN 978-0-387-20860-2. Zbl 1058.11001.
- Pintz, János. . Functiones et Approximatio Commentarii Mathematici. 2007, 37 (2): 361–376. ISSN 0208-6573. MR 2363833. Zbl 1226.11096. doi:10.7169/facm/1229619660
 .
. - Soundararajan, K. . Granville, Andrew; Rudnick, Zeév (编). . NATO Science Series II: Mathematics, Physics and Chemistry 237. Dordrecht: Springer-Verlag. 2007: 59–83. ISBN 978-1-4020-5403-7. Zbl 1141.11043.