列維-奇維塔符號

在二維中，列維-奇維塔符號定義如下：

${\displaystyle \varepsilon _{ij}={\begin{cases}+1\\-1\\0\end{cases}}\,}$	當 ${\displaystyle \left(i,j\right)=\left(1,2\right)}$
	當 ${\displaystyle \left(i,j\right)=\left(2,1\right)}$
	當 ${\displaystyle i=j}$

這些值可以排列成 2×2 反對稱矩陣：

${\displaystyle {\begin{pmatrix}\varepsilon _{11}&\varepsilon _{12}\\\varepsilon _{21}&\varepsilon _{22}\end{pmatrix}}={\begin{pmatrix}0&1\\-1&0\end{pmatrix}}}$

相對於其他維度，二維的列維-奇維塔符號並不常見，雖然在某些專門的主題，如超對稱和扭量理論中，談及2-旋量時會用到。

對於 ε_ijk 的指標 (i, j, k) ，數字 1, 2, 3 在   循環排列的次序，對應 ε = +1。在   反循環排列的次序，則對應 ε = −1。其餘情況下， ε = 0。

三維以上的列維-奇維塔符號更常用。在三維中，列維-奇維塔符號定義如下：

${\displaystyle \varepsilon _{ijk}={\begin{cases}+1\\-1\\0\end{cases}}\,}$	當 ${\displaystyle \left(i,j,k\right)=\left(1,2,3\right)}$ 、 ${\displaystyle \left(2,3,1\right)}$ 或 ${\displaystyle \left(3,1,2\right)}$
	當 ${\displaystyle \left(i,j,k\right)=\left(3,2,1\right)}$ 、 ${\displaystyle \left(2,1,3\right)}$ 或 ${\displaystyle \left(1,3,2\right)}$
	當 ${\displaystyle i=j}$ 、 ${\displaystyle j=k}$ 或 ${\displaystyle i=k}$

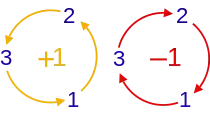
也就是說，如果 (i, j, k) 是 (1, 2, 3) 的偶排列，則符號值為 +1 。如果是奇排列，則符號值為 −1 。如果任何兩個索引重複，則符號值為 0 。

僅在三維中， (1, 2, 3) 的循環排列都是偶排列，反循環排列都是奇排列。這意味著在三維中，僅觀察 (i, j, k) 是 (1, 2, 3) 的循環排列，還是反循環排列，就足以分辨其奇偶性。

類似於二維矩陣，三維列維-奇維塔符號的值可以排成 3×3×3 陣列：

其中 i 是深度 (藍色: i = 1; 紅色: i = 2; 綠色: i = 3) ， j 是橫行，k 是直列。

以下是一些例子：

${\displaystyle {\begin{aligned}\varepsilon _{\color {BrickRed}{1}\color {Violet}{3}\color {Orange}{2}}=-\varepsilon _{\color {BrickRed}{1}\color {Orange}{2}\color {Violet}{3}}&=-1\\\varepsilon _{\color {Violet}{3}\color {BrickRed}{1}\color {Orange}{2}}=-\varepsilon _{\color {Orange}{2}\color {BrickRed}{1}\color {Violet}{3}}&=-(-\varepsilon _{\color {BrickRed}{1}\color {Orange}{2}\color {Violet}{3}})=1\\\varepsilon _{\color {Orange}{2}\color {Violet}{3}\color {BrickRed}{1}}=-\varepsilon _{\color {BrickRed}{1}\color {Violet}{3}\color {Orange}{2}}&=-(-\varepsilon _{\color {BrickRed}{1}\color {Orange}{2}\color {Violet}{3}})=1\\\varepsilon _{\color {Orange}{2}\color {Violet}{3}\color {Orange}{2}}=-\varepsilon _{\color {Orange}{2}\color {Violet}{3}\color {Orange}{2}}&=0\end{aligned}}}$

在四維中，列維-奇維塔符號定義如下：

${\displaystyle \varepsilon _{ijkl}={\begin{cases}+1\\-1\\0\end{cases}}\,}$	當 ${\displaystyle \left(i,j,k,l\right)=\left(1,2,3,4\right)}$ 的偶排列
	當 ${\displaystyle \left(i,j,k,l\right)=\left(1,2,3,4\right)}$ 的奇排列
	其餘情況，即任意兩個指標相等

這些值可以排成 4×4×4×4 陣列，然而四維以上較難描繪出示意圖。

以下是一些例子：

${\displaystyle {\begin{aligned}\varepsilon _{\color {BrickRed}{1}\color {RedViolet}{4}\color {Violet}{3}\color {Orange}{\color {Orange}{2}}}=-\varepsilon _{\color {BrickRed}{1}\color {Orange}{\color {Orange}{2}}\color {Violet}{3}\color {RedViolet}{4}}&=-1\\\varepsilon _{\color {Orange}{\color {Orange}{2}}\color {BrickRed}{1}\color {Violet}{3}\color {RedViolet}{4}}=-\varepsilon _{\color {BrickRed}{1}\color {Orange}{\color {Orange}{2}}\color {Violet}{3}\color {RedViolet}{4}}&=-1\\\varepsilon _{\color {RedViolet}{4}\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {BrickRed}{1}}=-\varepsilon _{\color {BrickRed}{1}\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {RedViolet}{4}}&=-(-\varepsilon _{\color {BrickRed}{1}\color {Orange}{\color {Orange}{2}}\color {Violet}{3}\color {RedViolet}{4}})=1\\\varepsilon _{\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {RedViolet}{4}\color {Violet}{3}}=-\varepsilon _{\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {RedViolet}{4}\color {Violet}{3}}&=0\end{aligned}}}$

更一般地推廣到 n 維中，則列維-奇維塔符號的定義為：

${\displaystyle \varepsilon _{a_{1}a_{2}a_{3}\ldots a_{n}}={\begin{cases}+1\\-1\\0\end{cases}}}$	當 ${\displaystyle (a_{1},a_{2},a_{3},\ldots ,a_{n})}$ 是 ${\displaystyle (1,2,3,\dots ,n)}$ 的偶排列
	當 ${\displaystyle (a_{1},a_{2},a_{3},\ldots ,a_{n})}$ 是 ${\displaystyle (1,2,3,\dots ,n)}$ 的奇排列
	其餘情況，即任意兩個指標相等

又可使用求積符號 ∏ 表達為：

${\displaystyle {\begin{aligned}\varepsilon _{a_{1}a_{2}a_{3}\ldots a_{n}}&=\prod _{1\leq i<j\leq n}\operatorname {sgn}(a_{j}-a_{i})\\&=\operatorname {sgn}(a_{2}-a_{1})\operatorname {sgn}(a_{3}-a_{1})\dots \operatorname {sgn}(a_{n}-a_{1})\operatorname {sgn}(a_{3}-a_{2})\operatorname {sgn}(a_{4}-a_{2})\dots \operatorname {sgn}(a_{n}-a_{2})\dots \operatorname {sgn}(a_{n}-a_{n-1})\end{aligned}}}$

其中的 sgn(x) 是符號函數，根據 x 的正負給出 +1 、 0 或 −1。該公式對對於任何 n 及任何指標排列都有效（當 n = 0 或 1 時，定義為空積 1）。

然而，計算以上公式的時間複雜度為 O(n²) ，而以不交循環排列的性質計算，則只需 O(n log(n)) 。

兩個列維-奇維塔符號的積，可以用一個以廣義克羅內克函數表示的行列式求得：

${\displaystyle \varepsilon _{ijk\dots }\varepsilon _{mnl\dots }={\begin{vmatrix}\delta _{im}&\delta _{in}&\delta _{il}&\dots \\\delta _{jm}&\delta _{jn}&\delta _{jl}&\dots \\\delta _{km}&\delta _{kn}&\delta _{kl}&\dots \\\vdots &\vdots &\vdots \\\end{vmatrix}}}$

在线性代数中， 3×3 的方陣 A = (a_ij) ：

${\displaystyle A={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}}}$，

其行列式可以寫為：

${\displaystyle \det(A)=\sum _{i,j,k=1}^{3}\varepsilon _{ijk}\,a_{1i}\,a_{2j}\,a_{3k}}$，

類似地， n×n 矩陣 A = (a_ij) 的行列式可以寫為：

${\displaystyle \det(A)=\sum _{a_{1},a_{2},\cdots ,a_{n}=1}^{n}\varepsilon _{a_{1}a_{2}\cdots a_{n}}\,a_{1a_{1}}\,a_{2a_{2}}\,\cdots \,a_{na_{n}},}$

對於向量 a 與 b ，它們的叉積：

${\displaystyle {\boldsymbol {a}}\times {\boldsymbol {b}}={\begin{vmatrix}{\boldsymbol {e}}_{1}&{\boldsymbol {e}}_{2}&{\boldsymbol {e}}_{3}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{vmatrix}}=\sum _{1\leq i,j,k\leq 3}\varepsilon _{ijk}\,a_{i}b_{j}\,{\boldsymbol {e}}_{k}}$

對於向量 a 、 b 與 c ，它們的三重積：

${\displaystyle {\boldsymbol {a}}\cdot ({\boldsymbol {b}}\times {\boldsymbol {c}})={\begin{vmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\\\end{vmatrix}}=\sum _{1\leq i,j,k\leq 3}\varepsilon _{ijk}\,a_{i}b_{j}c_{k}}$

在二維上，當所有${\displaystyle i}$，${\displaystyle j}$，${\displaystyle m}$，${\displaystyle n}$各取值1和2時，

${\displaystyle \varepsilon _{ij}\varepsilon ^{mn}={\delta _{i}}^{m}{\delta _{j}}^{n}-{\delta _{i}}^{n}{\delta _{j}}^{m}}$

(1)

${\displaystyle \varepsilon _{ij}\varepsilon ^{in}={\delta _{j}}^{n}}$

(2)

${\displaystyle \varepsilon _{ij}\varepsilon ^{ij}=2.}$

(3)

在三維中，當所有${\displaystyle i}$，${\displaystyle j}$，${\displaystyle k}$，${\displaystyle m}$，${\displaystyle n}$各取值1,2和3時：

${\displaystyle \varepsilon _{ijk}\varepsilon ^{imn}=\delta _{j}{}^{m}\delta _{k}{}^{n}-\delta _{j}{}^{n}\delta _{k}{}^{m}}$

(4)

${\displaystyle \varepsilon _{jmn}\varepsilon ^{imn}=2{\delta _{j}}^{i}}$

(5)

${\displaystyle \varepsilon _{ijk}\varepsilon ^{ijk}=6.}$

(6)

列維-奇維塔符號與克罗内克函数有關。 在三維中，關係由以下等式給出（垂直線表示行列式）：

${\displaystyle {\begin{aligned}\varepsilon _{ijk}\varepsilon _{lmn}&={\begin{vmatrix}\delta _{il}&\delta _{im}&\delta _{in}\\\delta _{jl}&\delta _{jm}&\delta _{jn}\\\delta _{kl}&\delta _{km}&\delta _{kn}\\\end{vmatrix}}\\[6pt]&=\delta _{il}\left(\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}\right)-\delta _{im}\left(\delta _{jl}\delta _{kn}-\delta _{jn}\delta _{kl}\right)+\delta _{in}\left(\delta _{jl}\delta _{km}-\delta _{jm}\delta _{kl}\right).\end{aligned}}}$

這個結果的一個特例是(4):

${\displaystyle \sum _{i=1}^{3}\varepsilon _{ijk}\varepsilon _{imn}=\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}}$

有時候其被稱為“contracted epsilon identity”。

在愛因斯坦標記法中，${\displaystyle i}$指標的重複表示對於${\displaystyle i}$的求和。由此，上述結論可表記為：

${\displaystyle \varepsilon _{ijk}\varepsilon _{imn}=\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}}$

進一步可以知道：

${\displaystyle \sum _{i=1}^{3}\sum _{j=1}^{3}\varepsilon _{ijk}\varepsilon _{ijn}=2\delta _{kn}}$

在n維中，當所有${\displaystyle i_{1},\ldots ,i_{n},j_{1},\ldots ,j_{n}}$take values${\displaystyle 1,2,\ldots ,n}$：

${\displaystyle \varepsilon _{i_{1}\dots i_{n}}\varepsilon ^{j_{1}\dots j_{n}}=n!\delta _{[i_{1}}^{j_{1}}\dots \delta _{i_{n}]}^{j_{n}}=\delta _{i_{1}\dots i_{n}}^{j_{1}\dots j_{n}}}$

(7)

${\displaystyle \varepsilon _{i_{1}\dots i_{k}~i_{k+1}\dots i_{n}}\varepsilon ^{i_{1}\dots i_{k}~j_{k+1}\dots j_{n}}=k!(n-k)!~\delta _{[i_{k+1}}^{j_{k+1}}\dots \delta _{i_{n}]}^{j_{n}}=k!~\delta _{i_{k+1}\dots i_{n}}^{j_{k+1}\dots j_{n}}}$

(8)

${\displaystyle \varepsilon _{i_{1}\dots i_{n}}\varepsilon ^{i_{1}\dots i_{n}}=n!}$

(9)

驚嘆號(${\displaystyle$ !} )代表階乘，而${\displaystyle \delta _{\beta \ldots }^{\alpha \ldots }}$是廣義克罗内克函数，對於任意n有屬性：

${\displaystyle \sum _{i,j,k,\dots =1}^{n}\varepsilon _{ijk\dots }\varepsilon _{ijk\dots }=n!}$

從以下事實可得出：

• 每個排列是偶排列或奇排列，
• ${\displaystyle (+1)^{2}=(-1)^{2}=1}$，與
• 任何n-元素集合的排列數正好是${\displaystyle n!}$。

一般來說，對於n維，兩個列維-奇維塔符號的乘積可以寫成：

${\displaystyle \varepsilon _{i_{1}i_{2}\dots i_{n}}\varepsilon _{j_{1}j_{2}\dots j_{n}}={\begin{vmatrix}\delta _{i_{1}j_{1}}&\delta _{i_{1}j_{2}}&\dots &\delta _{i_{1}j_{n}}\\\delta _{i_{2}j_{1}}&\delta _{i_{2}j_{2}}&\dots &\delta _{i_{2}j_{n}}\\\vdots &\vdots &\ddots &\vdots \\\delta _{i_{n}j_{1}}&\delta _{i_{n}j_{2}}&\dots &\delta _{i_{n}j_{n}}\\\end{vmatrix}}}$