雙縫實驗
在量子力學裏,雙縫實驗,或稱雙狹縫實驗(英語:)是一種展示光子或電子等微觀物體的波動性與粒子性的實驗。雙縫實驗是一種「雙路徑實驗」。在雙路徑實驗裏,微觀物體可以同時通過兩條路徑或通過其中任意一條路徑,從初始點抵達最終點。這兩條路徑的程差促使描述微觀物體物理行為的量子態發生相移,因此產生干涉現象。另一種常見的雙路徑實驗是马赫-曾德尔干涉仪實驗。

| 系列条目 |
| 量子力学 |
|---|
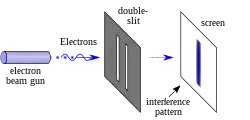
雙縫實驗的基本儀器設置很簡單,如图所示,將像激光一類的相干光束照射到一塊刻有兩條狹縫的不透明板,通過狹縫的光束會抵達照相膠片或某種探測屏,從記錄於照相膠片或某種探測屏的輻照度數據,可以分析光的物理性質。光的波動性使得通過兩條狹縫的光束互相干涉,形成了顯示於探測屏的明亮條紋和暗淡條紋相間的圖樣,明亮條紋是相長干涉區域,暗淡條紋是相消干涉區域,這就是雙縫實驗著名的干涉圖樣。[1]:38-60
在古典力學裏,雙縫實驗又稱為「楊氏雙縫實驗」,或「楊氏實驗」、「楊氏雙狹縫干涉實驗」,專門演示光波的干涉行為,是因物理學者托馬斯·楊而命名。假若光束是以粒子的形式從光源移動至探測屏,抵達探測屏任意位置的粒子數目,應該等於之前通過左狹縫的粒子數量與之前通過右狹縫的粒子數量的總和。根據定域性原理(principle of locality),關閉左狹縫不應該影響粒子通過右狹縫的行為,反之亦然,[2]:7因此,在探測屏的任意位置,兩條狹縫都不關閉的輻照度應該等於只關閉左狹縫後的輻照度與只關閉右狹縫後的輻照度的總和。但是,當兩條狹縫都不關閉時,結果並不是這樣,探測屏的某些區域會比較明亮,某些區域會比較暗淡,這種圖樣只能用光波動說的相長干涉和相消干涉來解釋,而不是用光微粒說的簡單數量相加法。[1]:38-60
雙縫實驗也可以用來檢試像中子、原子等微觀物體的物理行為,雖然使用的儀器不同,但仍舊會得到類似的結果。每一個單獨微觀物體都離散地撞擊到探測屏,撞擊位置無法被預測,演示出整個過程的機率性,累積很多撞擊事件後,總體又顯示出干涉圖樣,演示微觀物體的波動性。[1]:38-60[2]:8-9
2013年,一個檢試分子物理行為的雙縫實驗成功演示出含有810個原子、質量約為10,000amu的分子也具有波動性。[3]
理查德·費曼在著作《費曼物理學講義》裏表示,雙縫實驗所展示出的量子現象不可能、絕對不可能以任何古典方式來解釋,它包含了量子力學的核心思想。事實上,它包含了量子力學唯一的奧秘[1]:39。透過雙縫實驗,可以觀察到量子世界的奧秘。
概述

.jpg.webp)
假若光束是由古典粒子組成,將光束照射於一條狹縫,通過狹縫後,衝擊於探測屏,則在探射屏應該會觀察到對應於狹縫尺寸與形狀的圖樣。可是,實際進行這單縫實驗時,探測屏會顯示出衍射圖樣,光束會被展開,狹縫越狹窄,則展開角度越大。如右圖所示,在探測屏會顯示出,在中央區域有一塊比較明亮的光帶,旁邊襯托著兩塊比較暗淡的光帶。[1]:38-60
類似地,假若光束是由古典粒子組成,將光束照射於兩條相互平行的狹縫,則在探射屏應該會觀察到兩個單縫圖樣的總和。但實際並不是這樣,如右圖所示,在探射屏顯示出一系列明亮條紋與暗淡條紋相間的圖樣。 19世紀初,托馬斯·楊發表了一篇論文,《物理光學的相關實驗與計算》(Experiments and Calculations Relative to Physical Optics),詳細闡述這些實驗結果。由於亮度分佈可以用波的相長干涉與相消干涉這兩種干涉機制來解釋,意味著光是一種振動波,這促使光波動說被廣泛接受,也導致17、18世紀的主流理論─光微粒說─漸趨式微。但是後來20世紀初對於光電效應的理論突破演示出,在不同狀況,光的物理行為可以解釋為光是由粒子組成。這些貌似相互矛盾的發現,使得物理學家必須想辦法超越古典力學,更仔細地將光的量子性質納入考量。[4]
使用雙縫實驗與各種不同衍生的變版來檢試單獨粒子的物理行為,這方法已成為經典的思想實驗,因為它能夠清楚地探討量子力學的核心謎題,它演示出對於實驗結果的理論預測能力所不可避免的基礎極限[1]:38-60。
例如,稍微改變雙縫實驗的設計,在狹縫後面裝置探測器,專門探測光子通過的是哪一條狹縫,則干涉圖樣會完全消失,不再能觀察到干涉圖樣;替代顯示出的是兩個單縫圖樣的簡單總和。這種反直覺而又容易製成的結果,使得物理學者感到非常困惑不解。帢斯拉夫·布魯克納(Časlav Brukner)與安東·蔡林格精簡地表示如下:[5]
觀察者可以決定是否裝置探測器於光子的路徑。從決定是否探測雙縫實驗的路徑,他可以決定哪種性質成為物理實在。假若他選擇不裝置探測器,則干涉圖樣會成為物理實在;假若他選擇裝置探測器,則路徑信息會成為物理實在。然而,更重要地,對於成為物理實在的世界裡的任何特定元素,觀察者不具有任何影響。具體而言,雖然他能夠選擇探測路徑信息,他並無法改變光子通過的狹縫是左狹縫還是右狹縫,他只能從實驗數據得知這結果。類似地,雖然他可以選擇觀察干涉圖樣,他並無法操控粒子會衝擊到探測屏的哪個位置。兩種結果都是完全隨機的。
尚未特別加以處理的光束是由很多光子組成的,為了要進一步了解雙縫實驗的物理行為,物理學者好奇地問,假設光子是一個一個的通過狹縫,那麼,會出現甚麼物理狀況?[6]1909 年,為了解答這問題,傑弗里·泰勒爵士設計並且完成了一個很精緻的雙縫實驗[7]。這實驗將入射光束的強度大大降低,在任何時間間隔內,平均最多只有一個光子被發射出來。經過很久時間,累積許多光子於攝影膠片後,他發現,仍舊會出現類似的干涉圖樣。很清楚地,這意味著,雖然每次只有一個光子通過狹縫,這光子可以同時通過兩條狹縫,自己與自己互相干涉![註 1]類似地,電子、中子、原子、甚至分子,都可以表現出這種奇異的量子行為[2]:8-9。
1961年,蒂賓根大學的克劳斯·约恩松()創先地用雙縫實驗來檢試電子的物理行為,他發現電子也會發生干涉現象[11][12]。1974年,皮尔·梅利() ,在米蘭大學的物理實驗室裏,成功的將電子一粒一粒的發射出來。在探測屏上,他也明確地觀察到干涉現象。2002年9月,约恩松的雙縫實驗,被《Physics World》雜誌的讀者,選為最美麗的物理實驗[13]。
光波動說和光微粒說

以光波動說來解釋光的干涉,光波的兩個波前同時地從兩個狹縫以同心圓圖案傳播出去。在探測屏的任意位置,兩個光波的疊加,決定了那位置被觀測到的強度。在探測屏上觀察到的明亮的條紋,是由兩個光波的相長干涉造成的,當一個波峰遇到另外一個波峰時,會產生相長干涉。暗淡的條紋是由光波的相消干涉造成的,當一個波峰遇到另外一個波谷時,會產生相消干涉。[14]:48-51
以光微粒說來解釋,光子的量子行為可以用機率波來描述,機率波的兩個波前同時地從兩個狹縫以同心圓圖案傳播出去。在探測屏的任意位置,兩個機率波的疊加,決定了光子會移動到那位置的機率密度。更詳細地說,兩個機率波的機率幅相加後,取絕對值平方,就是在那位置找到光子的機率密度。經過累積許多光子後,可以在探測屏觀察到一系列明亮條紋與暗淡條紋相間的圖樣。[14]:48-51
雙縫實驗的變版
單獨粒子的干涉現象
隨著科技的進步,現在已發展出能可靠地發射單獨電子的物理儀器。使用這種單獨電子發射器來進行雙縫實驗,可以使得在任意時間最多只有一個電子存在於發射器與探測屏之間,因此,每一次最多只有一個電子通過雙狹縫,而不是一大群電子在很短時間間隔內擠著要通過雙狹縫。值得注意的是,如右圖所示,探測屏累積很多次電子衝擊事件之後,會顯示出熟悉的干涉圖樣。從這圖樣可以推論,單獨電子似乎可以同一時刻通過兩條狹縫,並且自己與自己干涉[14]:110[註 1]。這解釋並不符合平常觀察到的離散物體的物理行為,人們從未親眼目睹老虎在同時刻穿越兩個並排的火圈,這並不是很容易從直覺就能夠讚同的結果。可是,從原子到更複雜的分子,包括巴基球,這些微觀粒子都會產生類似現象[17][18]。
不論是電子、中子或是任何其它量子尺寸的粒子,在雙縫實驗裏,粒子抵達探測屏的位置的機率分佈具有高度的決定性。量子力學可以精確地預測粒子抵達探測屏任意位置的機率密度,可是,量子力學無法預測在什麼時刻、在探測屏的什麼位置,會有一個粒子抵達。這無可爭議的結果,是經過多次重複的實驗而得到的。這結果帶給科學家極大的困惑,因為無法預測粒子的抵達位置,這意味著沒有任何緣由而發生的粒子的抵達事件。很多物理學者非常不願意接受的這個事實。[19]:204-213。儘管量子力學可以正確地預測實驗結果,但量子力學不能解釋為何會發生這種現象,為甚麼粒子似乎可以同時通過兩條狹縫?答:﹝因為波粒二象性的解釋,電子既是粒子也是波動,電子在兩個狹縫會同時有機率存在﹞。阿爾伯特·愛因斯坦認為,從這裡可以推論出量子力學並不完備,一個完備的理論必須對這些難題給出滿意解釋。尼爾斯·玻爾反駁,這正好顯示出量子力學的優點,量子力學不會用不恰當的古典概念來解釋這種量子現象,如果必要,量子力學可以尋找與應用新的概念來解釋這些難題[2]:18-21。
探測路徑信息
試想一個思想實驗,假設裝置探測器來觀察光子到底是從那一條狹縫經過,因此能夠獲得路徑信息(不論是否真正讀取這路徑信息),則干涉圖樣會消失[1]:38-60。這種路徑實驗演示出粒子性與波動性的互補原理,光子可以表現出粒子性,也可以表現出波動性,但不能同時表現出粒子性與波動性[20][21]。雖然這思想實驗對於量子力學的基礎理論極為重要,但直到1970年代也沒有出現任何可能的技術體現這思想實驗的提議。實際而言,這類實驗也無法簡單地設置,因為舊式探測器會將光子吸收[22]。但現今,已完成多個實驗展示關於互補性的各各方面,例如量子擦除實驗[23]。
於1987年完成的一個實驗發現了一個驚人的結果,假若只獲得部分路徑信息,則干涉圖樣不會完全消失。這實驗顯示,假若測量的動作不過度攪擾粒子的運動,則干涉圖樣也只會對應地被改變[24]。在恩格勒-格林柏格對偶關係式,有對於這方面量子行為的詳細數學論述。
量子擦除實驗
量子擦除實驗與延遲選擇實驗是雙縫實驗更為進階的變版,能夠演示更多量子力學的特色。
量子擦除實驗演示,藉著擦除路徑信息,可以恢復波動行為所產生的干涉圖樣。這實驗有三個步驟:[25]
- 照射粒子束於刻有兩條狹縫的不透明板,然後確認在探測屏出現了干涉圖樣。
- 觀察粒子通過的是哪條狹縫,在觀察時,必須小心翼翼地不過度攪擾光子的運動[註 3],然後,證實顯示於探測屏的干涉圖樣已被消毀。這步驟演示出,干涉圖樣是因為有可能獲得路徑信息而被消毀。
- 通過特別程序,可以將路徑信息擦除,但也可重新得到干涉圖樣。
延遲選擇實驗演示,在粒子抵達探測屏之後,可以藉著擦除或標記路徑信息,恢復或摧毀干涉圖樣。這種時間差距關係,理論上甚至可以拉長至非常長久。假若標記路徑信息,則粒子只通過了一條路徑;假若擦除路徑信息,則粒子同時通過了兩條路徑。這意味著,觀察者現在的行為可以決定過去發生的事,而這一結論是與傳統實在觀相違背的。[25]
其它種變版
1967年,傅立誥(R. Pfleegor)與曼德爾(L. Mandel)完成實驗演示,使用兩個激光源,可以產生「雙源干涉」,假若探測器獲得光子是從哪個激光器發射出來的路徑信息,則在探測屏不會顯示出干涉圖樣;假若不存在路徑信息,則在探測屏會顯示出干涉圖樣。這意味著當探測屏顯示出干涉圖樣時,無法得知光子的發射源是哪個激光器[2]:50-52[26]。
1972年,理查德·西利托與凱瑟琳·威克斯(Catherine Wykes)將雙縫實驗做修改,在任何時間,只有一條狹縫是開放的,另外一條狹縫是關閉的。參予干涉作用的光子的平均密度超小於 1 ,在任何時間,光子只能經過兩條狹縫中的一條狹縫。雖然如此,假若路徑程差允許抵達探測屏的光子可以來自任意一條狹縫,干涉圖樣仍舊能被觀察到.[27]。
近幾年來的科學研究,更進一步地發現了,干涉現象並不只限制於像質子、中子、電子等等基本粒子。用雙縫實驗檢試大分子構造,像富勒烯 ( ) ,也能夠產生類似的干涉圖樣[28]。
2012年,內布拉斯加大學林肯分校的物理系研究團隊實現了理查·費曼所描述的雙縫思想實驗。[註 4]該實驗使用最新儀器,可以隨意控制每一條真正狹縫的關閉與開放。該實驗檢試電子在以下三種狀況所出現的物理行為:第一條狹縫開放與第二條狹縫關閉、第一條狹縫關閉與第二條狹縫開放、兩條狹縫都開放。實驗結果符合量子力學的量子疊加原理,演示出電子的波動性。該實驗還實際探測到電子一個一個的抵達探測屏,演示出電子的粒子性[29][註 2]。
古典波動光學表述


克裡斯蒂安·惠更斯提出惠更斯原理表明,波前的每一點可以認為是產生球面次波的點波源,而以後任何時刻的波前則可看作是這些次波的包絡,這是光波傳播的基本原理,可以預測光波在介質中的傳播。從光源釋出一連串的光波,就好似浮在水面上的浮標,被重複的拉起來,放下去,製成了水波在水面傳播。惠更斯想出一種預測波前位置的方法,如右圖所示,繪製一組圓心包含於一個波前的同半徑圓圈,它們的切線,經過連接與平滑後,形成一條連續的曲線,這就是預測的波前位置。依照這方法,可以展示出一個平面波波前或一個圓形波波前怎樣持續延伸。將惠更斯原理加以數學論述,奧古斯丁·菲涅耳證明光波動說與光在介質內以直線傳播的射線行為相符合,不存在任何矛盾之處。菲涅耳又對於繞射與干涉現象,給出一個合理、完整的解釋。[6]更詳盡細節,請參閱惠更斯-菲涅耳原理。
如右圖所示 ,在任何時刻,用一個波前來代表那時刻所有從光源 傳播出來的光波。通過兩條狹縫後,波前衍散出來,在探測屏形成的干涉圖樣中,任何兩個位置的距離 ,會隨著不透明板與探測屏的距離 而變;假若 增加,則 也增加;減小兩條狹縫 , 之間的距離 ,會增加條紋之間的距離;增加光波的波長 ,也會增加條紋之間的距離;狹縫的縫寬的尺寸必須適當,否則,單縫干涉效應會變得很顯著,因此蓋壓過雙縫實驗效應;反過來說,假若狹縫太寬(例如,一座牆上的兩扇普通窗子),則光波會直接投射過去,就觀察不到干涉現象了。[30]:147-155
在探測屏上觀察到的明亮條紋,是由光波的相長干涉造成的,當一個波峰遇到另外一個波峰時,會產生相長干涉;暗淡的條紋是由光波的相消干涉造成的,當一個波峰遇到另外一個波谷時,會產生相消干涉。用方程式表達,當以下關係成立時,會發生相長干涉[30]:147-155:
- ;
其中, 是最大輻照度值(波峰遇到波峰,最大相長干涉的光波輻照度)的次序數(位於中央的最大強度值的次序數是 ), 是條紋與中央之間的距離(稱為條紋距離)[30]:147-155。
這方程式只是一個近似。方程式的成立依賴某些先決條件的成立。應用這方程式於實驗儀器, 和 是實驗參數, 可以由實驗測量得知,有了這幾個數值,就可以計算應該使用哪種波長的光波來製成雙縫干涉。[31]
量子物理中对實驗的詮釋
哥本哈根詮釋
哥本哈根詮釋為許多先驅量子力學學者的共識。哥本哈根詮釋明確地闡明,數學公式和精確實驗給出很多關於原子尺寸的知識,任何大膽假設都不應該超越這些知識範圍。機率波是一種能夠預測某些實驗結果的數學構造。它的數學形式類似物理波動的描述。機率波的機率幅,取其絶對值平方,則可得到可觀測的微觀物理現象發生的機率。應用機率波的概念於雙縫實驗,物理學家可以計算出微觀物體抵達探測屏任意位置的機率。[32]:5-6
除了光子的發射時間與抵達探測屏時間以外,在這兩個時間之間任何其它時間,光子的位置都無法被確定;為了要確定光子的位置,必須以某種方式探測它;可是,一旦探測到光子的位置,光子的量子態也會被改變,干涉圖樣也因此會被影響;所以,在發射時間與抵達探測屏時間之間,光子的位置完全不能被確定。[33]:195-196[34]:3-4
一個光子,從被太陽發射出來的時間,到抵達觀察者的視網膜,引起視網膜的反應的時間,在這兩個時間之間,觀察者完全不知道,發生了什麼關於光子的事。或許這論點並不會很令人驚訝;可是,從雙縫實驗可以推論出一個很值得的結果;假若,用探測器來探測光子會經過兩條狹縫中的那一條狹縫,則原本的干涉圖樣會消失不見;假若又將這探測器所測得路徑信息摧毀,則干涉圖樣又會重現於探測屏(更詳盡內容,請參閱條目量子擦除實驗),這引人思維的現象將雙縫實驗的程序與結果奧妙地連結在一起。[33]:195-196
路徑積分表述
路徑積分表述是理查·費曼提出的一個理論(費曼強調這個表述只是一種數學描述,而並不是嘗試描述某些無法觀察到的真實程序)。路徑積分表述不採用粒子的單獨唯一運動軌道這種古典概念,取而代之的是所有可能軌道的總和。使用泛函積分,可以計算出所有可能軌道的總和。[35]:116-129
路徑積分表述闡明,假設一個光子要從發射點a移動至探測屏的位置點d,它會試著選擇經過所有的可能路徑,包括選擇同時經過兩條狹縫的路徑;可是,假若用探測器,來觀察光子會經過兩條狹縫中的那一條狹縫,整個實驗設置立刻有所改變;假設探測器的位置為點e,而探測器觀察到光子,則新的路徑是從點e到點d;這樣,在點e與點d之間,只有空曠的空間,並沒有兩條狹縫,所以不會出現干涉圖樣。[25][36]:77-82
註釋
- 物理大師保羅·狄拉克主張,每一個光子只與自己相互干涉。不同的光子絕對不會相互干涉。[8]:9但是後來,物理學者做實驗發現,幾個光子也會彼此相互干涉。[9]:14-17[10]
- 雖然每一點表示一個電子抵達探測屏,這事實並不能表現出電子的粒子性,因為探測器是由離散原子組成的,這可以詮釋為電子波與離散原子彼此之間的相互作用,這是探測器的特性,但是探測這動作造成電子波的塌縮。[15]:sec iv
- 根據海森堡不確定性原理,對某粒子進行測量,必定會攪擾到這粒子。
- 外村彰團隊完成的電子雙縫實驗所使用的是雙稜鏡干涉(biprism interference)機制,在兩塊相互平行的接地金屬板之間,置入一條帶正價的細金屬絲,將電子束照射於這設置後,在螢光屏收集抵達電子的相關數據。[16]
參考文獻
- 費曼, 理查; 雷頓, 羅伯; 山德士, 馬修. . 台灣: 天下文化書. 2006. ISBN 986-417-672-2.
- George Greenstein; Arthur Zajonc. . Jones & Bartlett Learning. 2006. ISBN 978-0-7637-2470-2.
- Eibenberger, Sandra; et al. . Physical Chemistry Chemical Physics. 2013, 15: pp. 14696–14700 [2014-01-01]. doi:10.1039/C3CP51500A. (原始内容存档于2021-05-07).
- 愛因斯坦, 阿爾伯特. . New York: Philosophical Library. 1934: pp. 100.
- Brukner C, Zeilinger A. . Philosophical Transactions of the Royal Society. 2002, 360: 1061–1069.
- 德布罗意. . New York: Noonday Press. 1953: pp. 47, 117, 178–186.
- Sir Geoffrey Ingram Taylor, "Interference Fringes with Feeble Light", Proc. Cam. Phil. Soc. 15, 114 (1909)。
- Paul Adrien Maurice Dirac. . Oxford University Press. 1 January 1981. ISBN 978-0-19-852011-5.
- Kurt Gottfried; Tung-Mow Yan. . Springer. 19 June 2003. ISBN 978-0-387-95576-6.
- Kurt, Gottfried. (PDF). American Journal of Physics. Feb 2000, 68 (2): 143–147 [2014-03-08]. (原始内容存档 (PDF)于2014-03-08).
- Jönsson C, Zeitschrift für Physik, 161:454
- Jönsson C (1974). Electron diffraction at multiple slits. American Journal of Physics, 4:4-11
- "The most beautiful experiment" (页面存档备份,存于). Physics World 2002
- Greene, Brian. . New York: W. W. Norton. 1999. ISBN 0393046885.
- Hobson, Art. . American Journal of Physics. 2013, 81 (211) [2014-09-25]. doi:10.1119/1.4789885. (原始内容存档于2015-02-10).
- Tonomura, Akira; et al. (PDF). American Journal of Physics. 1988, 57 (2): 117–120. doi:10.1119/1.16104. (原始内容 (PDF)存档于2014-01-16).
- Olaf Nairz, Björn Brezger, Markus Arndt, and Anton Zeilinger, Abstract, "Diffraction of Complex Molecules by Structures Made of Light (页面存档备份,存于)," Phys. Rev. Lett. 87, 160401 (2001)
- Nairz O, Arndt M, and Zeilinger A. Quantum interference experiments with large molecules 的存檔,存档日期2012-03-24.. American Journal of Physics, 2003; 71:319–325. doi:10.1119/1.1531580
- Greene, Brian. . Knopf. 2004. ISBN 0375412883.
- Cassidy, David. . Werner Heisenberg. American Institute of Physics. 2008 [2009-04-14]. (原始内容存档于2016-01-14).
- Boscá Díaz-Pintado, María C. . . Leeds, UK. 29–31 March 2007 [2009-04-14]. (原始内容存档于2010-07-01).
- Bartell, L. S. . Physical Review D. 1980, 21 (6): 1698–1699. doi:10.1103/physrevd.21.1698.
- Zeilinger, Anton. . Reviews of Modern Physics. 1999, 71 (2): S288–S297 [2018-03-03]. doi:10.1103/revmodphys.71.s288. (原始内容存档于2021-02-18).
- P. Mittelstaedt, A. Prieur and R. Schieder, Unsharp particle-wave duality in a photon split-beam experiment, Foundations of Physics 17, 891-903 (1987)
- Walborn, S . P.; et al.. . Phys. Rev. A. 2002, 65 (3): 033818 [2014-01-15]. doi:10.1103/PhysRevA.65.033818. (原始内容存档于2013-11-27).
- Pfleegor, R. L. and Mandel, L. . Physical Review. July 1967, 159 (5): 1084–1088. Bibcode:1967PhRv..159.1084P. doi:10.1103/PhysRev.159.1084.
- Sillitto, R.M. and Wykes, Catherine. . Physics Letters A. 1972, 39 (4): 333–334 [2014-01-15]. Bibcode:1972PhLA...39..333S. doi:10.1016/0375-9601(72)91015-8. (原始内容存档于2014-08-14).
- Nairz O., Arndt M., and Zeilenger A., Quantum interference experiments with large molecules. American Journal of Physics, 2003; 71:319-325.
- Bach, Roger; et al. . New Journal of Physics. March 2013, 15 (3): 033018 [2014-01-15]. doi:10.1088/1367-2630/15/3/033018. (原始内容存档于2021-05-07).
- 赵建林. . 北京: 高等教育出版社. 2006. ISBN 7-04-019268-3 (中文(简体)).
- Halliday, David; Resnick, Robert; Walker, Jearl. . USA: John Wiley & Sons, Inc。. 2005: pp. 1002–1004.
- Laloe, Franck, , Cambridge University Press, 2012, ISBN 978-1-107-02501-1
- John R. Violette. . Hampton Roads Publishing. 12 May 2005. ISBN 978-1-61283-273-9.
- Griffiths, David J., , Prentice Hall, 2004, ISBN 0-13-111892-7
- Sakukrai, J. J.; Napolitano, Jim, 2nd, Addison-Wesley, 2010, ISBN 978-0805382914
- Richard Phillips Feynman. . Penguin. 1990. ISBN 978-0-14-012505-4.
