量子力學入門

19世纪末，人们普遍认为，经典物理的宏伟框架似乎已经接近完成了，但对于一些新的实验发现，经典物理不能作出合理解释，因此，这种观念受到了挑战。在宏观尺度低速运动状态下，经典物理学理论有着完美的应用，但在解释大量微观粒子运动或物体以极高的速度运动时，经典理论遭受了巨大的困难。一种关于全局的观点认为，总的来说，从普通的观测中得到的结果受到了观测和理论预言的挑战（经典物理已经给不出可能的解释）。逐渐显露的景象是，宇宙表现出的行为倔强地违背着我们的常识。

在大尺度层面，相对论告诉我们对不同的观测者来说时间流逝的快慢并不相等。物质能转变为能量，反之亦然。两个以超过0.5倍光速的速度相向而行的物体无法以超过光的相对速度接近对方，时间历程会在接近大质量物体时变慢等等。事物并不是以我们的经验所习惯的方式运作着的。

在小尺度层面，奇异的现象更是无处不在。我们无法描述一个光子或电子从出发点到它被发现点之间的确定的位置或是运动轨迹。我们无法用日常的经验来判断一个粒子将在何处出现。它甚至会有一定的概率在一个封闭边界外出现。概率成为这个尺度上一切相互作用的关键因素。讨论任何原子尺度上的粒子的运动轨迹是没有意义的，因为如果我们要精确的测量粒子的位置，对其速度的测量的准确度就会降低，反之亦然。

在经典物理的时代，牛顿和他的追随者们相信光的本质是粒子，而另外一部分人（惠更斯等人）则认为光是在某种介质中传播的波。物理学家们并没有去寻找实验去证明某一方观点是否正确，而是设计了能够显示出光的频率等属于“波动性”的特征的实验，同时也有能显示出动量等“粒子性”特征的实验。而在此后的一些实验观测中，尺度较大的粒子，比如原子甚至是一些分子都显示出了“波动性”的特征。

1927年，尼尔斯·波尔这样写到：“如果有人没有被量子论所震惊的话，他就没有理解它。”

由左至右分別為︰普朗克、愛因斯坦、玻爾、德布羅意、玻恩、狄拉克、海森堡、泡利、薛定諤、費曼。

量子力学的基本问题源自17世纪对光的本质的研究以及19世纪初电和磁的本质被揭示出来。

1690年，惠更斯提出了光波动说用以解释干涉和折射现象，[9]而艾萨克·牛顿坚信光微粒说，即光是由极其微小的粒子构成的，他把这种粒子叫作“光微粒”。

由于牛顿本人的高度权威，光微粒说在很长的一段时间占据着上风，1827年，托马斯·杨和奥古斯丁·菲涅耳用实验证明了光存在干涉现象，这是和“光微粒说”不相容的。随着光波动说的数学理论逐渐完善，到19世纪末，无论是实验还是理论上，牛顿的理论都失去了以往的地位。

不久之后的一些实验现象如光电效应，只能把光看作“一份一份”的或是将其量子化才能得到合理的解释。当光照射在金属表面，电子会离开初始位置逸出。这种现象的一些特点只能在光的能量不连续的假设下才能被合理解释。在一个光电设备（照相机的曝光表等）中，光照射在金属感应器表面使得电子逸出。增加光的强度（同一频率的光）能够让更多的电子逸出。而如果想要使电子的速度更快也就是动能更大，必须增加光的频率。因此，光强只决定了光电流的大小，也可以说是电路中电压的大小。这个现象和传统的波动模型相悖，因为传统模型是源自对声波和海洋波的研究，这个模型的结论是，振动源的初相位也就是强度大小决定了所产生波的能量大小。同时，如何让表现出光的粒子性和波动性的实验现象和谐共处的问题，也摆在了物理学家的面前。

1874年，乔治·强斯顿·史东尼首次提出了电荷的概念，它是带电体的基本量，不能再被拆分成更小的部分。电荷也就成为了第一个被量子化的物理量。

1873年，詹姆斯·克拉克·麦克斯韦给出了著名的麦克斯韦方程，在理论上证明振荡的电路能够产生电磁波，这使得纯粹的通过电磁测量手段来测量电磁波的速度成为了可能。而测量结果显示电磁波的速度非常的接近于光速。也就是说，光也是一种电磁波。[10]亨里克·赫兹制作了一个能够产生低于可见光频率的电磁波（现在我们称之为微波）的仪器。[11]早期研究的争议在于如何解释电磁辐射的本质，一些人认为这是因为其的粒子性，而另一些人宣称这是一种波动现象。在经典物理里，这两种思想是完全相悖的。

把光看做一种亚原子粒子无法解释这样的干涉现象--气泡上的彩色条纹（薄膜干涉）。除非我们把光看成一种波。这张图片展示了类似于水波的正弦波在厚度不均匀的胶片的两个表面反射而产生干涉现象的情景。这只是对光波的粗略的近似描述，以便于理解。

量子力学正式开始于马克斯·普朗克里程碑式的于1900年发表的关于黑体辐射的论文，[12]在这篇论文里，第一次出现了量子假设。普朗克的工作让人们认识到，无论是光波动说还是光微粒说都不能单独地合理地说明电磁辐射现象。

1905年，爱因斯坦扩展了普朗克的量子假设，并用其成功的解释了光电效应现象。[13] 波尔给出了他的原子模型，这个模型充分的吸收了普朗克的量子假设。[14]这些工作和20世纪初的其他一些工作创立了“旧量子论”。

1924年，路易·德布罗意提出了物质波假设。此假设的提出成为了一个转折点，从那以后，一个更高级且更完整的量子力学逐渐出现了。[15]在20年代中期对“新量子力学”或“新物理学”做出了重要贡献的物理学家还有，马克斯·波恩，[16] 保罗·狄拉克，[17] 维尔纳·海森堡，[18] 沃尔夫冈·泡利，[19]以及埃尔温·薛定谔。[20]

20世纪40代末到50年代初，朱利安·施温格、朝永振一郎、理查德·费曼和弗里曼·戴森合作或分别同时发展了量子电动力学，它研究的对象是电磁相互作用的量子性质（即光子的发射和吸收）、带电粒子的产生和湮没、带电粒子间的散射、带电粒子与光子间的散射等等。此后，默里·盖尔曼发展了描述夸克胶子之间强相互作用的量子色动力学。

当一束白光通过光学棱镜、光栅、锥面镜或者是雨后的彩虹时，它就被分解成了各种颜色的光。这样的光谱说明了，白光是由所有频率的有色光组成的。

在受热或者是受某种能量激发时，由单一元素组成的样品能够辐射出可见光，它的光谱被称为放射光谱。光谱和元素的种类以及外界加热的温度有关。和白光的光谱不同，这种光谱是间断的，并不是从紫色到红色连续出现每种颜色，而是分别形成了一些具有不同颜色的窄带（亮线），窄带与窄带之间存在黑色暗带，这就是所谓的“线状光谱”。放射光谱的谱线能够超出可见光的范围，我们能使用特殊的照相设备和电子设备检测到它们。

氢原子光谱中的亮线，图片来自NASA

氮原子光谱中的亮线

最初，人们认为原子电磁辐射的模式是类似于小提琴的一根弦“辐射”出声波那样的——不仅仅只有一种基本频率（整个弦一起在最低频率振动，同时向一个方向运动），还应该有高频谐波（频率是基频的整数倍，弦上不同的地方位移可能相反，类似于正弦波）的成分。但如何用数学语言简洁合理的描述某种元素的谱线分布一直困扰着人们，直到1885年，才由约翰·巴耳末给出了一个简单的公式来描述氢原子的谱线，如下：

${\displaystyle {\frac {1}{\lambda }}=R\left({\frac {1}{2^{2}}}-{\frac {1}{n^{2}}}\right)}$

${\displaystyle \lambda }$表示波长, R是里德伯常量，而n是大于2的整数。（此处分母2^2不可更为4）
这个公式还能推广到适用于别的一些元素的原子光谱。

进一步的发展便是彼得·塞曼发现了塞曼效应，随后亨得里克·洛仑兹给出了其物理解释（两人一起获得了1902年诺贝尔物理学奖）。洛伦兹假设氢原子的谱线是由电子跃迁产生的，这很容易由对原子本身的分析得到。由于运动的电子会产生电磁场，因此电子的行为就能够被外磁场所影响，就像磁铁之间互相吸引一样。

若假设电子在特定的不同的轨道上跃迁时向外辐射电磁波而形成谱线，赛曼效应就得到了合理的解释。但经典物理做不到这些，它不能告诉我们电子为何不螺线状坠入原子核，不能告诉我们为何原子的轨道有辐射谱线需要的性质来描述巴尔末公式，不能告诉我们为什么电子的光谱都不是连续的。而这一切，都预示着，变革即将到来。

经典物理有一个关于黑体辐射问题的推论：当频率增大时，黑体辐射将会释放出无限大的能量（瑞利-金斯定律）。这个结论当然是荒谬的，可观测到的实验现象也是让人无法理解：黑体的辐射光谱的能量密度随着频率从零开始递增达到一个峰值（峰值频率和辐射源的温度有关）后再逐渐衰减至零。1900年，马克斯·普朗克给出了一个能够解释黑体光谱实验现象的经验公式（利用数学插值法），但他不能使之和经典物理相协调。他得出的结论是，和从前大家所普遍相信的不一样，经典物理并不适用于微观世界。

普朗克的公式适用于任意的波长和频率的情况下，同时限制了发散的能量传输。“在经典物理里，...振动的能量仅仅取决于其振幅，而振幅的大小是没有任何限制的。”[21]他的理论导出了一个重要推论，辐射的能量和辐射的频率成正比关系，频率越高，能量越大。为了解释这个推论，他做了这样的假设：宏观的辐射源（如黑体）是由数量巨大的基本谐振子构成的，振子的频率在零到无穷大之间分布（不久以后证实了这种基本谐振子就是原子或分子），于是普朗克做了更进一步的假设：任一振子的能量“E”和它的频率“f”成正比，而且是某种整倍数关系。如下所示：

${\displaystyle E=nhf,\,\!}$

在此式里，n =1, 2, 3,..。“h”由普朗克首先引入的是基本物理学常数，为了纪念他的功绩，被命名为“普朗克常数”。[22] h是一个非常小的量，大约是6.6260693×10^-34焦耳·秒。

如果我们知道“h”和光子的频率，就能用这个方程计算出光子的能量。给出一个例子：如果一束光的频率是540×10¹²赫兹。那么这束光的每一个光子的能量就是“h”×(540×10¹² hertz)。因此光子的能量就是3.58×10^-19焦，就是大约2.23电子伏特。

如果用这种方式来描述波所具有的能量，波所携带的能量就成了一份一份的。普朗克将这种“份”命名为“量子”，就这样，电磁波被重塑成了类似于粒子的物质。电磁波的能量被量子化后，量子力学诞生了。能量的大小和电磁波的频率息息相关。对于可见光来说，能量和颜色相关，因为颜色是由其频率决定的。但读者应该认识到，我们虽然用了诸如“份”，“波”，“粒子”等来自于宏观世界的概念来描述量子世界，但实际情况比这复杂的多，我们这样做是为了方便读者理解。

在早期关于光的研究中，存在对光的两种相互竞争的描述方式：作为波在真空中传播，或是作为微小粒子沿直线传播。普朗克表述了光的能量是量子化的，凸显出了它的粒子性。这种表述让我们明白了光是如何以量子化形式传播能量的。但是，光的波动性又是我们理解衍射和干涉之类的现象所必须的。

1905年，爱因斯坦引入普朗克常量来解释光电效应而获得成功，他假设一束光是由大量的光量子（也就是后来的光子）组成的，[23]在这个前提下，一个光子具有的能量是不变的且和其频率成正比关系（不同的光子具有不同的能量）。尽管这个建立在普朗克量子化假设上的理论听起来类似于牛顿的光微粒说，但爱因斯坦的光子同时还具有频率这种性质，其能量还和频率成正比，这是和过去不一样的，但无论如何，光微粒说以一种折衷的方式回来了。[24]

粒子和波的概念都源自于我们日常生活中的经验。我们不看“看见”单独的光子（事实上我们的观测就是利用光子来进行的），我们只能间接的观察它们的一些性质。比如我们从表面覆盖着油膜的水坑里看见光反射出各种颜色。把光看做某种波，我们能解释这种现象。[25]而对于其它一些现象，比如照相机中的曝光表的工作原理，我们又习惯把光看做某种和感光屏相撞的粒子。无论是哪种方式，我们都是在用日常生活中由经验得到的一些概念来描述那一个我们永远无法直接看到或者感知到的世界。

当然，无论是波动说或者微粒说都不能让人完全满意。总的来说，任何一种模型都只是对实际情形的近似描述。每一种模型都有它适用的范围，超出这个范围后，该模型也许就不能作出精确的描述了。牛顿力学对于我们的宏观世界来说仍是足够实用的。我们应该认识到波和粒子的概念都是源自于我们的宏观世界的，我们用它们来解释微观世界在一定程度上并不合理。有些物理学家，比如班尼旭·霍夫曼使用了“波粒二象性”来描述这种微观世界的“实在”，而在接下来的讨论中，使用“波”还是“粒子”将取决于我们从哪个方向去研究量子力学的现象。

普朗克常数最初只是连接光的能量和频率的比例因子。波尔在他的理论中推广了这个概念。波尔用原子的行星模型来描述电子的运动，但起初他并不理解为何2π和普朗克常数一起出现在了他推导出的数学表述中。

不久之后，德布罗意假设电子也如同光子那样具有频率，而其此频率必须满足电子在特定轨道稳定存在的驻波条件。这就是说，电子波圆周运动的轨迹必须光滑的衔接起来，波峰和波谷连续分布。中间不能有间断，周长的每一段都是振动的一部分，而且波形不能重叠。很自然的我们可以得出轨道的周长“C”是波长“λ”的正整数倍。我们在知道轨道半径“r”之后就能够计算出周长，再利用周长计算出电子的波长，数学表述如下：

${\displaystyle C=2\pi r=n\lambda \,\!}$

解出λ得：

${\displaystyle \lambda =2\pi r/n\,\!}$

这个方程用半径“r”表示出了决定频率和波长的轨道周长，就这样，因为半径和周长之间的固有关系，2π再一次出现在了量子力学中。[26]

1925年，当维尔纳·海森堡在完成他的完整量子理论表述过程中（原文可能有问题，写的是波函数，怀疑写错了人），傅里叶级数是计算中经常出现的数学形式，而在傅里叶级数中2π这个因子可以说是无处不在。引入约化普朗克常数（h/2π）后，可以约去表达式中大多数的2π，从而使方程更加简洁。数年之后，约化普朗克常数出现在了狄拉克方程中，它也因此得名“狄拉克常数”。现在，虽然我们已经谈了这么多关于这个常数的发展和历史，却还没有涉及到更深层的意义——为什么在理论运用中它比普朗克常数更简便或是更普适？

如上所述，任何电磁波的能量等于它们的频率乘以普朗克常数，而光速等於頻率乘以波長。波是由波峰和波谷组成的。经过一个完整的周期，波上的各点会回到振动的初始位置。例如，某一点开始的时候是波峰，经过一个周期后它将再次回到波峰。一个周期恰好和一个圆周相对应，都是360度，也就是2π弧度。1度是指弧长是圆周长的1/360的圆弧所对应的角度的大小。随着圆的转动，圆周上的一点会画出正弦曲线的轨迹。（观看相关演示动画，请访问 （页面存档备份，存于））

现在取一段圆弧，使其长度等于其半径。用直线把圆心和圆弧的两端分别连起来。这两条半径的夹角就是1弧度。圆周和波的周期都是2π弧度。既然一个周期等于2π弧度，“h”除以2π后，这两个2π就相互抵消了，只留下一个以弧度为单位的变量。因此如果把h/2π表示成一个常数，乘以波的频率（周期除以2π）时，一弧度就对应着一焦耳的能量。约化普朗克常数，读作“h一横”（h-bar），表示为：

${\displaystyle \hbar ={\frac {h}{2\pi }}\ }$.

约化普朗克函数使计算电磁波的能量时使用的单位由周期变成了弧度。h和ħ的作用只是将频率的单位（量纲）转换成能量的单位（量纲）。

之所以在量子力学的数学表述中更多出现的是约化普朗克常数，主要有以下原因：角动量和角频率都是以弧度为单位的，使用ħ可以免去角度和弧度之间的相互转换。在量子力学的方程中使用ħ可以化简很多分式。而在其他一些情况下，比如波尔的原子模型中，表述轨道角动量时自然而然的就出现了ħ（h/2π）。

h的数值取决于波长以及能量的单位的选取。如果能量使用电子伏特（eV，粒子物理学的常用单位）而波长使用埃（ångström，10^-10m）作为单位，那么一个光子的能量大约是_eV = 12400/λ_ångström。这种表示方式容易记忆且避免了使用国际单位制中的小值。[27]

玻尔的原子模型，氢原子的电子正在跃迁至n=1的基态

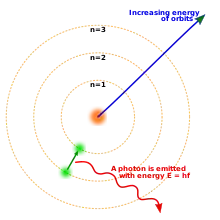
1887年，J·J·汤姆生领导的一个研究小组发现了一种带着一个单位负电荷且质量极小的基本粒子并把它命名为电子。通过金箔实验，物理学家认识到物质的内部几乎是真空的，原子核只占了原子很小的一部分。[28]这个事实清楚之后，就可以很自然的假设负电子在轨道上环绕着原子核运动，就像太阳系的行星那样。但这种简单的类比的后果就是：根据经典电动力学，电子在运动时会不断向外辐射电磁波，失去能量的电子最终将会坠入原子核中。以此推论，电子大约只能存在百分之一微秒[29]。因此，20世纪初困扰物理学家们最大的问题就是：电子是如何保持稳定轨道的？

1913年，为了解决这个问题，尼尔斯·玻尔假设了电子的轨道是量子化的（不连续）。这就是著名的玻尔原子模型。玻尔的基本假设是：电子只能占据原子核外的特定轨道[30]这些轨道能够在对单一元素的原子的光谱分析后得出,並且移動中的電子並不向外放出電磁輻射。

玻尔指出了光微粒说和光波动说都不能独立的说明经实验观测到得光的特性。所有形式的电磁辐射都在一些实验中表现出波动性，却又在别的一些实验中表现出粒子性。以此为根据，玻尔阐明了对应原理，此原理针对一些相对应的概念，如波动性和粒子性，位置和动量等。

1924年，德布罗意从玻尔的发现中发展出了波粒二象性理论用以描述亚原子粒子同时具有的波和粒子性质的特性，并给出了数学表述。德布罗意推广了玻尔模型，一个绕着原子核旋转的电子能够被看作具有一些类似于波的性质。特别的是，只有环绕原子核形成驻波时，电子才能被观测到。“驻波”的波形无法前进，因此无法传播能量。它的一个典型例子是两端固定的一根弦，拨动两端固定张紧的弦使其振动，一开始需使弦的两端的振幅为零，使波经两固定端反射可干涉产生驻波。同时，弦的两固定端必为节点（也就是振幅为零的点）。当弦上产生驻波时，弦长L为半波长的正整数倍。而回到原子模型上，如果要使波动运动轨迹光滑衔接形成一个简单闭合曲线，波必须由波峰和波谷连续构成。而电子的轨道是圆周轨道，每一个电子就必须以它自己的驻波形式来占据特定轨道。

1932年诺贝尔物理学奖获得者，维尔纳·海森堡在1925年建立起了完整的量子力学理论。

1925年，基于德布罗意的物质波模型，埃尔温·薛定谔假设电子就是那样环绕原子核的波，然后对电子的行为进行了数学分析。他并没有把电子比作绕行星转动的卫星，而是直接把它们看作在原子核周圍的某种波，并且指出描述各個电子的波函数都是互不相同的。而这种波函数所遵守的方程式被命名为薛定谔方程，以纪念他为量子力学做出的贡献。薛定谔方程分别从三个性质出发描述了波函数（后来沃尔夫冈·泡利又加入了第四个性质：自旋）：

1. 轨道的名称表明了粒子波的能量高低（离原子核越近能量越低）。
2. 轨道的形状，球形或者其他。
3. 轨道的倾角，决定了电子对z轴的磁矩。

这三种特性被归纳成描述电子量子态的波函数。量子态代表着电子的这些特性，它适时的描述了电子的状态。电子的量子态由它的波函数给出数学描述，我们用希腊字母${\displaystyle \psi }$来表示波函数(${\displaystyle \psi }$，读作"[sai]").

这三个被波函数描述的特性分别被称之为电子的量子数。第一个描述轨道能量的量子数叫作主量子数，这个量子数对应着波尔原子模型里决定原子能级的n。n是正整數，由1開始。一個電子的主量子數是n代表他是第n電子層的電子；也有代號，即K對應n=1的情況、L對應n=2如此依字母順序。

第二个量子数，角量子数，用l（小写L）来表示。它描述了轨道的形状，轨道的角动量决定了轨道的形状。角动量的变化率等于系统所受合外力的力矩。换句话说，角动量反映了旋转物体在外力作用下其速度改变的难易程度。角量子数"l"代表着电子对原子核的角动量。l在原子中的電子軌域允許值自0開始直到n-1。其對應的是軌域種類，l=0~3使用的符號分別是s、p、d、f，[註 1][31]，l值為4以上時則依字母順序表示為g、h等等。

薛定谔方程的第三个量子数描述了电子的磁矩，此量子数用m或带下标l的m来表示，这是因为磁矩跟第二个量子数l有关。

1926年5月，薛定谔证明了海森堡的矩阵力学和他的波动力学对电子性质和行为的预测结果是相同的；而它们在数学上也是等价的。但他们仍然在对各自理论的物理诠释上无法取得一致的意见。海森堡认为间断的量子跃迁的存在是很自然的，但薛定谔仍寄希望于得到一个连续性的，传统的，如同波动说那样的理论来让（用威廉·維因的话来说[32])"海森堡的愚蠢的量子跃迁"从物理学里彻底消失。[註 2]

1927年，海森堡利用他的矩阵力学和一些理想实验推导出了一个微观尺度下物质和能量的重要结论。他发现在测量粒子动量和位置的时候会导致h/4π的误差（两者误差相乘）。测量时位置的误差越小，动量的误差就会变得相当大。而h/4π就是这个误差的下限（也就是说两者误差的乘积大于等于h/4π）。这一结论最终被称作不确定性原理。

量子力学严格限制了测量处于运动状态的亚原子粒子时的精确度。观测者可以精确测量粒子的位置或是动量，但无法同时精确测量两者。这个限制意味着对其中一种属性的测量达到极高的精确度时，对另一种属性的测量的误差将会趋于无穷大。

海森堡在早期一个关于不确定原理的演讲里这样提到了玻尔模型：

“你大可以认为，电子的轨道并不是真正的轨道。实际上，在每一时刻电子总有一个属性是我们无法确定的，要嘛是动量，要嘛是它的位置，这是不确定关系得出的结论。只有接受了这种理念，我们才可能描述电子的轨道是什么，而它的确是这样的。”[33]

不确定性原理给出的一个重要结论就是在某一时刻，我们不能确定电子在轨道上的确切位置，我们只能给出电子在某一位置出现的可能性。计算出电子可能出现的位置，给出可能出现的相关轨道，我们就可以给出一种和传统图景不同的原子描述——电子在原子核周围形成了电子云，它分布在原子核周围，在靠近原子核的一些区域，电子云拥有最大的密集度，这代表电子在这些区域出现的概率最大，在远离原子核的区域，电子云变得稀疏了，电子在这些区域出现的概率较小。数学上我们把这种点状云称为概率分布，这是它的一种较形象的表述方式。波尔的原子模型中每个轨道对应的量子数n就成为了n维球面，被描绘成环绕原子核的概率电子云。

如果一个电子的位置无法被测量出，我们就不能描述它处于哪一个特殊的位置了。我们能做的就是计算出电子在轨道上某些位置出现的机率。换句话说，量子力学只能给出发生某种可能的结果的机率。海森堡从不确定原理出发，继续思考观测电子的问题，得出的结论居然是微观粒子只在我们观察它的时候才存在！注意他针对的是粒子本身，而不是它们的轨道。尽管他所阐述的理论看上去是荒诞且强烈的违背着我们的直觉的，量子力学仍然只能从概率分布出发来计算给定轨道下电子的位置。

尽管海森堡的矩阵力学允许电子出现在无限多的位置，这并不意味着电子可以出现在空间中的每一个地方。有一些条件限制了电子，使其必须占据某些特定的概率分布描述的位置。波尔模型是通过电子的能级来描述电子行为的，矩阵力学和它是相容的。因此，一个电子所出现的n维球面对应着离原子核某一特定距离，而正是这个距离决定了电子的能量。正是这个条件制约了电子的位置。电子可能存在的位置的数目又被称为相空间中的相格数[34]根据不确定原理，经典相空间不能被无限细分，因此在一个轨道上电子能占据的位置数就是有限的了。电子在原子里的位置取决于它的轨道，而一个轨道终止于原子核，并且离下一个轨道开始的位置很近。

自牛顿以来的经典物理学告诉我们，如果我们知道某一时刻行星和恒星的位置和运动状态，我们就能够预测它们在未来任何时刻运动状态。不确定原理则告诉我们这对于亚原子世界是不适用的。我们不能同时精确测量出微观粒子位置和动量，对于粒子未来的运动状态，我们只能给出一种概率分布，该分布只能告诉我们在未来它处在这种状态的可能性。

源自波粒二象性的不确定性原理的影响只在亚原子尺度时显现出来。尽管这些现象违背了我们的直觉，以不确定原理著称的量子力学仍然不断引领着科学技术的进步，如果没有它，我们也就不会拥有电子计算机，荧光灯以及医学影像设备。

对于单个电子而言，薛定谔的波动方程及其独特的波函数和海森堡的量子化的点粒子的概率分布一样在空间中散开，因为波本身就是分布很广的扰动而不是点粒子。因此，薛定谔的波动方程能够得到和不确定性原理相同的结果，因为位置的不确定性在波的扰动的定义中就表现出来了。只有海森堡的矩阵力学才需要定义不确定性，因为它是从粒子的观点出发的。薛定谔的波函数显示电子总是处于概率云中，在它像波一样展开的概率分布中。

马克斯·玻恩在1928年发现，薛定谔的波函数的平方（为了得到振幅的平方）是电子位置的概率分布。[35]对于电子的位置可以直接测量而不会得到一个概率分布，是因为电子暂时失去了波的性质。没有了波的性质，薛定谔的关于电子的波的特性的预言也都失效了。对粒子的位置的测量使粒子失去了波的性质，以至于薛定谔的波动方程失效了。电子一经测量再也不能被波函数所描述，它的波长变得很短并且它与测量设备的粒子相互纠缠，这种现象就是所谓的坍缩。

泡利不相容原理表明了一个原子里的每一个费米子（自旋不为整数的粒子）必然具有不相同的量子状态。它的一个非常重要的推论就是对任何原子，两个电子都不能具有同样的量子态。（对于自旋为整数的玻色子，则其不服从泡利不相容原理。）

沃尔夫冈·泡利给出了泡利不相容原理的简单表述：

"一个原子中没有量子数完全相同的两个电子。"[36]

沃尔夫冈·泡利的不相容原理是从他称做“量子自由度的双重值”的理论发展而来的。这个理论是为了解释氢原子光谱中成对出现的两根非常接近的谱线。这个现象意味着原子的磁矩比预先设想的要大。

1925年初，乔治·乌伦贝克和撒姆爾·高斯密特（Samuel Goudsmit）提出电子可能像地球那样绕自身的轴自转的假设，他们把这种特性称之为自旋。自旋能够解释多出来的那部分磁矩，并且让两个电子在不违反不相容原理的条件下占据同一个轨道成为了可能——只需要它们自旋方向相反。这时就需要一个新的量子数来描述原子自旋的动量。[37]

就这样，我们已经确定电子具有四个量子数：

• n：主量子数；
• l：角量子数；
• m_l：磁量子数；
• m_s：自旋量子数。

泡利举了一个例子：

“在氦原子中有两个电子占据1 s轨道，根据不相容原理，这两个电子必须有不同的量子数，而n, l,和m_l这几个量子数是相同的，而且他们的自旋量子数s的值都等于1/2[36]，因此它们的m_s一个是+1/2,而另一个是-1/2。”

1928年，保罗·狄拉克推广了用于描述自旋电子的泡利方程而使之与狭义相对论相容。于是这个理论便能够处理速度接近光速的微观粒子的运动问题，比如在轨道上运动的电子。使用最简单的电磁相互作用理论，狄拉克算出了由电子自旋而产生的磁矩，他发现实验观测到的值和经典物理所想象的那种自旋所得出的值大了很多。他完全的解决了氢原子光谱的问题，并从他的理论中推导出了索末菲关于氢原子光谱精细结构的公式。

狄拉克方程有时会解出电子具有负能阶，于是他提出了一个新颖的假设：在动力学空间中存在着正电子。这最终导致了多粒子量子场论的诞生。1930年，狄拉克编写了关于量子力学的第一本现代意义上的教科书，书中整合了海森堡的矩阵力学，薛定谔的波动力学和他自己的量子变换理论，同时也使之与狭义相对论相适应。《量子力学原理》（The Principles of Quantum Mechanics）是公认的经典著作，直到今天也具有相当的参考价值。

直到现在，所有的量子理论主要都是集中在对氢原子光谱的研究上。根据旧量子论，每一种元素的原子的光谱都是独特的。由于电子和原子核不能被直接观测到，科学家们不可能直接去研究它们的行为。即使在今天，我们使用掃描式穿隧電子顯微鏡，也只能得到模糊不清的原子图像。迄今为止，对量子力学的实验验证还只是在对氦和氢原子的辐射光谱研究上，它的数学表述被用来解释和说明辐射光谱。因此，量子力学有时也被认为是一种数理物理学。

兩個量子的疊加與可能的解。

泡利不相容原理指出在同一系統下的兩個電子不可能處於同一狀態。大自然拋棄了這種可能性，但卻允許兩個電子可以在上面「疊」有兩種狀態。回想波函數，穿過雙狹縫並在一瞬間以疊加的其中一種狀態呈現在顯示屏幕上。沒有什麼是確定的，除非疊加的波「坍縮」，這時候就會有一個電子以符合概率的方式立即顯示在某個地方，這個概率即波形疊加後的振幅的平方。上述情況已十分抽象難解了。關於光子的纏結，在此有一個較為具體的思考方式，有兩個光子在同一事件中疊加了兩個相對立的狀態，如下︰

可以試著在腦海中想像，把疊加的其中一個狀態標記為藍色，再把另一個狀態標記為紅色，在稍後會顯現成紫色的狀態。兩個光子是在同一個原子事件中產生出來的。這兩個光子可能是水晶吸收特定頻率的光子並發射出頻率為原始值之半的兩個光子所激發而成的。因此這兩個光子顯現出「紫色」。如果有位實驗者現在要作測定光子是紅或藍的實驗，這個實驗會把光子從原本具有「紅」、「藍」兩個狀態改變成只有其中一個狀態。這個愛因斯坦曾經如此想像過的問題是，如果其中一個光子不斷在實驗室的鏡子之間持續彈跳，而另一個光子已經移動到最近的星星的一半路程，當成對的其中一個光子顯現出自身是紅或是藍的時候，就意味著那顆遠在千里之遙的光子也必須失去「紫色」的狀態。故每當檢查光子的時候，光子就必定顯現成相對於成對光子的另一個狀態。

假設有某些物種帶有雄性或雌性這兩種性別特徵的遺傳潛力。牠們會隨著環境的變化轉變成雄性或雌性。牠們也許會一直保持著不確定的狀態直到天氣轉變成嚴寒或酷暑。然後牠們會顯現出一種性別特徵，以後天改變的方式、雄激素或雌激素等高階系統鎖定到那個性別狀態。自然界中確實有符合上述情節的情況，不過現在要再想像如果有一對雙胞胎出生，並且有一股自然之力禁止這對雙胞胎顯現出同一性別。之後如果雙胞胎的其中一個到了南極，並轉變成雌性，此時另一個雙胞胎將無視當地氣候直接轉變成雄性。這樣的世界相當難以解釋。在南極洲的一隻動物會影響到牠那遠在紅木市的雙胞胎兄弟這種事要怎麼樣才會發生？美國加州？心電感應？什麼？要怎麼樣才能瞬間作出變化？即使是來自南極洲的無線電訊息都要花費一段時間。

為了證明量子力學是個不完備的理論，愛因斯坦從理論的預言開始著手，該理論預言，那些過去已經相互作用的兩個或更多粒子，在之後的測量中，可以顯示出很強的聯繫。他试图用经典的方法来解释这个看似的相互作用，即通过他们平常的过去，而不是幽灵般的超距作用。这个争论最终在一篇著名的论文中得到了解决，爱因斯坦，波多尔斯基和罗森（1935，Einstein-Podolsky-Rosen，简写为EPR）在这篇文章中提出了现在所谓的EPR悖论。在假设定域实在性的基础上，EPR试图从量子论的角度出发，解释一个粒子同时具有位置和动量两种属性，而对应的哥本哈根解释则认为只有其中之一实际存在且仅仅在被测量的时刻存在。EPR总结说量子论是不完整的，因为它没有考虑到自然世界中明显存在的物理属性（爱因斯坦，波多尔斯基和罗森，1935，已经是在物理杂志上被引用最多的爱因斯坦的文章）。同一年，埃尔温·薛定谔使用“缠结”这个词并且声称：“相对于把它称为量子动力学的特征之一，我更想称它为量子动力学的专有特征”。[38]纠缠是否是一个真实的条件这个问题一直到现在仍然存在争议。[39]贝尔不等式是对爱因斯坦声明最有力的挑战。