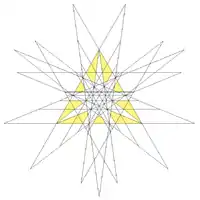
大二十面體
在幾何學中,大二十面體是一種星形二十面體,由20個正三角形組成,其在非凸均勻多面體被編號為U53、在溫尼爾多面體模型被編號為W41,是四種星形正多面體之一,對偶多面體為大星形十二面體。
 (按這裡觀看旋轉模型) | ||||
| 類別 | 星形正多面體 星形二十面體 | |||
|---|---|---|---|---|
| 對偶多面體 | 大星形十二面體 | |||
| 識別 | ||||
| 名稱 | 大二十面體 | |||
| 參考索引 | U53, C69, W41 | |||
| 鮑爾斯縮寫 | gike | |||
| 數學表示法 | ||||
| 考克斯特符號 | ||||
| 施萊夫利符號 | {3,5/2} | |||
| 威佐夫符號 | 5/2 | 2 3 | |||
| 性質 | ||||
| 面 | 20 | |||
| 邊 | 30 | |||
| 頂點 | 12 | |||
| 歐拉特徵數 | F=20, E=30, V=12 (χ=2) | |||
| 虧格 | 0 | |||
| 組成與佈局 | ||||
| 面的種類 | 20個正三角形 | |||
| 面的佈局 | 20{3} | |||
| 頂點圖 | (35)/2 | |||
| 對稱性 | ||||
| 對稱群 | Ih, H3, [5,3], (*532) | |||
| 特性 | ||||
| 正、等面、等邊、等角 | ||||
| 圖像 | ||||
| ||||
性質
大二十面體共有20個面、30條邊和12個頂點[1][2],20個面中,全部都是正三角形,且每個頂點都是5個三角形的公共頂點,但其以類似五角星的方式安排面的位置,使面互相相交,頂點圖為五角星,在施萊夫利符號中可以用{3,5/2}來表示,而在考克斯特符號中以![]()
![]()
![]()
![]()
![]()
![]()
![]() 表示。
表示。
參考文獻
- Wenninger, Magnus. . Cambridge University Press. 1974. ISBN 0-521-09859-9.
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. 3rd. Tarquin. 1999. ISBN 978-1-899618-32-3. MR 0676126. (1st Edn University of Toronto (1938))
- H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 6.2 Stellating the Platonic solids, pp.96-104
- . mathconsult.ch. [2016-09-02]. (原始内容存档于2016-03-25).
- . bulatov.org. [2016-09-02]. (原始内容存档于2016-03-27).
- . dmccooey.com. [2016-09-02]. (原始内容存档于2016-09-02).
- . dmccooey.com. [2016-09-02]. (原始内容存档于2016-03-24).
- . bulatov.org. [2016-09-02]. (原始内容存档于2015-09-06).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.