截角大星形十二面體

在幾何學中，截角大星形十二面體又稱小複雜截半二十面體（small complex icosidodecahedron）是一種退化的星形均勻多面體，由於其可以視為截角的大星形十二面體或過截角的大二十面體，其截角產生的稜兩兩互相重合，外觀與正二十面體無異，但其有12個五邊形面隱沒在立體內部，通常需要藉由讓三角形面變透明才能看出整個立體的構造[2]。

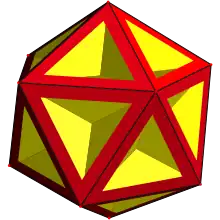
將外層三角形面（紅色）中間打洞的截角大星形十二面體，可以看到內側互相相交的五邊形面（黃色）。
截角大星形十二面體
截角大星形十二面體
類別退化均勻星形多面體
識別
鮑爾斯縮寫
cid在维基数据编辑
數學表示法
考克斯特符號
node 3 node_1 5 rat d2 node_1 
施萊夫利符號t1,2{3,5/2}
威佐夫符號
5 | 3/2 5[1]
性質
面32
邊60
頂點12
歐拉特徵數F=32, E=60, V=12 （χ=-16）
組成與佈局
面的種類12個五邊形{5}
20個正三角形
面的佈局
12{5}+20{3}
頂點圖(3/2.5)5
(3.5)5/3
對稱性
對稱群Ih, [5,3], *532
圖像

(3/2.5)5
(3.5)5/3
（頂點圖）

性質

小複雜截半二十面體由12個五邊形和20個正三角形組成，其共有32個面、60條邊和12個頂點，若不計重合的邊，則會導致立體中的每條稜都是四個面的公共稜[3]。這種立體是均勻多面體的一種退化形式，在考克斯特的書中，這種形式被以威佐夫記號5 | 3/2 5。[1]

作為複合多面體

小複雜截半二十面體可以視為正二十面體和大十二面體的複合多面體，由於正二十面體和大十二面體其頂點和邊可以互相共用 [4]，其組成成的複合體也稱為小複雜截半二十面體[5][6]

複合多面體
正二十面體 大十二面體 複合體

作為截角多面體

均勻截角即為一般用於產生半正多面體（如阿基米德立體）所用的截角變換[7][註 1]，其結果在考克斯特記號中可以用node 3 node_1 5 rat d2 node_1 表示[11] ，而套用了這種截角變換後會使得大星形十二面體轉變成外觀與一般正二十面體相同的立體，因此在繪製大星形十二面體十通長要是表面的正三角形透明化才能觀察立體的整體。[2]

相關多面體
名稱 大星形十二面體 截角大星形十二面體 大截半二十面体 截角大二十面體 大二十面體
考式 node 3 node 5 rat d2 node_1  node 3 node_1 5 rat d2 node_1  node 3 node_1 5 rat d2 node  node_1 3 node_1 5 rat d2 node  node_1 3 node 5 rat d2 node 
圖像

與小複雜截半二十面體可以視為截角的大星形十二面體，與之類似的退化星形均勻多面體為另一個由星形正多面體截角的結果，其為截角小星形十二面體。[12]

星形正多面體大十二面體小星形十二面體大二十面體大星形十二面體
圖像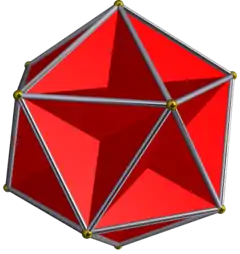
截角圖像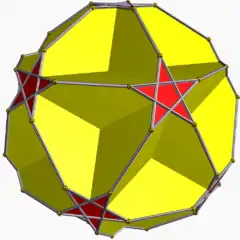
截角名稱 截角大十二面體截角小星形十二面體截角大二十面體截角大星形十二面體

小複雜截半二十面體由12個五邊形和20個正三角形組成，另一種也是由12個五邊形和20個正三角形組成立體為截半二十面体。[13]

參見

註釋
  1. 產生半正多面體所用的截角，即確保截角完後的面皆要等邊的截角。[9][10]

參考文獻
  1. Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P., , Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1954, 246: 401–450, ISSN 0080-4614, JSTOR 91532, MR 0062446, doi:10.1098/rsta.1954.0003 (Table 6, degenerate cases)
  2. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
  3. . math uni-bielefeld. [2019-09-22]. （原始内容存档于2019-09-22）.
  4. . mpifr-bonn.mpg.de. [2019-09-22]. （原始内容存档于2020-12-04）.
  5. Norman Johnson. Guy Inchbald , 编. (PDF). steelpillow. [2019-09-22]. （原始内容存档 (PDF)于2012-03-14）.
  6. Klitzing, Richard. . bendwavy.org. [2019-09-22]. （原始内容存档于2021-01-16）.
  7. Olshevsky, George, Truncation at Glossary for Hyperspace.
  8. Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
  9. Coxeter, H.S.M. Chapter 8: Truncation, Regular Polytopes,[8] pp. 145–154
  10. Norman Johnson, Uniform Polytopes, Manuscript (1991)
  11. Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
  12. Maeder, Roman E. . The Mathematica Journal (Citeseer). 1993, 3 (4): 48––57 [2019-09-22]. （原始内容存档于2021-08-23）.
  13. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.