强连通分量

在有向图的数学理论中，如果一个图的每一个顶点都可从该图其他任意一点到达，则称该图是强连通的。在任意有向图中能够实现强连通的部分我们称其为强连通分量。判断一个图是否为强连通以及找到一个图强连通分量只需要线性时间（Θ(V + E)）。

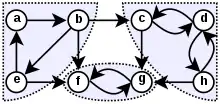
标记了强连通分量的图形

定义

如果有向图的每一对顶点之间在每个方向上都有一条路径，则称该有向图为强连通图。也就是说，顶点对中的第一个顶点到第二个顶点存在一条路径，从第二个顶点到第一个顶点存在另一条路径。在本身可能不是强连通的有向图 $G$ 中，如果一对顶点 $u$ 和 $v$ 之间在每个方向上都有一条路径，则称它们是强连通的。

强连通的二元关系是一个等价关系，其等价类的导出子图称为强连通分量。同样地，有向图 $G$ 的强连通分量是一个强连通的子图，并且在这个子图上是最大的，这意味着在不破坏 $G$ 的强连通特性的情况下，任何来自 $G$ 的额外边或顶点都不能包含在子图中。强连通分量的集合构成了 $G$ 的顶点集的一个子集。

黄色有向无环图是通过将蓝色有向图的每个强连通分量压缩成一个单一的黄色顶点而形成的

如果将每个强连通分量收缩为单个顶点，则得到的图是一个有向无环图。当且仅当有向图不包含具有多个顶点的强连通子图时，它就是无环的，这是因为如果有向图是强连通的，则每个非单调强连通分量至少包含一个有向环。

算法

基于DFS的线性时间算法

几种基于深度优先搜索并能在线性时间内计算强连通分量的算法。

Kosaraju算法使用了两次深度优先搜索。在原始图中，第一次搜索用于决定第二个深度优先搜索的外层循环的顺序，该循环测试已经访问过的顶点，如果没有，则用递归的手段搜索它们。第二次深度优先搜索是在原始图的转置图上进行，每个递归搜索都能找到一个新的强连通分量。[1]这种算法以其首次提出者S·拉奥·科萨拉朱的名字命名，但是并没有被发表，直到1981年才被米查·沙里尔发表。[2]
Tarjan演算法:由羅伯特·塔揚于1972年发表[3]，是一种深度优先搜索方式。

应用

寻找强连通分量的算法可以用来解决2-SAT问题（由带有对于变量对的值的限制的布尔变量构成的系统）：如Aspvall，Plass & Tarjan (1979)所示，一个2-SAT实例是无解的，当且仅当有一个变量v使得v和它的互补被包含在实例的隐含图的同一个强连通分量中。[4]

强连通分量也被用来计算Dulmage–Mendelsohn 分解，一种二分图的边的分类，根据它们能否作为图中的完美匹配。[5]

参考文献

Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 22.5, pp. 552–557.
Sharir, Micha, , Computers & Mathematics with Applications, 1981, 7: 67–72, doi:10.1016/0898-1221(81)90008-0 
Tarjan, R. E., , SIAM Journal on Computing, 1972, 1 (2): 146–160, doi:10.1137/0201010
Aspvall, Bengt; Plass, Michael F.; Tarjan, Robert E., , Information Processing Letters, 1979, 8 (3): 121–123, doi:10.1016/0020-0190(79)90002-4.
Dulmage, A. L. & Mendelsohn, N. S., , Can. J. Math., 1958, 10: 517–534, S2CID 123363425, doi:10.4153/cjm-1958-052-0.

外部链接

Aspvall, Bengt; Plass, Michael F.; Tarjan, Robert E., , Information Processing Letters, 1979, 8 (3): 121–123, doi:10.1016/0020-0190(79)90002-4.
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 22.5, pp. 552–557.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 22.5, pp. 552–557.

[2] Sharir, Micha, , Computers & Mathematics with Applications, 1981, 7: 67–72, doi:10.1016/0898-1221(81)90008-0 

[3] Tarjan, R. E., , SIAM Journal on Computing, 1972, 1 (2): 146–160, doi:10.1137/0201010

[4] Aspvall, Bengt; Plass, Michael F.; Tarjan, Robert E., , Information Processing Letters, 1979, 8 (3): 121–123, doi:10.1016/0020-0190(79)90002-4.

[5] Dulmage, A. L. & Mendelsohn, N. S., , Can. J. Math., 1958, 10: 517–534, S2CID 123363425, doi:10.4153/cjm-1958-052-0.