轉動慣量
在经典力學中,轉動慣量又稱慣性矩(英語:),通常以[1]表示,國際單位制為。轉動慣量是一個物體對於其旋轉運動的慣性大小的量度。一個剛體對於某轉軸的轉動慣量決定對於這物體繞著這轉軸進行某種角加速度運動所需要施加的力矩。
| 轉動慣量 | |
|---|---|
常見符號 | I |
| 国际单位 | kg m2 |
其他單位 | lbf·ft·s2 |
| 單位因次 | M L2 |
從其他物理量的推衍 | |
| 因次 | M L2 |

相关概念
定轴转动动能
一般物件的動能是。將速度和質量,用轉動力學的定義取代:
- ,
得出
- ,
簡化得
- 。
如果一個人坐在一張可轉動的椅子,雙手拿重物,張開雙手,轉動椅子,然後突然將手縮到胸前,轉動的速度將突然增加,因為轉動慣量減少了。
常用定理
平行軸定理
平行軸定理是說,如果一個質量為的物件,以某條經過质心點的直線為軸,其轉動慣量為。在空間取點,使得垂直於原本的軸。那麼如果以經過、平行於原本的軸的直線為軸,的距離為,則。
垂直轴定理
垂直轴定理是说,如果一个平面物件,以该平面内两条互相垂直、交于点的直线为轴,转动惯量分别为、,则它以过点且垂直于该平面的直线为轴的转动惯量。
伸展定则
伸展定则是说,如果一个物件中的任一质点沿平行于某条轴的方向发生任意位移,该物件对该轴的转动惯量不变。
慣性張量
對於三維空間中任意一参考點與以此参考點為原點的直角坐標系,一個剛體的慣性張量是
- 。(1)
這裏,矩陣的對角元素、、分別為對於-軸、-軸、-軸的轉動慣量。設定為微小質量對於點的相對位置。則這些轉動慣量以方程式定義為
- ,
- ,(2)
- 。
矩陣的非對角元素,稱為慣量積,以方程式定義為
- ,
- ,(3)
- 。
導引
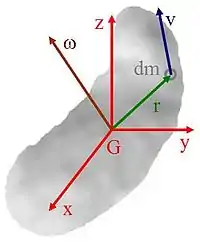
如圖,一個剛體對於質心與以點為原點的直角座標系的角動量定義為
- 。
這裏,代表微小質量在座標系的位置,代表微小質量的速度。因為速度是角速度叉積位置,所以,
- 。
計算-軸分量,
相似地計算-軸與-軸分量,角動量為
- ,
- ,
- 。
如果,我們用方程式(1)設定對於質心的慣性張量,讓角速度為,那麼,
- 。(4)
平行軸定理
平行軸定理能夠很簡易的,從對於一個以質心為原點的座標系統的慣性張量,轉換至另外一個平行的座標系統。假若已知剛體對於質心的慣性張量,而質心的位置是,則剛體對於原點的慣性張量,依照平行軸定理,可以表述為
- ,
- ,(5)
- ,
- ,
- ,(6)
- 。
證明:
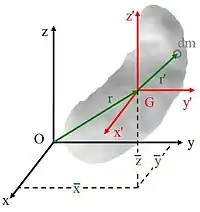
a)參考圖B,讓、分別為微小質量對質心與原點的相對位置:
- ,。
依照方程式(2),
- 。
所以,
相似地,可以求得、的方程式。
b)依照方程式(3),
- 。
- 。
因為,,所以
相似地,可以求得對於點的其他慣量積方程式。
對於任意軸的轉動慣量
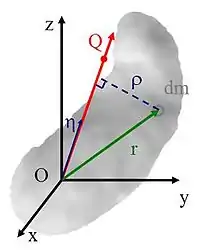
參視圖C,設定點為直角座標系的原點,點為三維空間裏任意一點,不等於。思考一個剛體,對於-軸的轉動慣量是
- 。
這裏,是微小質量離-軸的垂直距離,是沿著-軸的單位向量,是微小質量的位置。
展開叉積,
- 。
稍微加以編排,
特別注意,從方程式(2)、(3),這些積分項目,分別是剛體對於-軸、-軸、-軸的轉動慣量與慣量積。因此,
- 。(7)
如果已經知道,剛體對於直角座標系的三個座標軸,-軸、-軸、-軸的轉動慣量。那麼,對於-軸的轉動慣量,可以用此方程式求得。
參考文獻
- 普通物理学(修订版,化学数学专业用)。汪昭义主编。华东师范大学出版社.P81.三、转动惯量.ISBN 978-7-5617-0444-8/N·018
- O'Nan, Michael. . USA: Harcourt Brace Jovanovich, Inc. 1971: pp。361. ISBN 0-15-518558-6 (英语).
- Beer, Ferdinand; E. Russell Johnston, Jr., William E. Clausen (2004). Vector Mechanics for Engineers. 7th edition. USA: McGraw-Hill, ISBN 978-0-07-230492-3
外部連結
- 轉動Java模擬 (页面存档备份,存于)
- 平衡垂直棒子Java模擬 (页面存档备份,存于)
- 教育部進修網站,慣性矩