星形十二面體

在幾何學中，星形十二面體是指正十二面體的星形化體，即把正十二面體的面和邊沿伸直到向外相交成星形的立體。溫尼爾在他的書《多面體模型》中列出許多星形多面體模型，其中也收錄了一些星形十二面體[1]。目前已知共有三種星形十二面體[2]，部分文獻列出的正十二面體星形化體共有四種，其中包括了正十二面體本身和三種星形多面體，這三種都是正多面體，並且皆已被命名，其中有2種出現於藝術創作中，一種是大十二面體，出現於榎宮祐於2012年創作的小說《NO GAME NO LIFE 遊戲人生》中[3]，另一種是小星形十二面體，分別出現於莫里茲·柯尼利斯·艾雪於1950年創作的《Contrast (Order and Chaos)》以及1952年創作的《引力》中[4]、和保羅·烏切洛於1430年在威尼斯聖馬爾谷聖殿宗主教座堂創作的鑲嵌藝術中。

  此条目页的主題是正十二面體的星形化體。与「星形十二面體」標題相近或相同的条目页，請見「星形十二面體 (消歧義)」。
星形十二面體
部分的星形十二面體
小星形十二面體
小星形十二面體
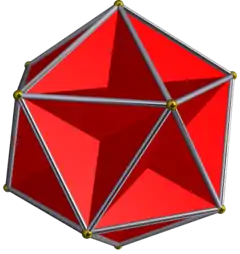大十二面體
大十二面體		 大星形十二面體
大星形十二面體

組成
星形十二面體為正十二面體面向外延伸的結果。

星形十二面體是指正十二面體的星形化體，其為將正十二面體的五邊形面向外延伸直到相交成為星形的立體，第一次相交會形成五角星形狀的立體，稱為小星形十二面體；第二次向外延伸為將五角星凹處向外延伸直到變為五邊形，所形成的立體為大十二面體；第三次延伸即為第二次延伸結果的五邊形向外延伸成五角星，所形成的立體為大星形十二面體。每次延伸結果多出來的部分都稱為星形十二面體的一個胞，在星狀圖中以兩個的五角星，其中一個嵌入另一個五角星內部的圖案表示[5]。

種類

正十二面體透過胞規則可以產生4種星形十二面體[6]；全部匹配則能產生的星形十二面體同樣僅有4種[6]，透過米勒的規則[7]可以亦同[6]，其中這4種包括了正十二面體本身和3種星形多面體。[8]

列表
名稱 對稱群 圖像 星狀圖
原像 正十二面體（正圖形） Ih
第一種 小星形十二面體（正圖形）
（第一種星形十二面體）		 Ih
第二種 大十二面體（正圖形）
（第二種星形十二面體）		 Ih
第三種 大星形十二面體（正圖形）
（第三種星形十二面體）		 Ih

文化影響

星形十二面體的創作最早出現於文藝復興時期的藝術中。在意大利聖馬爾谷聖殿宗主教座堂的地板上，有以鑲嵌藝術的方式在大理石的焦油石中描繪的小星形十二面體，通常被認為是1430年由保羅·烏切洛所創作。1568年溫佐·雅姆尼策爾發表了一個木刻作品《Perspectiva Corporum Regularium》，中描繪了一個大十二面體和大星形十二面體。[9]

在近代，星形十二面體亦有出現於文化中，例如莫里茲·柯尼利斯·艾雪於1950年創作的《Contrast (Order and Chaos)》以及1952年創作的《引力》中[4]。亞當．亞歷山大於1982年發明的一種魔方——亚历山大之星外型也是一種星形十二面體[9][10]，榎宮祐於2012年創作的小說《NO GAME NO LIFE 遊戲人生》中，唯一神持有的稱作星杯之象徵物件也是以星形十二面體做為外型[3]；挪威藝術家Vebjørn Sand於在加勒穆恩奧斯陸機場展出的雕塑《The Kepler Star》是星形十二面體中的大星形十二面體、正二十面體和正十二面體的複合圖形[9]。不過從這些藝術創作中無法得知藝術家是否真的具備相關幾何學知識。[9]

星形五角十二面體

星形五角十二面體是指五角十二面體的星形化體。布拉托夫在其研究中列出了270種星形五角十二面體。[11][8]

參見

參考文獻
  1. Wenninger, Magnus. . Cambridge University Press. 1974. ISBN 0-521-09859-9.
  2. George Hart. . georgehart.com. [2019-09-06]. （原始内容存档于2018-11-30）.
  3. 榎宮祐. . 2014-04-25: 第330-331頁. EAN 4710945544663.
  4. Locher, J. L. (2000). The Magic of M. C. Escher. Harry N. Abrams, Inc. ISBN 0-8109-6720-0
  5. Jim Wilson. . Mathematics Education, The University of Georgia. 2016-07-20 [2019-10-23]. （原始内容存档于2017-06-03）.
  6. Webb, R. . software3d.com. [2019-09-06]. （原始内容存档于2019-04-27）.
  7. Guy's. . steelpillow.com. 2010-12-19 [2016-03-26]. （原始内容存档于2016-03-04）.
  8. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
  9. Jim Wilson. . Mathematics Education, The University of Georgia. 2016-07-20 [2019-10-23]. （原始内容存档于2017-03-30）.
  10. Jaap Scherphuis. . [2019-10-23]. （原始内容存档于2018-04-11）.
  11. V. Bulatov. . 1997 [2019-10-11]. （原始内容存档于2018-01-31）.

外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.