耿贝尔分布
在概率论和统计学中,耿贝尔分布(Gumbel分布,也称为I 型广义极值分布)用于对各种分布的多个样本的最大值(或最小值)的分布进行建模。
|
密度函數 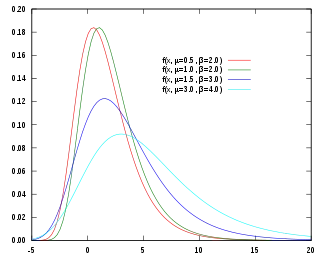 | |||
|
累積分布函數 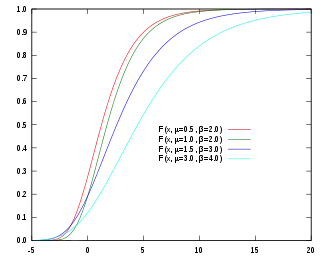 | |||
| 记号 | |||
|---|---|---|---|
|
location (real) scale (real) | |||
| 值域 | |||
|
其中 | |||
| 累積分布函數 | |||
| 期望值 |
其中是Euler–Mascheroni常数 | ||
| 中位數 | |||
| 眾數 | |||
| 偏度 | |||
| 峰度 | |||
| 熵 | |||
| 特徵函数 | |||
如果有过去十年的水位最大值列表,则此分布可用于表示特定年份河流最高水位的分布。它有助于预测发生极端地震、洪水或其他自然灾害的可能性。 耿贝尔分布表示最大值分布的潜在适用性与极值理论有关,这表明如果基础样本数据的分布是正态或指数类型,它可能是有用的。本文使用耿贝尔分布对最大值的分布进行建模。要对最小值建模,请使用原始值的负值。
耿贝尔分布是广义极值分布(也称为 Fisher-Tippett 分布)的一个特例。它也称为对数Weibull 分布和双指数分布(该术语有时也用于指代拉普拉斯分布)。它与Gompertz分布有关:在原点附近,并限制在正半线上时,就得到了 Gompertz 函数。
在多项式logistic回归模型的潜变量公式中——在离散选择法理论中很常见——潜在变量的误差服从 Gumbel 分布。这很有用,因为两个耿贝尔分布的随机变量的差服从logistic分布。
耿贝尔分布以Emil Julius Gumbel (1891 – 1966) 的名字命名,来自描述该分布的原始论文。 [1] [2]
相关分布
- 如果具有耿贝尔分布,则Y= − X的条件分布在Y为正的情况下,或等效地在X为负的情况下具有Gompertz分布。 Y的 cdf G与X的 cdf F相关,公式如下要求y > 0。因此,两者概率密度函数相关: : Gompertz 密度与反射的 Gumbel 密度成正比,仅限于正半线。 [4]
- 如果X是均值为 1 的指数分布变量,则− log( X ) 服从标准 Gumbel 分布。
- 如果和是独立的,那么 (见Logistic分布)。
- 如果是独立的,那么 。注意 。更一般地,独立 Gumbel 随机变量的线性组合的分布可以用 GNIG 和 GIG 分布来近似。 [5]
与广义多变量对数伽马分布相关的理论提供了耿贝尔分布的多变量版本。
应用
Gumbel 表明,随着样本量的增加,将服从指数分布的随机变量减去样本量[7]的自然对数,其最大值的分布(或最后一阶统计量)接近耿贝尔分布。 [8]
具体来说,如果令是的概率分布,是其累积分布,那么对的次实现(realizations)的最大值小于当且仅当所有的实现都小于 。所以最大值的累积分布满足:
并且,对于较大的,等式右边收敛到。
因此,在水文学中,耿贝尔分布用于分析日降雨量和河流流量的月度和年度最大值等变量, [3]也用于描述干旱。 [9]
Gumbel 还表明,表示事件的概率的估计量r⁄(n+1)——其中r是观察值在数据序列中的排名, n是观察的总数——是分布的众数周围的累积分布函数的无偏估计量。因此,这个估计量经常被用作分位图。
随机变量生成
耿贝尔分布的分位数函数(逆累积分布函数) 可由下式给出
其中和是参数,当随机变量是从 上的均匀分布中抽取时,变量具有服从耿贝尔分布。
概率纸

在软件时代之前,人们使用概率纸描绘耿贝尔分布(见插图)。这种纸基于累积分布函数的的线性化:
在纸上,水平轴以双对数刻度构建。垂直轴是线性的。通过在纸张的水平轴上寻找,在垂直轴上寻找 ,耿贝尔分布由斜率为 的直线表示。当像CumFreq这样的分布拟合软件可用时,绘制分布的任务变得更加容易。
参见
- 2型Gumbel分布
- 极值理论
- 广义极值分布
- Fisher-Tippett-Gnedenko定理
- 埃米尔·朱利叶斯·冈贝尔
参考资料
- Gumbel, E.J., (PDF), Annales de l'Institut Henri Poincaré, 1935, 5 (2): 115–158 [2023-01-21], (原始内容存档 (PDF)于2018-03-10)
- Gumbel E.J. (1941). "The return period of flood flows". The Annals of Mathematical Statistics, 12, 163–190.
- Oosterbaan, R.J. http://www.waterlog.info/pdf/freqtxt.pdf
|chapterurl=缺少标题 (帮助) (PDF). Ritzema, H.P. (编). . Wageningen, The Netherlands: International Institute for Land Reclamation and Improvement (ILRI). 1994: 175–224. ISBN 90-70754-33-9. - Willemse, W.J.; Kaas, R. (PDF). Insurance: Mathematics and Economics. 2007, 40 (3): 468 [2023-01-21]. doi:10.1016/j.insmatheco.2006.07.003. (原始内容 (PDF)存档于2017-08-09).
- Marques, F.; Coelho, C.; de Carvalho, M. (PDF). Statistics and Computing. 2015, 25: 683‒701 [2023-01-21]. doi:10.1007/s11222-014-9453-5. (原始内容存档 (PDF)于2022-12-20).
- CumFreq, software for probability distribution fitting
- . [2023-01-21]. (原始内容存档于2021-08-26).
- Gumbel, E.J. . Applied Mathematics Series 33 1st. U.S. Department of Commerce, National Bureau of Standards. 1954 [2023-01-21]. ASIN B0007DSHG4. (原始内容存档于2023-01-21).
- Burke, Eleanor J.; Perry, Richard H.J.; Brown, Simon J. . Journal of Hydrology. 2010, 388 (1–2): 131–143. Bibcode:2010JHyd..388..131B. doi:10.1016/j.jhydrol.2010.04.035.
- Erdös, Paul; Lehner, Joseph. . Duke Mathematical Journal. 1941, 8 (2): 335. doi:10.1215/S0012-7094-41-00826-8.
- Kourbatov, A. . Journal of Integer Sequences. 2013, 16. Bibcode:2013arXiv1301.2242K. arXiv:1301.2242
 . Article 13.5.2.
. Article 13.5.2. - Jang, Eric; Gu, Shixiang; Poole, Ben. . International Conference on Learning Representations (ICLR) 2017. April 2017 [2023-01-21]. (原始内容存档于2023-01-21).
- Balog, Matej; Tripuraneni, Nilesh; Ghahramani, Zoubin; Weller, Adrian. . International Conference on Machine Learning (PMLR). 2017-07-17: 371–379 [2023-01-21]. (原始内容存档于2023-01-21) (英语).
