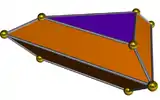
雙三角錐柱
雙三角錐柱是指以三角形為基底的雙角錐柱,其可以由三角柱在兩端各連接一個三角錐來構成。若雙三角錐柱的基底為正三角形,且側面都是正多邊形的話,則這個立體是一種全部由正多邊形組成的立體,為92種詹森多面體中的其中一個,其索引為J14[1]。詹森多面體是凸多面體,面皆由正多邊形組成但不屬於均勻多面體,共有92種。這些立體最早在1966年由諾曼·詹森(Norman Johnson)命名並給予描述[2]。
 | ||||
| 類別 | 詹森多面體 J13 - J14 - J15 | |||
|---|---|---|---|---|
| 對偶多面體 | 雙三角錐台 | |||
| 識別 | ||||
| 名稱 | 雙三角錐柱 | |||
| 參考索引 | J14 | |||
| 鮑爾斯縮寫 | etidpy | |||
| 數學表示法 | ||||
| 康威表示法 | k3P3 | |||
| 性質 | ||||
| 面 | 9 | |||
| 邊 | 15 | |||
| 頂點 | 8 | |||
| 歐拉特徵數 | F=9, E=15, V=8 (χ=2) | |||
| 組成與佈局 | ||||
| 面的種類 | 6個三角形 3個正方形 | |||
| 頂點圖 | 2(33) 6(32.42) | |||
| 對稱性 | ||||
| 對稱群 | D3h, [3,2], (*322) | |||
| 圖像 | ||||
| ||||
nirrosula是一種由植物葉子條編織而成的非洲樂器,由一系列細長的雙角錐柱製成,其端蓋的面為不等邊三角形,也就是非正的雙三角錐柱外型的樂器。[3]
性質
雙三角錐柱共由9個面、15條邊和8個頂點組成[4][5][6],在其9個面中,有6個三角形面和3個正方形面[4]。在其8個頂點中,有兩種頂點,一種頂點為3個三角形的公共頂點,在頂點圖中可以用[33]來表示[7],這種頂點有2個[6]、另外一種頂點為2個三角形和2個正方形的公共頂點,在頂點圖中可以用[32,42]來表示[7],這種頂點有6個[6]。
參考文獻
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Johnson, Norman W., , Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8.
- Gerdes, Paulus, , ZDM, the International Journal on Mathematics Education, 2009, 42 (1): 11–17, doi:10.1007/s11858-009-0208-2.
- David I. McCooey. . [2022-09-07]. (原始内容存档于2022-09-07).
- . qfbox.info. [2022-09-07]. (原始内容存档于2022-09-07).
- . polyhedra.tessera.li. [2022-09-07]. (原始内容存档于2022-09-07).
- Richard Klitzing. . bendwavy.org. [2022-09-07]. (原始内容存档于2022-11-14).
- Wolfram, Stephen. . from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- Sapiña, R. . Problemas y ecuaciones. [2020-09-04]. ISSN 2659-9899. (原始内容存档于2020-09-30) (西班牙语).
- David I. McCooey. . [2022-09-07]. (原始内容存档于2022-09-07).
- David I. McCooey. . [2022-09-07]. (原始内容存档于2019-08-22).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.