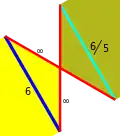
六邊形半無限邊形鑲嵌
六邊形半無限邊形鑲嵌(hexagonal hemiapeirogonal tesselation)是一種平面鑲嵌圖,由六邊形和無限邊形組成。[1]其外觀與截半六邊形鑲嵌相似,差別在於截半六邊形鑲嵌有三角形面和六邊形面,而六邊形半無限邊形鑲嵌在外觀上僅有六邊形面,剩餘的三角形為孔洞。[2]這個幾何結構可以視為半多面體的一種廣義的形式。[3][1]
 | ||
| 類別 | 均勻星形鑲嵌圖 | |
|---|---|---|
| 識別 | ||
| 名稱 | 六邊形半無限邊形鑲嵌 hexagonal hemiapeirogonal tesselation | |
| 鮑爾斯縮寫 | hoha | |
| 數學表示法 | ||
| 威佐夫符號 | 6/5 6 | ∞ | |
| 組成與佈局 | ||
| 面的種類 | 六邊形 無限邊形 | |
| 頂點圖 | ∞.6.∞.6/5 | |
| 對稱性 | ||
| 對稱群 | p6m | |
| 圖像 | ||
| ||
雙六邊形半無限邊形鑲嵌
六邊形半無限邊形鑲嵌並不滿足格林鮑姆鑲嵌圖的特性。若要滿足格林鮑姆鑲嵌圖的特性,所有元素都必須要位於重合對中,因此考慮到結構中的三角形孔洞,需要將每個頂點的六邊形配置為交替並環繞頂點兩圈的形式來構造,如此以來這個立體結構中每個六邊形的位置上都會存在一對重合的六邊形。[6]
相關多面體與鑲嵌
六邊形半無限邊形鑲嵌與截半六邊形鑲嵌和三角形半無限邊形鑲嵌共用相同的頂點排列。[7][2]
 截半六邊形鑲嵌與三角形半無限邊形鑲嵌和六邊形半無限邊形鑲嵌的頂點排列
截半六邊形鑲嵌與三角形半無限邊形鑲嵌和六邊形半無限邊形鑲嵌的頂點排列.svg.png.webp)
 六邊形半無限邊形鑲嵌與雙六邊形半無限邊形鑲嵌
六邊形半無限邊形鑲嵌與雙六邊形半無限邊形鑲嵌
六邊形半無限邊形鑲嵌由六邊形和無限邊形組成。而六邊形本身也能構成鑲嵌圖,即正六邊形鑲嵌,然而正六邊形鑲嵌的頂點排列方式與六邊形半無限邊形鑲嵌並不相同。六邊形半無限邊形鑲嵌的廣義凸包對應到的是截半六邊形鑲嵌[2]而非正六邊形鑲嵌。[8]而同時與正六邊形鑲嵌、無限邊形相關的幾何結構為皮特里六邊形鑲嵌,然而在皮特里六邊形鑲嵌中構成的無限邊形並非一般的無限邊形,而是扭歪無限邊形。[9]
註釋
參考文獻
- Grünbaum, Branko; Shephard, G. C. . W. H. Freeman and Company. 1987. ISBN 0-7167-1193-1. (Star tilings section 12.3)
- Richard Klitzing. . 3D convex uniform polyhedra. bendwavy. [2021-10-16]. (原始内容存档于2021-09-24).
- Jim McNeill. . orchidpalms.com. [2021-08-01]. (原始内容存档于2020-02-25).
- . dmccooey.com. [2021-08-01]. (原始内容存档于2021-07-30).
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P., , Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society), 1954, 246 (916): 401–450, ISSN 0080-4614, JSTOR 91532, MR 0062446, doi:10.1098/rsta.1954.0003
- Richard Klitzing. . 3D convex uniform polyhedra. bendwavy. [2021-10-16]. (原始内容存档于2021-09-24).
- Richard Klitzing. . 3D convex uniform polyhedra. bendwavy. [2021-09-06]. (原始内容存档于2021-09-24).
- Richard Klitzing. . 3D convex uniform polyhedra. bendwavy. [2021-10-16]. (原始内容存档于2022-04-08).
- McMullen, P., Schulte, E. . Discrete & Computational Geometry. 1997-06-01, 17 (4): 449-478 [2021-09-06]. ISSN 1432-0444. doi:10.1007/PL00009304. (原始内容存档于2018-06-03).
- Andreas W. M. Dress. . Aequationes Mathematicae. 1985-12, 29 (1): 222–243 [2021-09-24]. ISSN 0001-9054. doi:10.1007/BF02189831. (原始内容存档于2021-09-26) (英语).
外部連結
- 關於皮特里三角形鑲嵌,可參考YouTube上的《普通空間中的48種正多面體》(英文)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.