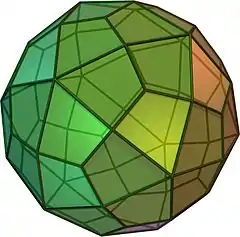
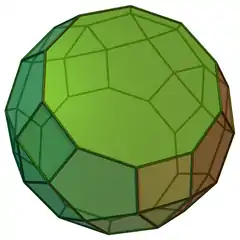
小斜方截半二十面体
在幾何學中,小斜方截半二十面體是一種半正多面體,由於其具有點可遞的性質,因此屬於阿基米德立體[1]。它由20個正三角形面、30個正方形面、12個正五邊形面、60個頂點和120條棱構成[2]。其對偶多面體為鳶形六十面體[3]。
 (按這裡觀看旋轉模型) | |||||
| 類別 | 半正多面體 | ||||
|---|---|---|---|---|---|
| 對偶多面體 | 鳶形六十面體 | ||||
| 識別 | |||||
| 名稱 | 小斜方截半二十面体 | ||||
| 參考索引 | U27, C30, W14 | ||||
| 鮑爾斯縮寫 | srid | ||||
| 數學表示法 | |||||
| 考克斯特符號 | |||||
| 施萊夫利符號 | rr{5,3} | ||||
| 威佐夫符號 | 3 5 | 2 | ||||
| 康威表示法 | eD aaD | ||||
| 性質 | |||||
| 面 | 62 | ||||
| 邊 | 120 | ||||
| 頂點 | 60 | ||||
| 歐拉特徵數 | F=62, E=120, V=60 (χ=2) | ||||
| 組成與佈局 | |||||
| 面的種類 | 正三角形 正方形 正五邊形 | ||||
| 面的佈局 | 20個{3} 30個{4} 12個{5} | ||||
| 頂點圖 | 3.4.5.4 | ||||
| 對稱性 | |||||
| 對稱群 | Ih群 | ||||
| 特性 | |||||
| - | |||||
| 圖像 | |||||
| |||||
命名
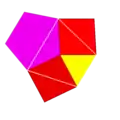
约翰内斯·开普勒在他1618年出版的《世界的和諧》中,將這個多面體命名為小斜方截半二十面體(rhombicosidodecahedron),可以看做是截角截半二十面體菱形(truncated icosidodecahedral rhombus)的縮寫,由於小斜方截半二十面體可以看做是菱形三十面體透過截角變換後的像而得名,其中截半二十面體菱形(icosidodecahedral rhombus)是开普勒給予菱形三十面體的命名[4]。 菱形三十面體透過截角變換後的像在拓樸學上可以產生兩種不同的幾何形狀:左邊為最直接的截半;中間是在五階頂點截的較深的截半,其形成了均勻多面體;右邊的是小斜方截半二十面體與菱形三十面體的對偶多面體——截半二十面体的複合體。
性質

小斜方截半二十面體是一種半正多面體,由三種正多邊形組成,分別為正三角形面、正方形面和正五邊形,每個頂點都是兩個正方形、一個正三角形和一個五邊形的公共頂點,在頂點圖中可計為3.4.5.4,因此具有點可遞的性質。由於其可以藉由正十二面體透過擴展變換,變換而成,因此又可以稱為擴展十二面體。由於此原因,小斜方截半二十面體在施萊夫利符號中可以用rr{5,3}來表示,其中,rr表示擴展變換,{5,3}表示正十二面體,亦可以簡寫為[5]。
幾何關聯
将一个正十二面体(正二十面体)三十条棱都切一刀,在二十(十二)个顶点处也切一刀,就可以得到一个小斜方截半二十面体。也可以透過將正二十面体移動到遠離原點適當的距離,並且不改變面的大小,然後對偶多面體(正十二面体)也做相同動作,並且在剩餘的空隙補上正方形也可以得到小斜方截半二十面体。一可以視為截半二十面體再次截半後的像[6]。因此,小斜方截半二十面体具有與正二十面體相同數量的三角形和與正十二面體相同數量的五邊形,且正方形恰好等於正二十面體或正十二面體邊的數量。
 小斜方截半二十面體 |
 小十二面截半二十面體 |
 小斜方十二面體 |
 小星形截角十二面體 |
 六複合五角星柱 |
 十二複合五角星柱 |
小斜方截半二十面體與小星形截角十二面體、六複合五角星柱以及十二複合五角星柱共用相同的頂點布局。
其他特性
小斜方截半二十面體由上而下可以分成5層,如下圖所示,靠近頂面的那層可形成一個正十邊形,特別地,由於其對稱性,因此每十條棱皆可以成為一個正十邊形,整個小斜方截半二十面體共有十二個獨立的十邊形。
 小斜方截半二十面體的上下分层着色 |
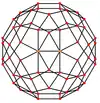
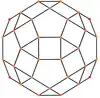
正交投影
小斜方截半二十面體有6個特殊的正交投影,分別為於中心投影、於頂點上投影、於稜上投影(兩種)和於面上投影(三種),其中「在正方形面上投影」以及「在正五邊形面上投影」其對稱性對應於A2 和 H2的考克斯特平面[9]。
| 投影位置 | 頂點 | 三角形-正方形 稜 |
五邊形-正方形 稜 |
正方形面 | 三角形面 | 五邊形面 |
|---|---|---|---|---|---|---|
| 立體圖 |  |
 |
 | |||
| 骨架 |  |
 |
 |
 |
 |
 |
| 投影 對稱性 |
[2] | [2] | [2] | [2] | [6] | [10] |
| 對偶骨架 |  |
 |
 |
 |
 |
 |
球面鑲嵌
小斜方截半二十面體也可以表示為球面鑲嵌,並通過球極投影,投影到平面上。 這個投影是一個等角頭影,雖然長度發生改變,但保留了角度資訊。 球面鑲嵌上的直線投影到了平面後成為了弧線。
 |
 以正五邊形為中心 |
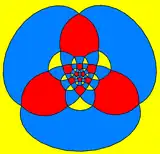 以正三角形為中心 |
 以正方形為中心 |
| 正交投影 | 球極平面投影 | ||
|---|---|---|---|
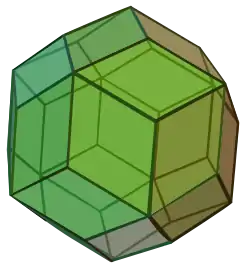
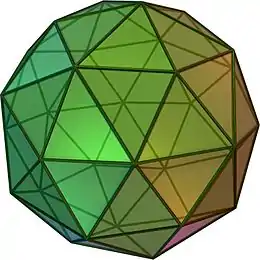
相關多面體與鑲嵌

小斜方截半二十面體是正十二面體經過擴展變換後的結果,其他也是由正二十面體透過康威變換得到的多面體有:
| 對稱群: [5,3], (*532) | [5,3]+, (532) | ||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 | |
| {5,3} | t0,1{5,3} | t1{5,3} | t0,1{3,5} | {3,5} | t0,2{5,3} | t0,1,2{5,3} | s{5,3} |
| 半正多面体对偶 | |||||||
 |
 |
 |
 |
 |
 | ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
參考文獻
- Williams, Robert. . Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
- Cromwell, P. . United Kingdom: Cambridge. 1997: 79–86 Archimedean solids. ISBN 0-521-55432-2.
- The Big Bang Theory Series 8 Episode 2 - The Junior Professor Solution: features this solid as the answer to an impromptu science quiz the main four characters have in Leonard and Sheldon's apartment, and is also illustrated in Chuck Lorre's Vanity Card #461 at the end of that episode.
- Cromwell, P. Polyhedra, CUP hbk (1997), pbk. (1999). Ch.2 p.79-86 Archimedean solids
- . bulatov.com. [2018-08-27]. (原始内容存档于2017-10-11).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Harmonies Of The World by Johannes Kepler, Translated into English with an introduction and notes by E. J. Aiton, A. M. Duncan, "J. V. Field, 1997, ISBN 0-87169-209-0 (page 123)
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- . The Geometry Center. [2018-08-27]. (原始内容存档于2016-12-04).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- . dmccooey.com. [2018-08-27]. (原始内容存档于2018-01-29).
- Coxeter Planes (页面存档备份,存于) and More Coxeter Planes (页面存档备份,存于) 約翰·史坦布里奇
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
外部連結
- 埃里克·韦斯坦因, 小斜方截半二十面体 (參閱阿基米德立體) 於MathWorld(英文)
- Klitzing, Richard. . bendwavy.org.
- Editable printable net of a Rhombicosidodecahedron with interactive 3D view (页面存档备份,存于)
- The Uniform Polyhedra (页面存档备份,存于)
- Virtual Reality Polyhedra (页面存档备份,存于) The Encyclopedia of Polyhedra
- The Rhombi-Cosi-Dodecahedron Website (页面存档备份,存于)
- The Rhombicosidodecahedron as a 3D puzzle