三角形
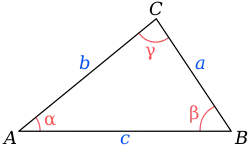
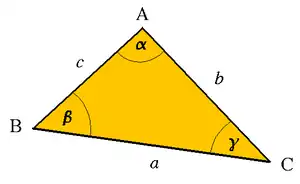
三角形,又稱三邊形(英語: Triangle),是由三条线段顺次首尾相连,或不共線的三點兩兩連接,所组成的一个闭合的平面几何图形,是最基本和最少邊的多边形。
| 三角形(英語: Triangle) | |
|---|---|
 三角形 | |
| 邊 | 3 |
| 頂點 | 3 |
| 施萊夫利符號 | {3}(正三角形時) |
| 鮑爾斯縮寫 | trig |
| 面積 | 有各種求面積的公式; 見#面積一節 |
| 內角和 | 一百八十度 |
分类
以角度分類
 |
 |
 |
| 锐角三角形 | 钝角三角形 | 直角三角形 |
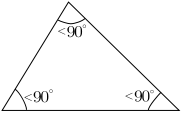
锐角三角形
銳角三角形的所有內角均為銳角。
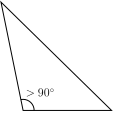
钝角三角形
鈍角三角形是其中一角為鈍角的三角形,其余兩角均小於90°。
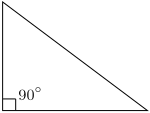
直角三角形
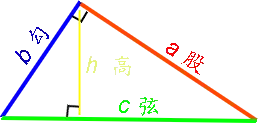
有一个角是直角(90°)的三角形为直角三角形。成直角的两条边称为「直角邊」(cathetus),直角所对的边是「斜邊」(hypotenuse);或最長的邊稱為「弦」,底部的一邊稱作「勾」(又作「句」),另一邊稱為「股」。斜邊乘上斜邊上的高÷2=勾股相乘÷2=此直角三角形面積(ch=ab)
三角函数
直角三角形各邊與角度的關係,可以三角比表示。
以邊長分類
 |
 |
 |
| 不等邊三角形 | 等邊三角形 | 等腰三角形 |
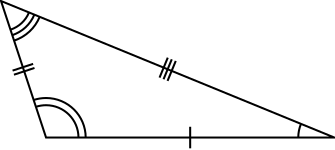
不等邊三角形
三條邊邊長皆不相等的三角形稱為不等邊三角形。
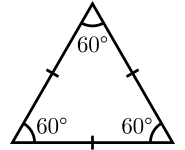
等邊三角形
等邊三角形(又称正三角形),为三边相等的三角形。其三個內角相等,均為60°。它是銳角三角形的一種。设其边长是 ,则其面積公式為 。
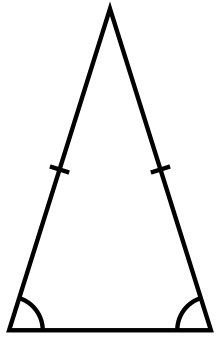
等腰三角形
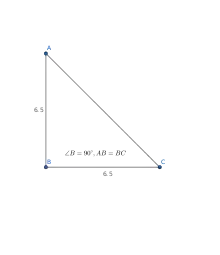
等腰三角形是三条边中有两条边相等(或是其中兩隻內角相等)的三角形。等腰三角形中的两条相等的边被称为「腰」,而另一条边被称为「底边」,两条腰交叉组成的那个点被称为「顶点」,它们组成的角被称为「顶角」。
等边三角形和等腰直角三角形是等腰三角形的特殊形式。
令其底边是 ,腰是 ,则其面積公式為 等腰三角形的对应高,角平分线和中线重合。
退化三角形
退化三角形是指面積為零的三角形。满足下列条件之一的三角形即可称为退化三角形:三个内角的度数为(180°,0°,0°)或(90°,90°,0°);三边其中一条边的长度为0;一条边的长度等于另外两条之和。有人认为退化三角形并不能算是三角形,這是由於它介乎於三角不等式之間,在一些資料中已否定了其中一條邊等於其餘兩條邊之和的情況。
勒洛三角形
勒洛三角形(英語:),也譯作萊洛三角形或弧三角形,又被稱為劃粉形或曲邊三角形,是除了圓形以外,最簡單易懂的勒洛多邊形,一個定寬曲線。將一個曲線圖放在兩條平行線中間,使之與這兩平行線相切,則可以做到:無論這個曲線圖如何運動,只要它還是在這兩條平行線內,就始終與這兩條平行線相切。這個定義由十九世紀的德國工程師弗朗茨·勒洛命名。
一般性质
三角不等式
- 三角边長不等式
- 三角形两边之和大于第三边,两边之差的绝对值小于第三边。如果兩者相等,则是退化三角形。
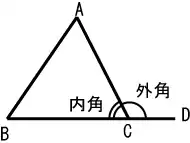
- 三角內外角不等式
- 三角形任意一个外角大于不相邻的一个内角。
全等及相似
全等三角形
三角形具有穩定性,若二個三角形有以下的邊角關係確定後,它的形狀、大小就不會改變,二個三角形即為全等三角形。全等三角形的判斷準則有以下幾種:
- SSS(Side-Side-Side,邊、邊、邊):各三角形的三條邊的長度都對應地相等。
- SAS(Side-Angle-Side,邊、角、邊):各三角形的其中兩條邊的長度都對應地相等,且兩條邊夾著的角都對應地相等。
- ASA(Angle-Side-Angle,角、邊、角):各三角形的其中兩個角都對應地相等,且兩個角夾著的邊都對應地相等。
- RHS(Right Angle-Hypotenuse-Side,直角、斜邊、邊):在直角三角形中,斜邊及另外一條直角邊對應地相等。[1]
- AAS(Angle-Angle-Side,角、角、邊):各三角形的其中兩個角都對應地相等,且其中一組對應角的對邊也對應地相等。
SSA(Side-Side-Angle、邊、邊、角)不能保证两个三角形全等,除非該角大於等於90°,此時可以保證全等。[2]:34[3]
相似三角形
- AA(Angle-Angle,角、角):各三角形的其中兩個角的都對應地相等。(或稱AAA(Angle-Angle-Angle,角、角、角))
- 三邊成比例(3 sides proportional):各三角形的三條邊的長度都成同一比例。
- 兩邊成比例且夾角相等(ratio of 2 sides, inc.∠):各三角形的兩條邊之長度都成同一比例,且兩條邊之夾角都對應地相等。(或稱 2 sides proportional, inc. ∠ equal)
特殊線段
三角形中有著一些特殊線段,是三角形研究的重要對象。
- 中線(median):三角形一边中点与这边所对頂点的连线段。
- 高线(altitude):从三角形一个顶点向它的对边所作的垂线段。
- 角平分线(angle bisector):平分三角形一角、一个端点在这一角的对边上的线段。
- 垂直平分線(perpendicular bisector):通過三角形一边中点与該边所垂直的线段,又稱中垂线。
以上特殊線段,每個三角形均有三條,且三線共點。
中线长度
设在中,若三边、、的中線分别为、、,则:
高线长度
设在中,連接三个顶点、、上的高分別记作、、,則:
其中 。
角平分线长度
设在中,若三个角、、的角平分线分别为、、,则:
三角形的心
三角形的內心(Incenter) 、外心(Circumcenter)、垂心(Orthocenter) 及形心(Centroid)稱為三角形的四心,定義如下:
| 名称 | 定义 | 图示 | 备注 |
|---|---|---|---|
| 內心 | 三个內角的角平分线的交點 | 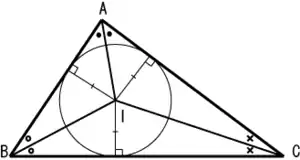 | 該點為三角形內切圓的圓心。 |
| 外心 | 三條邊的中垂線的交點 | 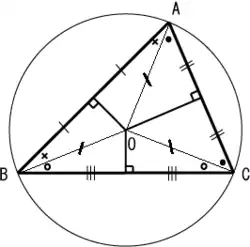 | 該點為三角形外接圓的圓心。 |
| 垂心 | 三条高线的交點 | 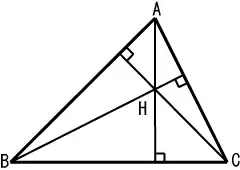 | |
| 形心(重心) | 三条中线的交點 | 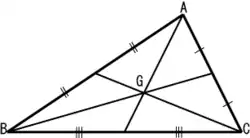 | 被交点划分的线段比例为1:2(靠近角的一段较长)。 |
关于三角形的四心,有这样的一首诗:
| 內心全靠角平分, 外心中點垂線伸, |
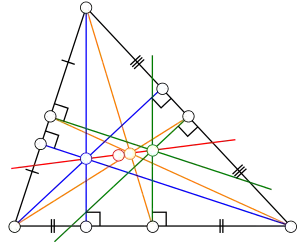
垂心(蓝)、形心(黄)和外心(绿)能連成一線,且成比例1:2,稱為歐拉線,與九點圓的圓心(紅)四點共線,為垂心和形心線段的中點。
連同以下的旁心,合稱為三角形的五心:
| 名称 | 定义 | 图示 | 备注 |
|---|---|---|---|
| 旁心 | 外角的角平分线的交點 | 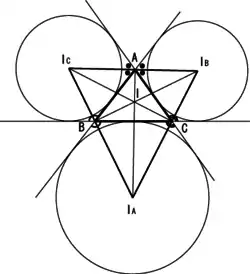 | 有三个,为三角形某一边上的旁切圆的圆心。 |
外接圆和内切圆半径
設外接圆半径為 , 内切圆半径為 ,則:
其中為三角形面積;為三角形半周長,
面積
基本公式
三角形的面積 是底邊 與高 乘積的一半,即:
- ,
其中的高是指底邊與對角的垂直距離。
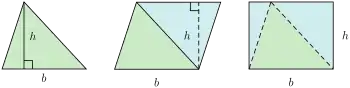
從右圖可知,將兩個全等三角形相拼,可得一平行四邊形。而將該平行四邊形分割填補,正好能得到一個面積等於 的長方形。因此原來的三角形面積為
- 。
證畢。
已知三邊長
海倫公式,其表示形式為:
- ,
其中 等於三角形的半周長,即:
秦九韶亦求過類似的公式,稱為三斜求積法:
也有用幂和来表示的公式:
亦可用Cayley–Menger行列式表示的公式:
基於海伦公式在三角形擁有非常小的角度時並不數值穩定,有一個變化的計法。設 ,三角形面積為:
- 。
已知坐标系中三顶点坐标
由 、 及 三个顶点构成的三角形,其面积可用行列式的絕對值表示:
无论三角形的顶点位置如何,该三角形总可以用一个直角梯形(或矩形)和两个直角三角形面积的和差来表示,而在直角坐标系中,已知直角梯形(或矩形)和直角三角形的顶点的坐标,该三角形的面积容易求出,即用上述的行列式表示。
若三個頂點設在三維坐標系上,即由 、 及 三个顶点构成三角形,其面積等於各自在主平面上投影面積的畢氏和,即:
已知周界及內切圓或外接圓半徑
設三角形三邊邊長分別為 、 及 ,三角形半周長( )為 ,內切圓半徑為 ,則:
若設外接圓半徑為 ,則:
其他有关三角形的定理
- 外角定理
- 拿破仑三角形
- 费马点
- 欧拉线
- 梅涅劳斯定理
- 樞紐定理
- 維維亞尼定理
- 莫雷角三分線定理
註釋
- 應用實例,如外森比克不等式的證明
參考資料
- P.F.Man,C.M.Yeung,K.H.Yeung,Y.F.Kwok,H.Y.Cheung,MATHEMATICS in Action SECOND EDITION 1B (Published by Longman Hong Kong Education): pp:9.25
- 黃德華. . 臺灣數學教師. 2016, 37 (2): 17–49 [2022-01-26]. doi:10.6610/TJMT.20160629.01. (原始内容存档于2022-01-26).
⋯⋯SSO(O 是一鈍角)也是判断全等三角形的正確條件
- Mironychev, Alexander F. . Journal of Mathematics and System Science. 2018, 8 (2): 59–66 [2022-01-26]. doi:10.17265/2159-5291/2018.02.003. (原始内容存档于2022-01-26).