六边形
在幾何學中,六邊形是指有六條邊和六個頂點的多邊形[1],其內角和為720度[2]。六邊形有很多種,其中對稱性最高的是正六邊形。正六邊形是一種可以使用尺規作圖的六邊形,也可以拼滿平面,因此自然界中可以找到許多正六邊形的結構,如蜂巢[3]、玄武岩[4]和苯的分子結構[5]。另外,正六邊形也可以構成一些高對稱性的多面體,如截角二十面體,巴克明斯特富勒烯的分子結構就是這種形狀。
| 正六邊形 | |
|---|---|
 一個正六邊形 | |
| 類型 | 正多邊形 |
| 對偶 | 正六邊形(本身) |
| 邊 | 6 |
| 頂點 | 6 |
| 對角線 | 9 |
| 施萊夫利符號 | {6} t{3} |
| 考克斯特符號 | |
| 對稱群 | 二面體群 (D6), order 2×6 |
| 面積 | |
| 內角(度) | 120° |
| 內角和 | 720° |
| 特性 | 凸、圓內接多邊形、等邊多邊形、等角多邊形、等邊圖形 |
六邊形依照其類角的性質可以分成凸六邊形和非凸六邊形,其中凸六邊形代表所有內角的角度皆小於180度。非凸六邊形可以在近一步分成凹六邊形和星形六邊形,其中星形六邊形表示邊自我相交的六邊形。
正六邊形
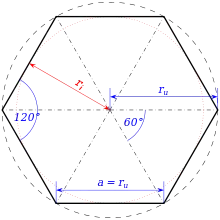
正六邊形是每條邊等長、每個角相等的六邊形,在施萊夫利符號中可以用來表示[6]。正六邊形亦可以將正三角形透過截角變換來構造,即切去正三角形的三個頂點,因此正六邊形在施萊夫利符號中亦可以寫為 。但若截角深度太深或太淺都會產生一種具有兩個不同邊長的六邊形。
正六邊形是一個同時具有邊可遞和點可遞特性的六邊形,是一種雙心多邊形,這意味著它同時具有內切圓和外接圓。
正六邊形邊的長度與其外接圓半徑相等,且等於邊心距的倍,其中,邊心距與內切圓半徑相等。正六邊形的每個內角都是120度,且具有6次的旋轉對稱性(階數為6的旋轉對稱性)和6軸對稱性(有6個對稱軸的軸對稱性),組成了D6二面體群的對稱性。正六邊形最長的對角線是兩側頂點的對角線,其長度恰好為邊長的兩倍,因此若有一個三角形其中一個頂點位於六邊形幾何中心、其中一條邊與六邊形共用,則這個三角形是正三角形,且正六邊形可以分割成6個此三角形。
正六邊形是其中一種能夠密鋪平面的正多邊形,其餘兩種為正三角形和正方形。如同正方形和正三角形一樣,正六邊形可以經過重複的排列和組合,形成沒有空隙或重疊的幾何圖形,這種圖行每個頂點都是3個六邊形的公共頂點,並形成一個很緊密的二維空間充填,也因此大部分的蜂窩都會將其的每個蜂房做成六邊形,使其能夠有效地利用空間和建材[3]。另外,正三角形鑲嵌的沃羅諾伊圖是正六邊形鑲嵌。雖然具有等邊的特性,但並不常被當作等邊多邊形。
正六边形尺规作图
下面是正六边形的尺规作图,共三步。

- 畫一條水平線,通過此線上的任意點做一個圓。
- 以該圓與線的交點为圆心,分別畫出與該圓半徑相同的圓,與該圓交於4點。
- 依顺序联结这4个点和該圓與水平線的交點即成正六邊形。
六邊形的密鋪平面
有多種六邊形可以獨立密鋪平面,換句話說即該六邊形反覆拼接可以無空隙地填滿整個平面[8][9]
| 對稱性 | p6m (*632) | cmm (2*22) | p2 (2222) | p31m (3*3) | pmg (22*) | pg (××) | |
|---|---|---|---|---|---|---|---|
| 圖形 |  r12 |
 i4 |
 g2 |
 d2 |
 d2 |
 p2 |
 a1 |
扭歪六邊形

扭歪六邊形,又稱不共面六邊形,是指頂點並非完全共面的六邊形
 立方體[10] |
 正八面體 |
皮特里多邊形
一些正扭歪六邊形來自於高维多胞體的皮特里多邊形。
| 4D | 5D | |
|---|---|---|
 三角三角柱體柱 |
 三角三角錐體錐 |
 正五胞體 |
自然中的六邊形
由於正六邊形具有高度對稱性,且可以無空隙地填滿整個平面,這種形狀稱為正六邊形鑲嵌,其頂點排佈稱為六邊形網格(英語:)[17]。以這些頂點為幾何中心的圓形可以構成二維空間中可能的圓形鑲嵌中最緊密的一種排佈[18],其牛頓數[19]為6[20][21],也因此自然界經常出現許多正六邊形的結構,例如蜂巢[3]、玄武岩[4]和一些化學物質的分子結構[5]。
在太空中,亦有其他自然形成的六邊形,例如土星極區的雲層呈現六邊形,被稱為土星六邊形。[22][23][24]


 龜殼
龜殼


 一些六方晶系礦物的結晶
一些六方晶系礦物的結晶 六角的雪花[28]
六角的雪花[28]
參考文獻
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- . coolmath.com. [2016-08-26]. (原始内容存档于2016-09-03) (英语).
- . [2016-08-26]. (原始内容存档于2020-10-16).
- 楊嵐雅. . 國立台灣大學. [2016-08-26]. (原始内容存档于2016-09-02).
- Rocke, A. J. . Angew. Chem. Int. Ed. 2015, 54: 46–50. doi:10.1002/anie.201408034.
- Wenninger, Magnus J., , Cambridge University Press: 9, 1974 [2016-08-25], ISBN 9780521098595, (原始内容存档于2016-01-02).
- 歐幾里得 《幾何原本》第四卷 第15章 BC 300
- Tilings and Patterns, Sec. 9.3 Other Monohedral tilings by convex polygons
- Tilings and Patterns, from list of 107 isohedral tilings, pp. 473–481
- ,Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, 1999. p. 170 ISBN 978-0486409146
- Gardner, M. "Mathematical Games: More About the Shapes that Can Be Made with Complex Dominoes." Sci. Amer. 203, 186-198, Nov. 1960.
- Holden, A. Shapes, Space, and Symmetry. New York: Dover, 1991. ISBN 978-0486268514
- Holden 1991[12], p.23
- Holden 1991[12], p.22-23
- Holden 1991[12], p.26-27
- Cundy, H. and Rollett, A. "Hexagonal Section of a Cube." §3.15.1 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 157, 1989. ISBN 978-0906212202
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- O. R. Musin. . Russ. Math. Surv. 2003, 58: 794–795. doi:10.1070/RM2003v058n04ABEH000651.
- . ifun01.com. [2017-07-10]. (原始内容存档于2021-10-15).
- Mittelmann, Hans D.; Vallentin, Frank. . Experimental Mathematics. 2009, 19: 174–178. arXiv:0902.1105
 .
. - See also Lemma 3.1 in Marathe, M. V.; Breu, H.; Hunt, H. B.; Ravi, S. S.; Rosenkrantz, D. J. . Networks. 1995, 25 (2): 59. doi:10.1002/net.3230250205.
- Godfrey, D.A. . Icarus. 1988, 76 (2): 335–356. Bibcode:1988Icar...76..335G. doi:10.1016/0019-1035(88)90075-9.
- Sanchez-Lavega, A.; Lecacheux, J.; Colas, F.; Laques, P. . Science. 1993, 260 (5106): 329–32. Bibcode:1993Sci...260..329S. PMID 17838249. S2CID 45574015. doi:10.1126/science.260.5106.329.
- Overbye, Dennis. . New York Times. August 6, 2014 [August 6, 2014]. (原始内容存档于2018-07-12).
- . NASA. 2007-03-27 [2017-07-10]. (原始内容存档于2010-02-01).
- . NASA. 2007-03-27 [2017-07-10]. (原始内容存档于2010-09-27).
- Godfrey, D. A. 76. Icarus: 335–356. 1988-11 [2020-09-30]. ISSN 0019-1035. doi:10.1016/0019-1035(88)90075-9. (原始内容存档于2017-08-09).
- Kepler, Johannes. [The Six-sided Snowflake]. Oxford: Clarendon Press. 1966 [1611]. OCLC 974730.