The Socolar–Taylor tile is a single non-connected tile which is aperiodic on the Euclidean plane, meaning that it admits only non-periodic tilings of the plane (due to the Sierpinski's triangle-like tiling that occurs), with rotations and reflections of the tile allowed.[1] It is the first known example of a single aperiodic tile, or "einstein".[2] The basic version of the tile is a simple hexagon, with printed designs to enforce a local matching rule, regarding how the tiles may be placed.[3] It is currently unknown whether this rule may be geometrically implemented in two dimensions while keeping the tile a connected set.[2][3]
This is, however, confirmed to be possible in three dimensions, and, in their original paper, Socolar and Taylor suggest a three-dimensional analogue to the monotile.[1] Taylor and Socolar remark that the 3D monotile aperiodically tiles three-dimensional space. However the tile does allow tilings with a period, shifting one (non-periodic) two dimensional layer to the next, and so the tile is only "weakly aperiodic".
Physical copies of the three-dimensional tile could not be fitted together without allowing reflections, which would require access to four-dimensional space.[2][4]
Gallery
The monotile implemented geometrically. Black lines are included to show how the structure is enforced.
A three-dimensional analogue of the Socolar-Taylor tile (all matching rules implemented geometrically)
A three-dimensional analogue of the monotile, with matching rules implemented geometrically. Red lines are included only to illuminate the structure of the tiling. Note that this shape remains a connected set.
A partial tiling of three-dimensional space with the 3D monotile.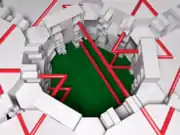
A tiling of 3D space with one tile removed to demonstrate the structure.
References
- 1 2 Socolar, Joshua E. S.; Taylor, Joan M. (2011), "An aperiodic hexagonal tile", Journal of Combinatorial Theory, Series A, 118 (8): 2207–2231, arXiv:1003.4279, doi:10.1016/j.jcta.2011.05.001, MR 2834173.
- 1 2 3 Socolar, Joshua E. S.; Taylor, Joan M. (2012), "Forcing nonperiodicity with a single tile", The Mathematical Intelligencer, 34 (1): 18–28, arXiv:1009.1419, doi:10.1007/s00283-011-9255-y, MR 2902144
- 1 2 Frettlöh, Dirk. "Hexagonal aperiodic monotile". Tilings Encyclopedia. Retrieved 3 June 2013.
- ↑ Harriss, Edmund. "Socolar and Taylor's Aperiodic Tile". Maxwell's Demon. Retrieved 3 June 2013.
External links
- Previewable digital models of the three-dimensional tile, suitable for 3D printing, at Thingiverse
- Original diagrams and further information on Joan Taylor's personal website
