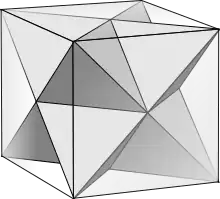
半刻面立方體
在幾何學中,半刻面立方體(英語:)是一種非凸多面體,由立方體刻面而成[1],換句話說即不更動立方體的頂點,將立方體的面替換為對角面構成,並補上適當的表面之面,使立體成為封閉的多面體[2]。由於半刻面立方體有部分的面幾何中心落在整個立體的幾何中心上,因此其又可以歸類為半多面體[3],也因此這個多面體的對偶多面體的頂點會落在無窮遠處,即無窮实射影平面上的點[4]。特別地,這個多面體的五複合體的對偶多面體是一種星形二十面體,但由於其頂點落在無窮实射影平面而並未收錄於《五十九種二十面體》中,因此被描述為「遺失的星形二十面體」[5][6]。
 () | |||
| 類別 | 非凸多面體 | ||
|---|---|---|---|
| 性質 | |||
| 面 | 12 | ||
| 邊 | 24 | ||
| 頂點 | 8 | ||
| 歐拉特徵數 | F=12, E=24, V=8 (χ=-4) | ||
| 組成與佈局 | |||
| 頂點圖 | 星形六邊形[1] | ||
| 對稱性 | |||
| 對稱群 | Oh, [4,3], (*432) | ||
| 圖像 | |||
| |||
性質
半刻面立方體由12個面、24條邊和8個頂點組成,其中6個面為立方體的對角面,6個面為立方體原始的面轉為折四邊形的結果。[1][7]
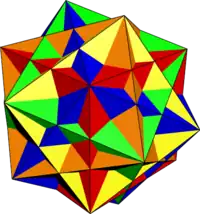
五複合半刻面立方體
 五複合立方體,每個半刻面立方體以不同顏色表示 | |
| 類別 | 複合多面體 |
|---|---|
| 對偶多面體 | 五複合立方半無窮星形菱形六十面體 |
| 性質 | |
| 體 | 5 |
| 面 | 60 |
| 邊 | 120 |
| 頂點 | 20 |
| 歐拉特徵數 | F=60, E=120, V=20 (χ=-40) |
| 組成與佈局 | |
| 複合幾何體數量 | 5 |
| 複合幾何體種類 | 五個半刻面立方體 |
| 面的種類 | 30個長方形 30個反平行四邊形 |
| 對稱性 | |
| 對稱群 | 二十面體群 (Ih) |
五複合半刻面立方體是由半刻面立方體通過立方體合成五複合立方體的方式組成的幾何結構。[5]其也可以視為是正十二面體的刻面多面體[9]。
構成方式
由半刻面立方體建構五複合半刻面立方體的方式,與由立方體構造成五複合立方體的方式一樣。[5]即可透過將一個半刻面立方體以原點為中心、面向軸的第一個半刻面立方體開始構造,其餘的半刻面立方體則透過軸旋轉弧度來構造,並依這加入順序決定角度值中的n,例如第二個半刻面立方體對應n=1、第三個半刻面立方體對應n=2,以此類推。[10]
五複合半刻面立方體的對偶多面體
 (點選檢視3D模型) | ||||||||||||
| 類別 | 星形二十面體 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 對偶多面體 | 五複合半刻面立方體 | |||||||||||
| 性質 | ||||||||||||
| 體 | 5 | |||||||||||
| 面 | 20 | |||||||||||
| 邊 | 120 | |||||||||||
| 頂點 | 60 | |||||||||||
| 歐拉特徵數 | F=20, E=120, V=60 (χ=-40) | |||||||||||
| 組成與佈局 | ||||||||||||
| 複合幾何體數量 | 5 | |||||||||||
| 複合幾何體種類 | 5個半刻面立方體的對偶多面體 | |||||||||||
| 面的種類 | (由無窮实射影平面上的點構成) | |||||||||||
| 對稱性 | ||||||||||||
| 對稱群 | 二十面體群 (Ih) | |||||||||||
| 圖像 | ||||||||||||
| ||||||||||||
由於五複合半刻面立方體有部分面幾何中心落在整個立體的幾何中心上,因此其對偶多面體的頂點會落在無窮遠處,即無窮实射影平面上的點[3][4]。為了具像化這種立體,溫尼爾在著作《對偶模型》中將其描述為由無限高的柱體組合構成的立體[4][5]。特別地,這個多面體是一種星形多面體,但由於其頂點落在無窮实射影平面而並未收錄於《五十九種二十面體》中,因此被描述為「遺失的星形二十面體」[5]。
 五複合半刻面立方體的對偶多面體 |
 完全星形二十面體 |
 五複合半刻面立方體 |
 五複合半刻面立方體(黃色)與五複合半刻面立方體的對偶多面體(藍色)的複合體 |
- 作為星形多面體
五複合半刻面立方體的對偶多面體可以看作是一種正二十面體的星形多面體[5],其在杜瓦記號中可以用hj2表示[5]。
| 星狀圖 | 星形 | 星狀核 | 凸包 |
|---|---|---|---|
 |
 |
 正二十面體 |
(無法具象化) |
相關多面體
其他由立方體的頂點構成,但邊或面連結方式與立方體相異的立體有:
 立方體 |
 半刻面立方體 |
 星形八面體 |
 皮特里立方體 |
這個立體為柏拉圖立體半刻面後而成,其他也由柏拉圖立體半刻面而成的立體有:[1]
 正四面體 |
 立方體 |
 正八面體 |
| (無「半刻面」的結果) |  半刻面立方體 |
 半刻面八面體 |
皮特里立方體
 以不同顏色表示每個面 | |
| 類別 | 皮特里對偶 正則地區圖 |
|---|---|
| 對偶多面體 | {3,6}(2,2) |
| 數學表示法 | |
| 施萊夫利符號 | {4,3}π {6,3}(2,2)[12] {6,3}2,0[14] |
| 性質 | |
| 面 | 4 |
| 邊 | 12 |
| 頂點 | 8 |
| 歐拉特徵數 | F=4, E=12, V=8 (χ=0) |
| 二面角 | (不存在) |
| 對稱性 | |
| 對稱群 | Oh, [4,3], (*432) |
| 特性 | |
| 扭歪、正則 | |
皮特里立方體是立方體的皮特里對偶,可以透過將原有立方體上取皮特里多邊形構成,換句話說,皮特里立方體為由立方體的皮特里多邊形構成的立體[11]。由於立方體的皮特里多邊形為扭歪六邊形,因此無法確立其封閉範圍,故無法計算其表面積和體積。
皮特里立方體是一個可定向且歐拉示性數為零的幾何結構[12]。皮特里立方體共有4個面、12條邊和8個頂點。其中面由4個扭歪六邊形面組成,每個頂點都是3個扭歪六邊形的公共頂點。[12]
 立方體的皮特里多邊形 |
 構成皮特里立方體的扭歪六邊形面 |
皮特里立方體與立方體互為皮特里對偶,也就是說,皮特里立方體的皮特里對偶為立方體,換句話說,即皮特里立方體的皮特里多邊形為正方形[12][15]。皮特里立方體可以截半為八面半八面體[12][16]。
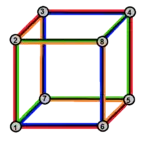 皮特里立方體 |
 以正則地區圖表示的皮特里立方體 |
 皮特里立方體的對偶多面體以正則地區圖表示[17] |
參見
參考文獻
- Inchbald, Guy. . The Mathematical Gazette (Cambridge University Press). 2006, 90 (518): pp. 253–261. doi:10.1017/S0025557200179653.
- Inchbald, Guy. . Jms. 29 July 2004, 30: 30 [2021-07-24]. (原始内容存档于2021-06-08).
- Hart, George. . Virtual Polyhedra: The Encyclopedia of Polyhedra. 1996 [6 May 2012]. (原始内容存档于2021-07-24).
- Wenninger, Magnus, , Cambridge University Press, 2003 [1983], ISBN 978-0-521-54325-5, MR 0730208, doi:10.1017/CBO9780511569371 (Page 101, Duals of the (nine) hemipolyhedra)
- Guy's polyhedra pages. . steelpillow. 2006-07-11 [2016-09-01]. (原始内容存档于2016-03-13). Index Number: 303, Precursor: BnGn, Du Val symbol: De2f2
- G. Inchbald, In search of the lost icosahedra, Math. Gaz. 86 (July 2002) pp. 208-215.
- Robert Webb. . www.software3d.com.
- . dmccooey.com. [2021-07-24]. (原始内容存档于2021-07-24).
- Inchbald, G. . Symmetry: Culture and Science. 2000, 11: 1––4 [2021-07-29]. (原始内容存档于2021-06-08).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Gorini, Catherine A., , MAA Notes 53, Cambridge University Press: 181, 2000, ISBN 9780883851647
- . Regular Map database - map details. [2021-07-24].
- Coxeter, H. S. M.; Moser, W. O. J., , Ergebnisse der Mathematik und ihrer Grenzgebiete 14 4th, Springer Verlag, 1980, ISBN 978-0-387-09212-6
- Coxeter 1980[13], 8.4 Maps of type {3,6} or {6,3} on a torus.
- . Regular Map database - map details. [2021-07-30]. (原始内容存档于2020-02-01).
- . Regular Map database - map details. [2021-07-24]. (原始内容存档于2021-07-25).
- . Regular Map database - map details. [2021-07-24].